算法day12-二叉树（2）

目录

1. 二叉树的最大深度
2. 二叉树的最小深度
3. 扩展题

一、二叉树的最大深度

　　https://leetcode.cn/problems/maximum-depth-of-binary-tree?envType=problem-list-v2&envId=8At1GmaZ

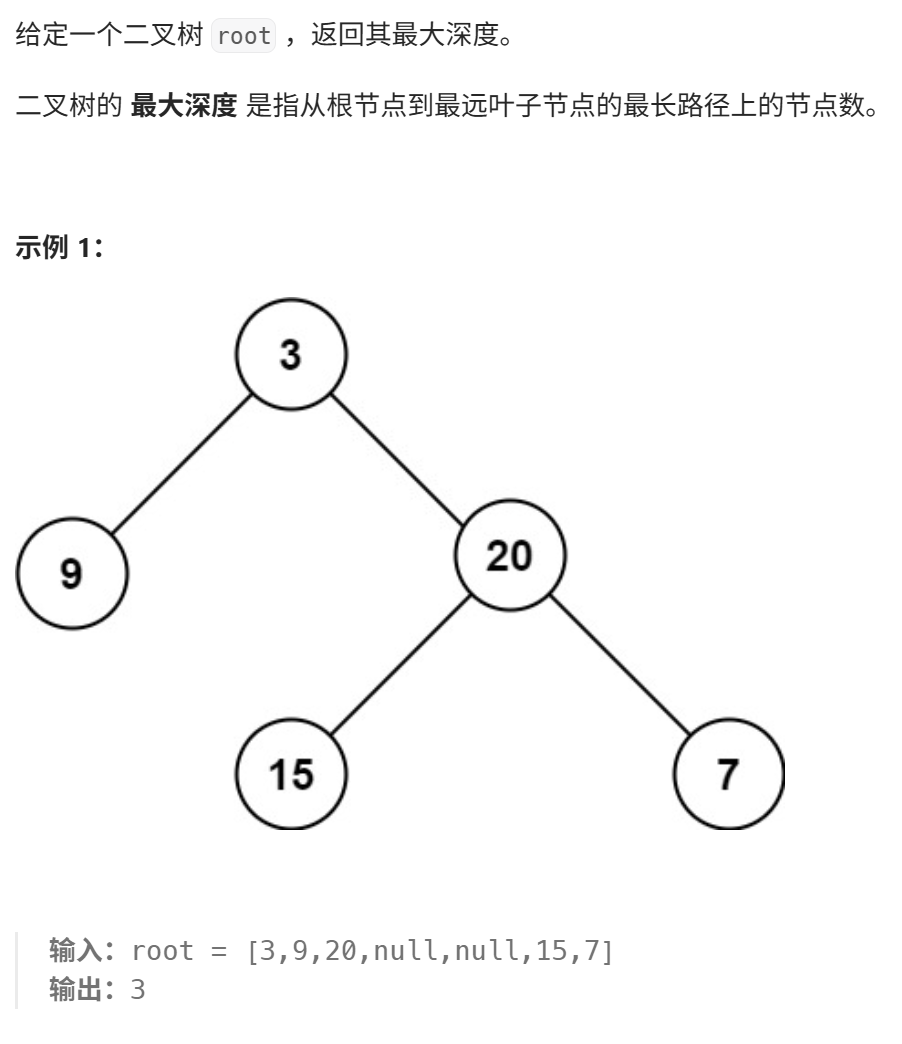
 　　这道题可以用广度优先搜索/深度优先方法做。

1. 深度优先遍历（递归）

class Solution{
    public int maxDepth(TreeNode root) {
        if(root == null){
            return 0;
        }
        int leftDepth = maxDepth(root.left);
        int rightDepth = maxDepth(root.right);

        return Math.max(leftDepth, rightDepth) + 1;
    }
}

      1
     / \
    2   3
   /
  4

递归展开过程：
maxDepth(1)
  → maxDepth(2)
      → maxDepth(4)
          → maxDepth(null) → return 0
          → maxDepth(null) → return 0
          → return max(0, 0) + 1 = 1
      → maxDepth of node 4 = 1
      → maxDepth(null) → return 0
      → return max(1, 0) + 1 = 2
  → maxDepth of node 2 = 2

  → maxDepth(3)
      → maxDepth(null) → return 0
      → maxDepth(null) → return 0
      → return max(0, 0) + 1 = 1
  → maxDepth of node 3 = 1

→ return max(2, 1) + 1 = 3

2. 广度优先遍历

class Solution {
    public int maxDepth(TreeNode root) {
        int depth = 0;
        if(root == null){
            return 0;
        }
        Queue<TreeNode> queue = new LinkedList<>();
        queue.offer(root);
        
        while(!queue.isEmpty()){
            int size = queue.size();
            for(int i=0; i<size; i++){
                TreeNode cur = queue.poll();
                if(cur.left != null)    queue.offer(cur.left);
                if(cur.right != null)   queue.offer(cur.right);
            }
            depth++;
        }
        return depth;
    }
}

二、二叉树的最小深度

　　https://leetcode.cn/problems/minimum-depth-of-binary-tree?envType=problem-list-v2&envId=8At1GmaZ

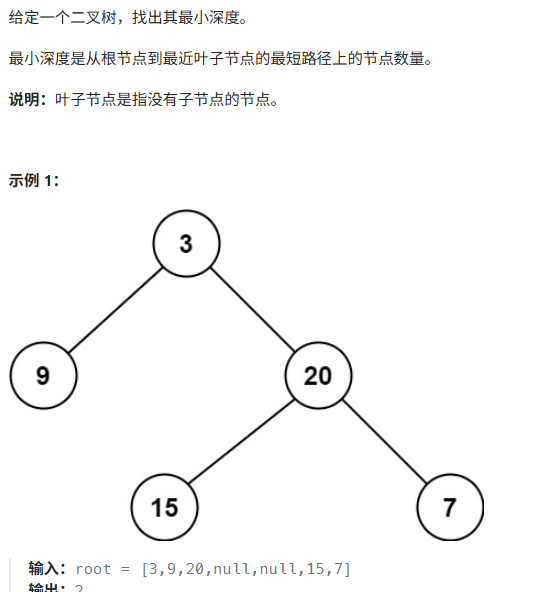
 　　这道题求最短路径，用BFS，遇到第一个叶子节点就返回深度即可。

class Solution {
    public int minDepth(TreeNode root) {
        if(root == null){
            return 0;
        }
        Queue<TreeNode> queue = new LinkedList<>();
        queue.offer(root);
        int depth = 0;
        while(!queue.isEmpty()){
            depth++;
            int size = queue.size();
            for(int i=0; i<size; i++){
                TreeNode cur = queue.poll();
                if(cur.left == null && cur.right == null){
                    return depth;
                }
                if(cur.left != null)    queue.offer(cur.left);
                if(cur.right != null)   queue.offer(cur.right);
            }
        }
        return depth;
    }   
}

 三、扩展题（都是BFS的扩展题）

1. 二叉树的右视图

　　https://leetcode.cn/problems/binary-tree-right-side-view/?envType=problem-list-v2&envId=8At1GmaZ

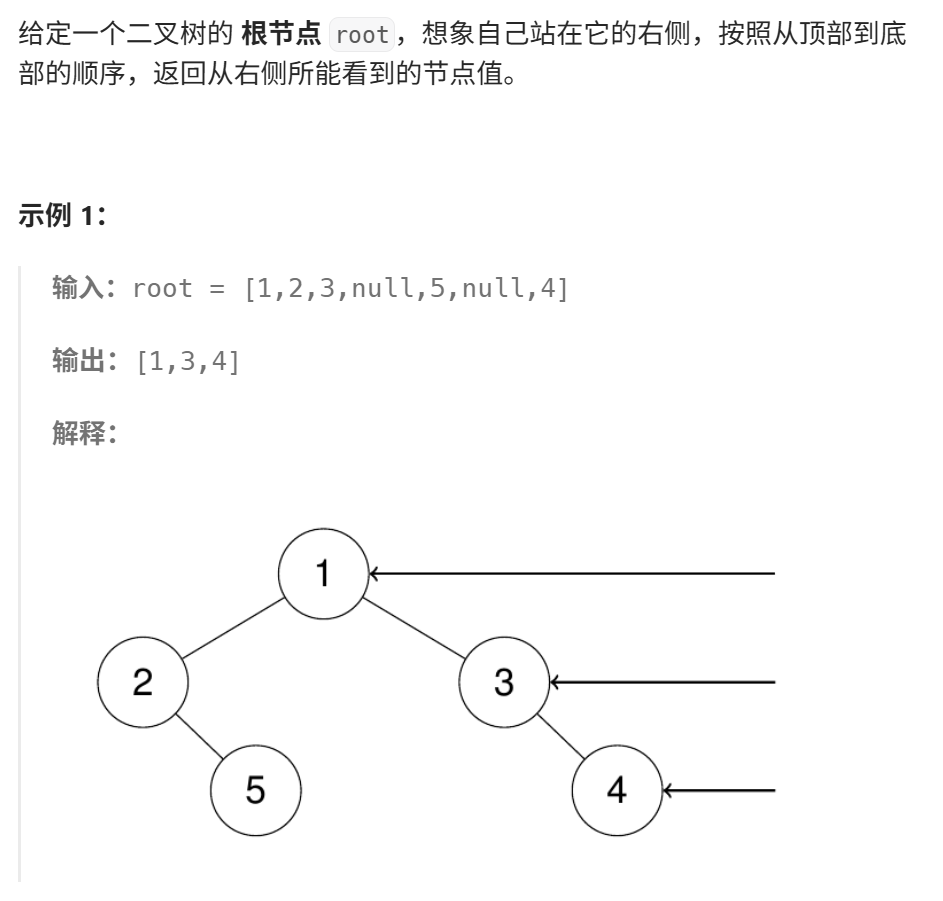
 　　这道题可以用BFS来做，也就是当层序遍历到每一层的最后一个节点时，将这个节点加入结果即可。

class Solution {
    public List<Integer> rightSideView(TreeNode root) {
        List<Integer> res = new ArrayList<>();
        if(root == null){
            return res;
        }
        Queue<TreeNode> queue = new LinkedList<>();
        queue.offer(root);
        while(!queue.isEmpty()){
            int size = queue.size();
            for(int i = 0; i<size; i++){
                TreeNode cur = queue.poll();
                if(i == size-1){
                    res.add(cur.val);
                }
                if(cur.left != null)    queue.offer(cur.left);
                if(cur.right != null)   queue.offer(cur.right);
            }
        }
        return res;
    }
}

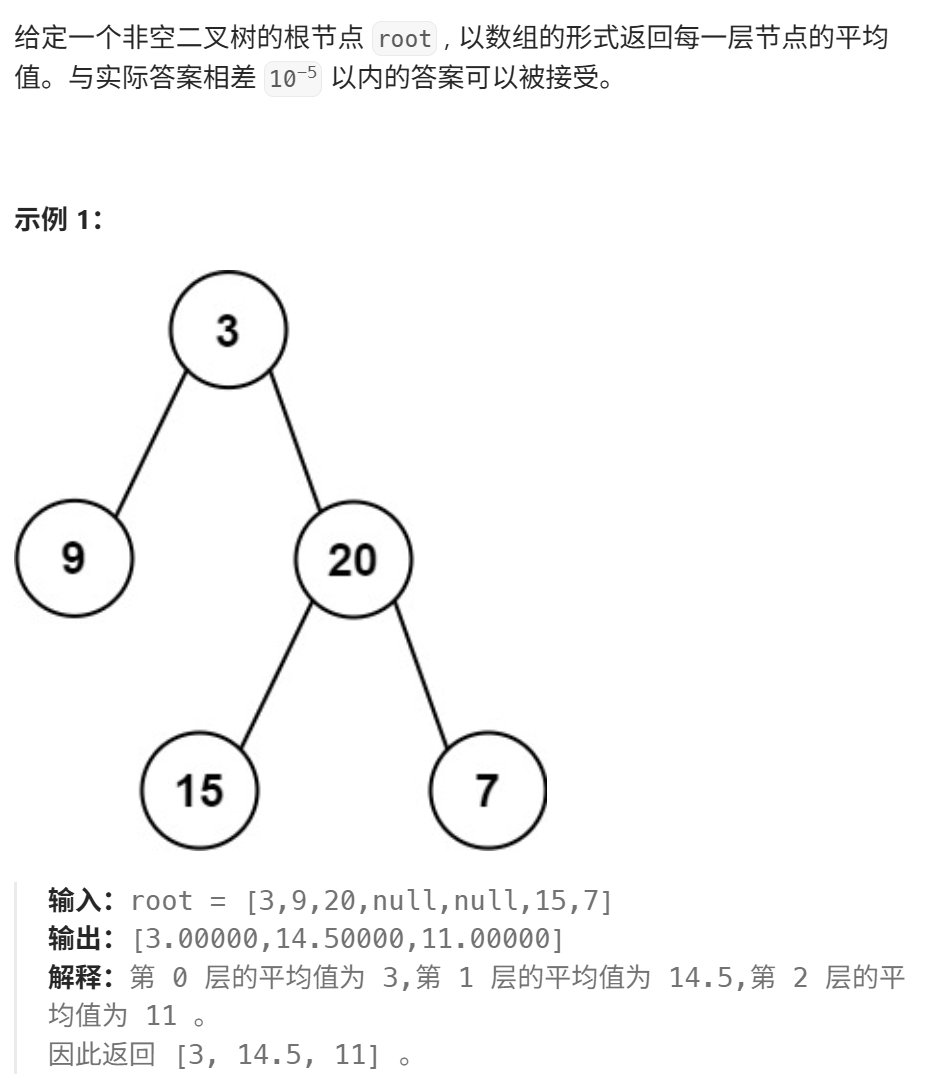
2. 二叉树的层平均值

　　https://leetcode.cn/problems/average-of-levels-in-binary-tree/description/?envType=problem-list-v2&envId=8At1GmaZ

class Solution {
    public List<Double> averageOfLevels(TreeNode root) {
        List<Double> res = new ArrayList<>();
        if(root == null){
            return res;
        }
        Queue<TreeNode> queue = new LinkedList<>();
        queue.offer(root);
        Double sum = 0.00;
        Double avg = 0.00;
        while(!queue.isEmpty()){
            sum = 0.00;
            avg = 0.00;
            int size = queue.size();
            for(int i=0; i<size; i++){
                TreeNode cur = queue.poll();
                sum += cur.val;
                if(cur.left != null)    queue.offer(cur.left);
                if(cur.right != null)   queue.offer(cur.right);
            }
            avg = sum / size;
            res.add(avg);
        }
        return res;
    }
}

3. N叉树的层序遍历

　　https://leetcode.cn/problems/n-ary-tree-level-order-traversal/?envType=problem-list-v2&envId=8At1GmaZ

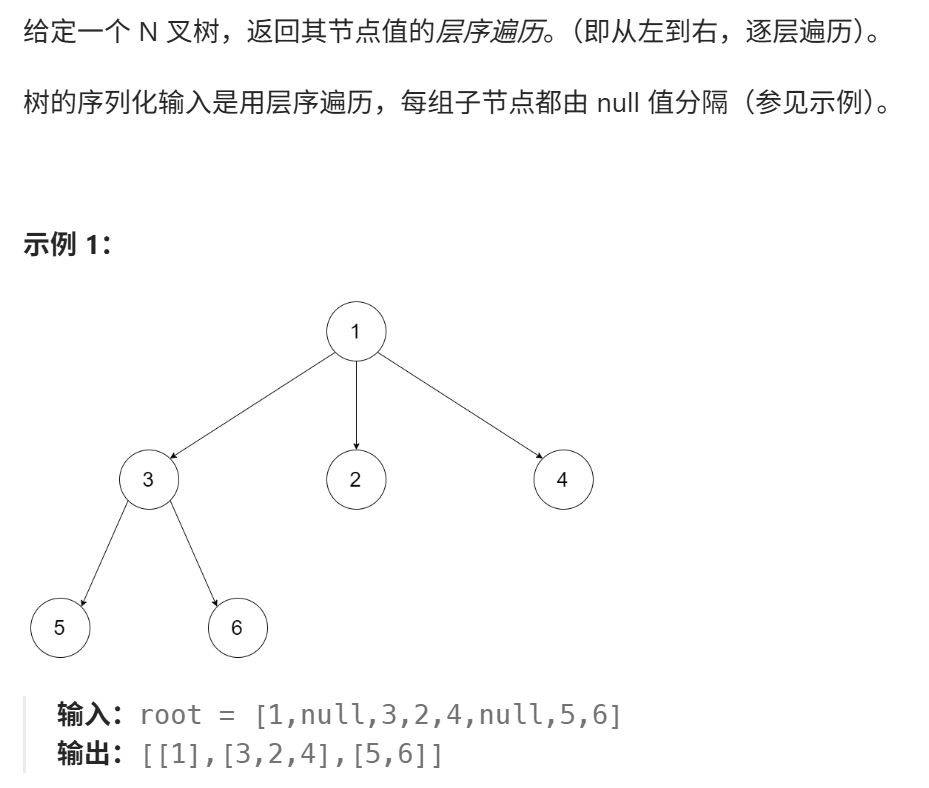
class Node {
    public int val;
    public List<Node> children;

    public Node() {}

    public Node(int _val) {
        val = _val;
    }

    public Node(int _val, List<Node> _children) {
        val = _val;
        children = _children;
    }
};

class Solution {
    public List<List<Integer>> levelOrder(Node root) {
        List<List<Integer>> res = new ArrayList<>();
        if(root == null){
            return res;
        }
        Queue<Node> queue = new LinkedList<>();
        queue.offer(root);
        while(!queue.isEmpty()){
            List<Integer> level = new ArrayList<>();
            int size = queue.size();
            for(int i=0; i<size; i++){
                Node cur = queue.poll();
                level.add(cur.val);
                for(Node node : cur.children){
                    queue.offer(node);
                }
            }
            res.add(level);
        }
        return res;
    }
}

4. 在每个树行中找最大值

　　https://leetcode.cn/problems/populating-next-right-pointers-in-each-node/description/?envType=problem-list-v2&envId=8At1GmaZ

 

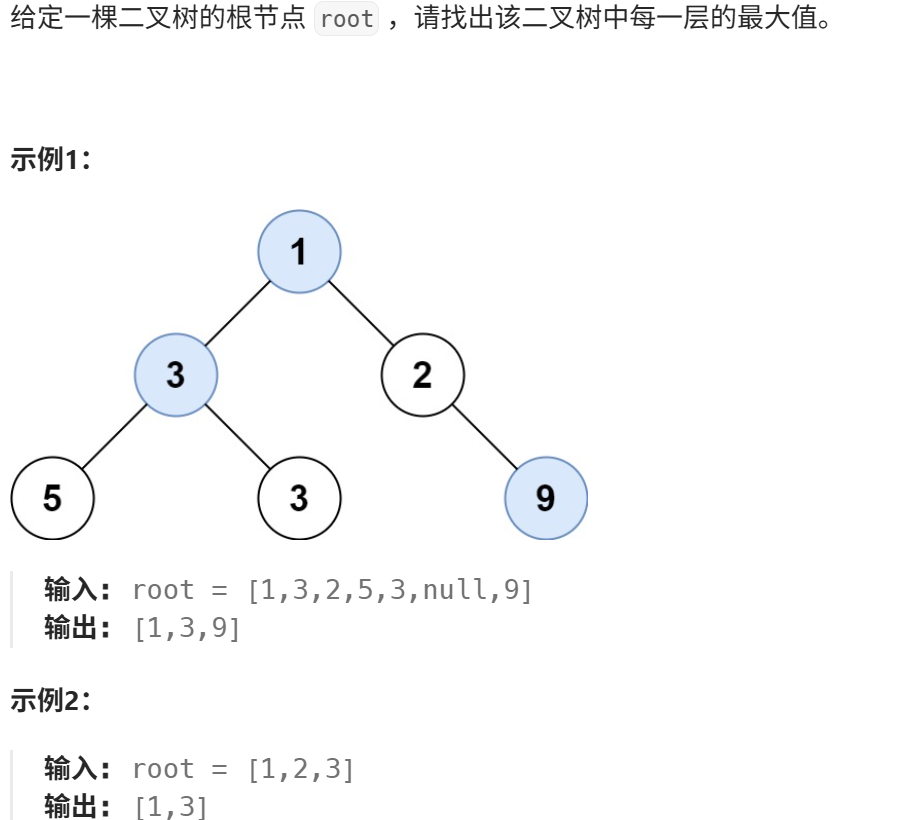
class Solution {
    public List<Integer> largestValues(TreeNode root) {
        List<Integer> res = new ArrayList<>();
        if(root == null){
            return res;
        }
        Queue<TreeNode> queue = new LinkedList<>();
        queue.offer(root);
        int maxLevel = Integer.MIN_VALUE;
        while(!queue.isEmpty()){
            maxLevel = Integer.MIN_VALUE;
            int size = queue.size();
            for(int i = 0; i < size; i++){
                TreeNode cur = queue.poll();
                maxLevel = Math.max(maxLevel, cur.val);
                if(cur.left != null)    queue.offer(cur.left);
                if(cur.right != null)   queue.offer(cur.right);
            }
            res.add(maxLevel);
        }
        return res;
    }
}

 

5. 填充每个节点的下一个右侧节点指针

　　https://leetcode.cn/problems/populating-next-right-pointers-in-each-node?envType=problem-list-v2&envId=8At1GmaZ

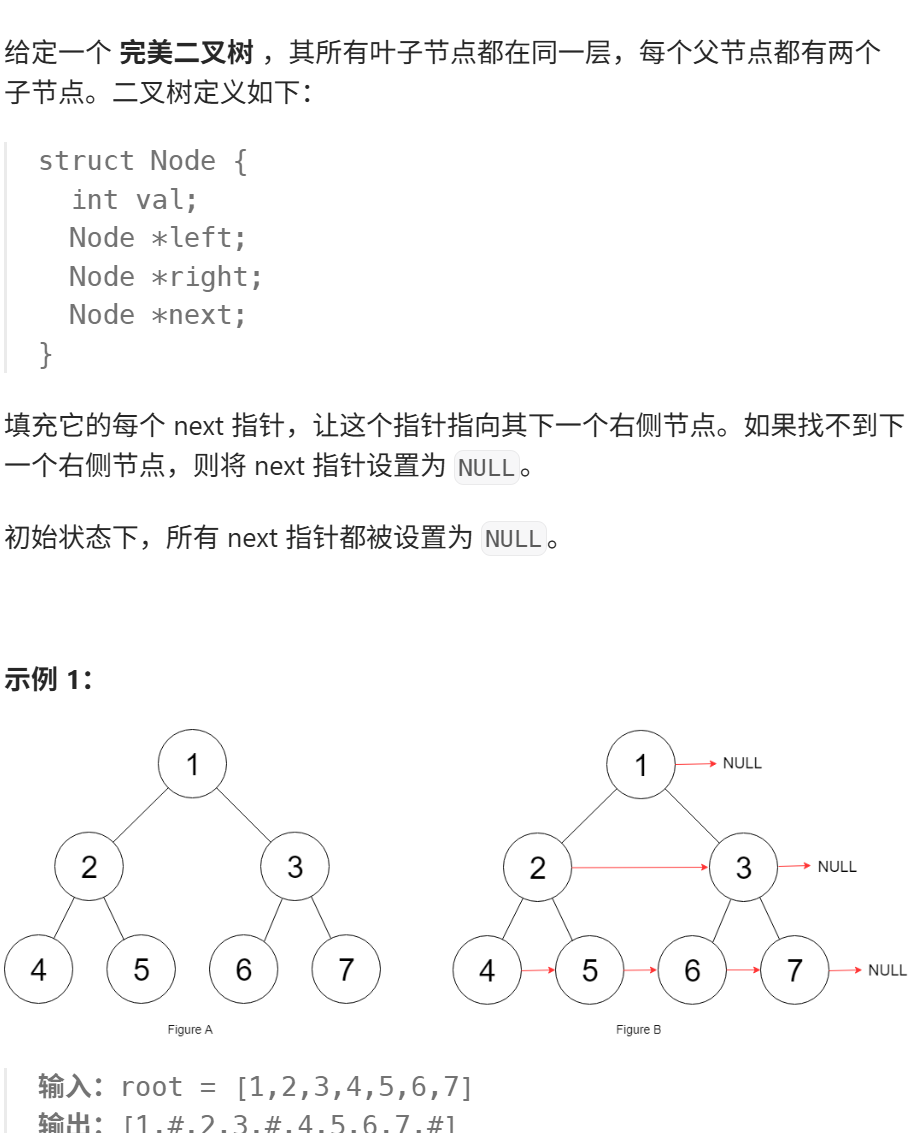
　　主要思路： 这段代码使用层序遍历（BFS）的方法，通过队列按层访问二叉树的每个节点，在每层中依次将节点的 next 指针指向其右侧的节点（即队列中的下一个节点），如果是该层的最后一个节点则指向 null，同时将左右子节点加入队列，用于处理下一层。该方法可用于普通二叉树，时间复杂度为O(N)。

/*
// Definition for a Node.
class Node {
    public int val;
    public Node left;
    public Node right;
    public Node next;

    public Node() {}
   
    public Node(int _val) {
        val = _val;
    }

    public Node(int _val, Node _left, Node _right, Node _next) {
        val = _val;
        left = _left;
        right = _right;
        next = _next;
    }
};
*/

class Solution {
    public Node connect(Node root) {
        if(root == null){
            return root;
        }
        Queue<Node> queue = new LinkedList<>();
        queue.offer(root);
        while(!queue.isEmpty()){
            int size = queue.size();
            for(int i =0; i<size; i++){
                Node cur = queue.poll();
           
                if(i == size-1){
                    cur.next = null;
                }else{
                    cur.next = queue.peek();
                }
                if(cur.left!=null)  queue.offer(cur.left);
                if(cur.right != null)   queue.offer(cur.right);
            }
        }
        return root;
    }
}

6. 填充每个节点的下一个右侧节点

 　　代码同上。