SVM支持向量机 Support Vector Machines

简介

支持向量机是一种二分类模型，它的学习策略就是间隔最大化，可形式化为一个求解凸二次规划(convex quadratic programming)的问题

线性可分支持向量机

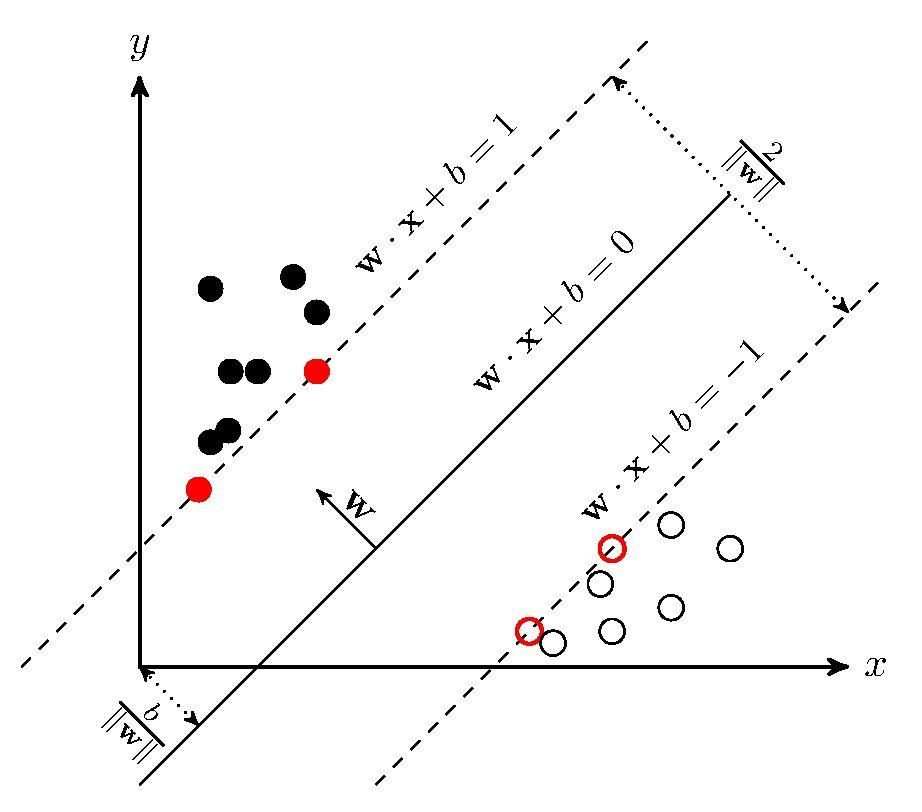
假设给定特征空间上的训练数据集

\[T={(x_1,y_1),(x_2,y_2),\cdots,(x_N,y_N)} \]

其中\(x_i \in \R^n, \ y_i \in {+1,-1}\)且数据集是线性可分的

学习的目标是找到一个分离超平面\(w\cdot x+b=0\),能将实例分到不同的类。法向量\(w\)指向的一侧为正类,另一侧为负类。

函数间隔 functional margin

对于超平面\(w\cdot x+b=0\), \(\frac {|w\cdot x+b|} {||w||}\)表示点\(x\)距离超平面的距离,而\(w\cdot x+b\) 的符号与\(y\)符号是否一致能够表示分类是否正确,所以可以用\(y(w\cdot x+b)\)来表示分类的正确性,这就是函数间隔

对于给定训练数据集\(T\)和超平面\((w,b)\),定义超平面\((w,b)\)关于样本点\((y_i,x_i)\)的函数间隔为

\[\tilde \gamma_i=y_i(w\cdot x_i+b) \]

如果成比例地改变\(w\)和\(b\)，例如将它们改成\(2w\)和\(2b\)，超平面并没有改变,但函数间隔变为了原来的2倍。所以我们可以对法向量\(w\)加一些约束，使得间隔是确定的，此时的函数间隔成为几何间隔

几何间隔 geometric margin

\[\gamma_i=y_i(\frac {w} {||w||_2}\cdot x_i+\frac {b} {||w||_2}) \]

函数最大化

\[\begin{align*} &\max_{w,b} \gamma\\ &s.t. y_i(\frac {w} {||w||}\cdot x_i+\frac {b} {||w||} \ge \gamma \end{align*} \]

转化为间隔函数的形式

\[\begin{align*} &\max_{w,b} \frac {\tilde \gamma} {||w||}\\ &s.t. y_i(w \cdot x_i+b) \ge \tilde \gamma \end{align*} \]

函数间隔的取值不影响最优化问题的解,这样就可以取\(\tilde \gamma=1\)，最大化\(\frac 1 {||w||}\)和最小化\(\frac 1 2 ||w||^2\)等价
于是就得到了线性可分支持向量机学习的最优化问题

\[\begin{align*} &\min_{w,b} \frac 1 2 ||w||^2\\ &s.t. y_i(w \cdot x_i+b)-1 \ge 0 \end{align*} \]

这是一个凸二次规划问题
假设通过间隔最大化得到的分离超平面为

\[w^*\cdot x+b^*=0 \]

相应的分类决策函数为

\[f(x)={\rm sign} (w^*\cdot x+b^*) \]

支持向量

训练样本数据集的样本点中与分离超平面距离最近的样本点的实例称为支持向量,是使约束条件等号成立的点,即

\[y_i(w\cdot x_i+b)-1=0 \]

对偶问题

拉格朗日函数形式

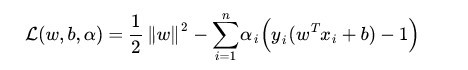
然后令

\[\theta(w)=\max_{a_i \ge 0}\mathcal L(w,b,a)\\ \theta(w)= \begin{cases} \frac 1 2 ||w||^2 &x \in 可行域\\ \infty &x \notin 可行域 \end{cases} \]

原问题为

化为拉格朗日对偶问题

条件约束

推导过程看这篇博客

最后得到

\[\begin{align*} \min_a \ &\frac 1 2 \sum_{i,j=1}^N a_ia_jy_iy_j{x_i}^Tx_j-\sum_{i=1}^N a_i\\ s.t. \ &\sum_{i=1}^Na_iy_i=0\\ &a_i \ge 0 \end{align*} \]

分类决策函数为

\[f(x)={\rm sign}\left(\sum_{i=1}^N{a_i}^*y_i(x^Tx_i)+b^*\right) \]

Reference

[1]《统计学习方法》 李航
[2] https://zhuanlan.zhihu.com/p/31886934