面试进阶算法之六(未排序数组累加和问题,环形单链表的约瑟夫问题,字符串匹配问题)
题目一:
给定一个数组arr,全是正数;一个整数aim,求累加和等 于k的,最长子数组,要求额外空间复杂度O(1),时间 复杂度O(N)
例如:arr[1,2,1,1,1] ,k =3
累加和为3的最长子数组为[1,1,1],所以结果返回3
思路:这类问题一般是用双指针来解决,用2个位置来标记子数组的左右两头,计作left,right,开始的时候,都在数组的最左边。过程如下:
1 开始的时候left=0,right=0 ,代表子数组arr[left..right]
2 变量sum 表示 arr[left..right] 的累加和
3 变量len一直记录累加和为k的所有子数组中最大子数组的长度。开始 len=0
4 根据sum和k的比较结果决定是left移动还是right移动。具体如下:
1如果sum<k,说明right需要继续向后移动 ,才能使 和 可能为k,所以 right+1,sum = sum+arr[right].需要注意,right+1之后是否越界
2 sum==k,找到了我们需要的结果,更加当前的len更新新的len。因为当前数组中全为正数,所以所有从left位置开始,在right位置之后的位置 结束的子数组,即
arr[left..i(i>right)],累加和一定大于k。所以我们让left加1,表示我们开始考察以left之后的位置开始的子数组,同时令sum-=arr[left],sum此时表示 arr[left+1..right]的累加和
3 sum>k, 和条件2是一个套路
因为当前数组中全为正数,所以所有从left位置开始,在right位置之后的位置 结束的子数组,即
arr[left..i(i>right)],累加和一定大于k。所以我们让left加1,表示我们开始考察以left之后的位置开始的子数组,同时令sum-=arr[left],sum此时表示 arr[left+1..right]的累加和
结束条件:right>=arr.length.也就是right指针到达最右边的时候,终止
疑问1: 这种遍历套路是否会 丢失调最优解。
答案:不会。我们可以这么理解。left指针指向的地方表示以left位置开头的 和为k的最大子数组的长度,left+1表示以left+1位置开头的和为k的最大子数组的长度。
如果求出left开头的最大子数组长度,right指针就不需要继续往右,因为都是正数,继续往右必大于k,所以left+1,开始下一个开头的统计。
疑问2:为什么right到达最右边就可以终止
比如
情况1 left当前到达 m的位置,right到达 arr.length-1的位置,此时元素和为k,那么left就不需要往右再走了,因为再走肯定小于k了,不是我们需要的
情况2 left到达m的位置,right到达 arr.length-1的位置,此时元素的和小于k,left继续走的话,也还是小于k,所以可以终止
情况3 left到达m的位置,right到达 arr.length-1的位置,此时元素的和大于k,此时left可以继续向右走,right不动,那么left总会达到 情况1和情况2的情况,此时 终止
代码:
int getMaxLength(vector<int>&arr,int k){ if(arr.size()==0||k<=0){ return 0; } int left=0; int right=0; int sum = arr[0]; int len = 0; while (right<arr.size()) { if(sum == k){ len = max(len, right-left+1); sum -= arr[left]; left++; //left 向右括 } else if(sum<k){ right++;//right 向右括 if(right==arr.size()){ break; } sum += arr[right]; } else { sum -= arr[left]; left++; //left 向右括 } } return len; }
题目二:
思路1:时间复杂度为O(N*logN)
我们求最长子数组(最短子数组) 这种问题的时候,因为是关于子数组而不是子序列,所以每次可以求 以 index索引位置 为底的(或者开头) 最长子数组的值,这种方式不会丢掉任何一个解,最后做个比较就可以。
这里的思路我们这么来想,求累加和小于等于aim的,比如我们处理到位置30,从位置0到位置30的累加和为100(sum[0..30]=100,现在想求以位置30结尾的,累加和小于等于10的最长子数组。再假设 从 位置0 开始累加到位置8的之后,累加和第一次大于等于90(s[0..8]>=90),那么可以知道以位置30结尾的相加和小于等于10的最长子数组就是arr[9..30].
用一个通用值表示就是,如果从0位置到j位置的累加和为sum[0..j],此时相求以j位置结尾的相加和小于等于k的最长子数组长度,那么只要知道大于等于sum[0..j]-k这个值的累加和最早出现在j之前的什么位置即可,假设这个位置是i位置,那么arr[i+1..j]就是以j结尾的相加和小于等于k的最长子数组。
为了很方便找出大于等于某一个值的累加和最早出现的位置,需要生成一个辅助数组helpArr,含义是每一个元素代表以当前位置i为底部的 子数组中和的最大值
1 首先我们需要记录从-1开始,以每个位置为底的累加和。以[1,2,-1,5,-2]为例,生成的sumArr=[0,1,3,2,7,5]. sumArr中的第一个数0表示 以 位置-1打底的累加和为0
2 生成辅助数组helpArr,也就是表示左侧最大值数组,helpArr=[0,1,3,3,7,7];,为什么原来sumArr数组中的2和5变成3和7呢?因为我们只关心从0开始,以某个位置打底的子数组中大于或者等于一个值的累加和最早出现的位置。比如我们要找的值是m(也就是sum[0..j]-k),比如m等于3,从0开始以位置2打底的数组中,位置1的累加和就大于等于3了,后面的值2就不用看了。所以我们可以8把2变为3,保留的是更大的,出现更早的累加和。(这么变化之后,helpArr数组就会是从小到大的排列顺序,可以使用二分查找了)。
3 helpArr是sunArr每个位置上的左侧最大值数组,所以是有序的,可以通过二分找到第一次大于等于某个值的位置。
以题目中的例子来说明:
arr = [3,-2,-4,0,6], k=-2
1 求出sumArr = [0,3,1,-3,-3,3],进而求出helpArr = [0,3,3,3,3,3]
2 开始遍历,j=0 sum[0..0]=3,此时helpArr中二分查找大于等于3-k = 3-(-2) = 5 这个值第一次数显的位置,没有。所以以0位置结尾的所有子数组累加和没有小于等于k的
3 j=1 sum[0..1]=1 1-k=3 ,helpArr中查找值等于3的位置,查到了,位置是1, arr对应位置是0,所以arr[1..1] 是满足 小于等与k的最长数组
4 j=2 sum[0..2]=-3,helpArr中查找到大于等于-1这个值第一次出现的位置,在helpArr中的位置是0,arr中对应的位置是-1,表示一个数都不累加的情况,所以arr[0..2]是满足条件的最长数组
5 j=3, sum[0..3] = -3,helpArr中查找大于等于-1这个值第一次出现的位置,在helpArr中的位置是0,对应arr中位置是-1,所以一个数都不累加的情况,所以arr[0..3]是满足条件的最长数组
6 j=4,sum[0..4]=3,helpArr中查找大于等于5这个值第一次出现的位置.没有,所以以位置4打底的所有子数组累加后没有小于等于k的
代码:
int getLessIndex(vector<int>&arr,int num) { int low=0; int high = arr.size()-1; int mid = 0; int res = -1; while (low<=high) { mid = (low+high)/2; if(arr[mid]>=num){ res = mid; high = mid-1; } else{ low = mid+1; } } return res; } int maxLength(vector<int>&arr,int k) { // vector<int>h(arr.size()+1); int sum = 0; h[0]=sum;//-1位置的最大累加和为0 for (int i=0; i!=arr.size(); i++) { sum += arr[i]; h[i+1] = max(sum,h[i]); } sum = 0; int res = 0; int pre = 0; int len = 0; for (int i=0; i!=arr.size(); i++) { sum += arr[i]; //找到0-i 数组位置中,最早大于等于sum-k的位置 pre = getLessIndex(h, sum-k); len = pre==-1?0:i-pre+1; res = max(res,len); } return res; }
思路2:时间复杂度为O(N)
首先我们先实现两个辅助数组sums和ends
sums数组的含义:以位置i开头的子数组的最小和
ends数组的含义:以位置i开头的子数组的最小和的右边界
举例说明:
数组arr为 [1,3,-1,-5,4]
sums = [-2,-3,-6,-5,4]
ends = [3,3,3,3,4]
如何求这两个数组呢?我们可以运用dp的思想,从数组的后面向前求解。
比如求解以 i位置开头的最小和,我们要求( i,i),(i,i+1),(i,i+1...) 的所有和中最小的,因为是从后向前求 i+1..开头的已经求出来了,只需要判断i+1..的最小和
是否是负数,是负数,i位置开头的有利可图,把那部分拿过来,如果是正数,i 加上后面的部分只能使结果更大,所以只保留自己。
也就是如下代码:
if (sums[i + 1] < 0) {//情况1 sums[i] = arr[i] + sums[i + 1]; ends[i] = ends[i + 1]; } else { //情况2 sums[i] = arr[i]; ends[i] = i; }
有了这两个辅助数组,接下来我们就开始求解小于等于k的最长数组了
我们既然知道了数组中哪一块 和最小,我们从头开始遍历数组,计算以每个位置开头的 小于等于k的最长数组,遍历完位置1,求出一个值,在遍历位置2,又求出一个值,。。 最后比较最大的。
代码可以如下实现:
int maxLengthNormal(vector<int>&arr, int aim) { if (arr.size() == 0) { return 0; } vector<int>sums(arr.size()); vector<int>ends(arr.size()); //sums[i]表示以位置i为开头的子数组最小和 sums[arr.size() - 1] = arr[arr.size() - 1]; //ends[i]表示以位置i为开头的最小和子数组的最后一个元素位置 ends[arr.size() - 1] = (int)arr.size() - 1; //从倒数第二个位置开始计算sums和ends,借助的思路是 dp //因为计算sums[i]的时候我们已经求出了sums[i-1],那么sums[i]的计算会出现2种情况 // 1 sums[i-1]是否为负数,是的话,sums[i]有利可图,可以变得更小,那就把sum[i-1]拿过来,ends[i]就是ends[i+1] // 2 sums[i-1]是正数,sums[i]无利可图,那就只包含自己。 for (int i = (int)arr.size() - 2; i >= 0; i--) { if (sums[i + 1] < 0) {//情况1 sums[i] = arr[i] + sums[i + 1]; ends[i] = ends[i + 1]; } else { //情况2 sums[i] = arr[i]; ends[i] = i; } } int R = 0;//右边界 int sum = 0; int len = 0; for (int start = 0; start < arr.size(); start++) { //如果 while (R < arr.size() && sum + sums[R] <= aim) { sum += sums[R]; R = ends[R] + 1; } printf("以%d开头的子数组最小和长度=%d\n",start,R - start); len = max(len, R - start); //R回退,从start的下一个位置继续开始,最后导致时间复杂度为O(N^2) R=start+1; sum=0; } return len; }
这种方法必然是不行的,有没有一种优化方法,让R不回退。
这种让R不回退的思路就是这个题目的精华方法
比如我们从位置0开始统计子数组最长,然后根据sums和ends数组我们扩到了区间T,然后从区间T+1开始,累加和就大于k了,没法继续扩了,所以我们就可以得出
从位置0开始的子数组最长的值。下面我们开始统计位置1. 从位置1开始扩,sum首先减去arr[0],表示去除arr[0]之后 是否可以把区间T+1扩进来
如果扩不进来,那说明 从位置1开始的最长子数组和 必定不是我们要的答案
因为不管 从位置1开始扩 是 没有到达区间T,还是正好到达区间T,都会小于我们之前从位置0开始的最长子数组,我们只关心更长的。 所以以位置1开头的最长子数组的和 如果不能从T+1区间继续扩,那么我们不需要统计 。直接从位置2开始进行下一轮的统计即可。
如图所示:
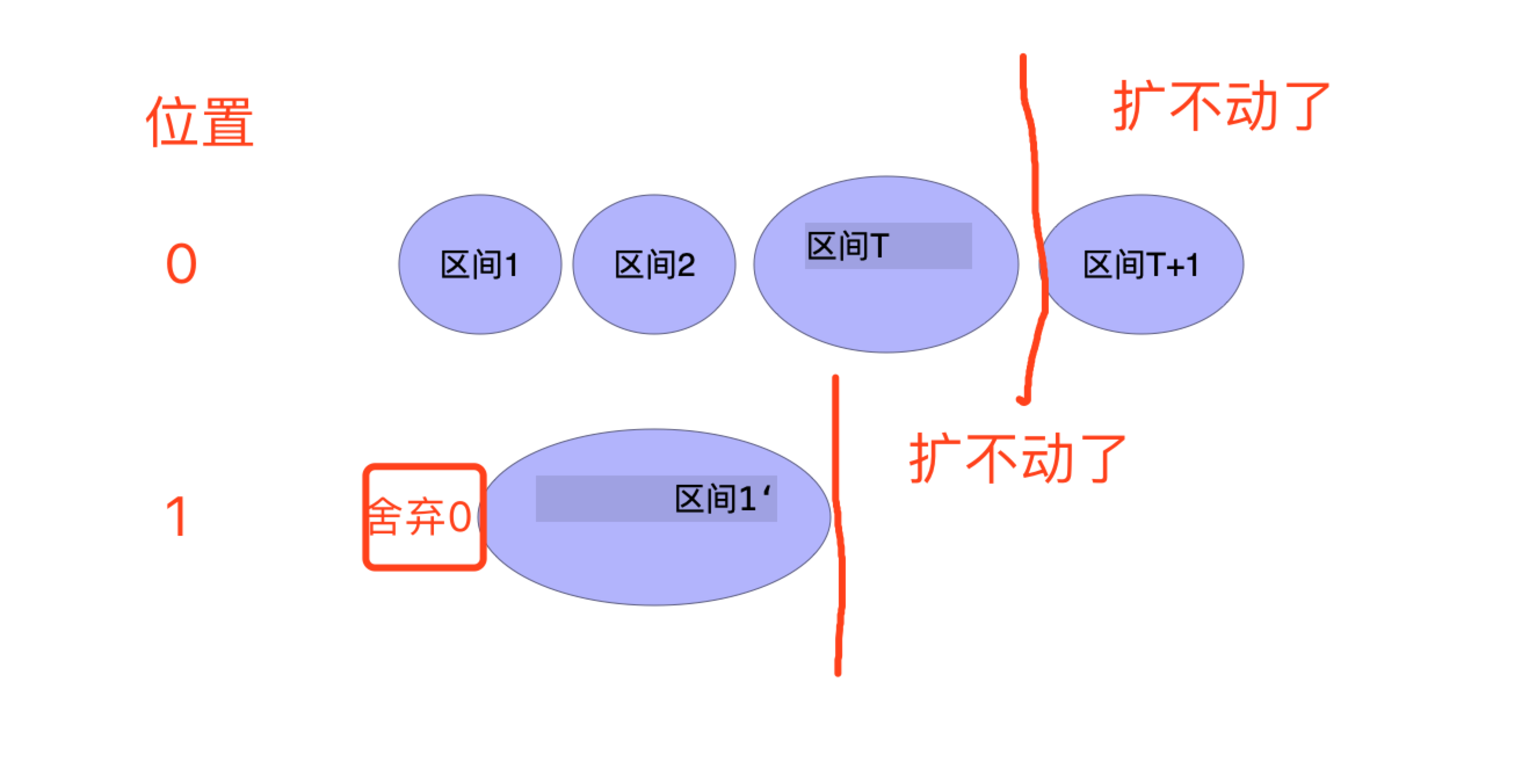
下面以数组[-7,1,6,7,200,-6],aim=7来进行流程说明。
首先统计出sums和ends
sums=[-7,1,6,7,194,-6]
ends=[0,1,2,3,5,5]
1 start=0 -7 <=7 继续从位置1开始扩,-7+1 <=7 继续往位置2扩 ,-7+1+6<=7 ,继续往位置3开始扩,-7+1+6+7<=7,继续往位置4扩,此时 -7+1+6+7+194>7,停
此时 R=4,len=4, maxLength=4
2 start=1 sum=1+6+7=14 ,14+194>7,仍然扩不动,此时R=4,len=3(实际从位置1开始的最长子数组并不为3,其实为2,但是我们的设计就是R不回退,对于小于当前最长的值,我们不关心,不影响最终结果) ,maxLength=4
3 start=2 sum = 13,13+194>7 ,仍然扩不动,此时R=4,len=2,maxLength=4
4 start=3 sum=7,7+194>7 ,扩不动,此时R=4,len=1,maxLength=4
5 start=4 sum=194 >7 ,扩不动,此时R=4,len=0,maxLength=4
6 start=5,sum=-6<=7, 符合条件,此时R=5,len=1,maxLength=4
7 start=6 ,数组遍历完毕,maxLength=4
代码:
int maxLengthAwesome(vector<int>&arr, int aim) { if (arr.size() == 0) { return 0; } vector<int>sums(arr.size()); vector<int>ends(arr.size()); //sums[i]表示以位置i为开头的子数组最小和 sums[arr.size() - 1] = arr[arr.size() - 1]; //ends[i]表示以位置i为开头的最小和子数组的最后一个元素位置 ends[arr.size() - 1] = (int)arr.size() - 1; //从倒数第二个位置开始计算sums和ends,借助的思路是 dp //因为计算sums[i]的时候我们已经求出了sums[i-1],那么sums[i]的计算会出现2种情况 // 1 sums[i-1]是否为负数,是的话,sums[i]有利可图,可以变得更小,那就把sum[i-1]拿过来,ends[i]就是ends[i+1] // 2 sums[i-1]是正数,sums[i]无利可图,那就只包含自己。 for (int i = (int)arr.size() - 2; i >= 0; i--) { if (sums[i + 1] < 0) {//情况1 sums[i] = arr[i] + sums[i + 1]; ends[i] = ends[i + 1]; } else { //情况2 sums[i] = arr[i]; ends[i] = i; } } //下面是整个代码的精华部分 int R = 0;//右边界,不回退,扩到当前sum<=aim的最后位置的下一个位置 int sum = 0; int len = 0; //-7,1,6,7,200,-6 for (int start = 0; start < arr.size(); start++) { //如果 while (R < arr.size() && sum + sums[R] <= aim) { sum += sums[R]; R = ends[R] + 1; } if(R>start){ //常规情况,每次start向右移动一个位置,sum减去之前的位置,然后看看是否可以向前h扩 sum -= arr[start]; } else {//扣边界情况,比如当前R和start在一个位置sum保持不变 sum -= 0; } printf("Best 以%d开头的子数组最小和长度=%d\n",start,R - start); len = max(len, R - start);// R-1 - start +1 表示start到R-1之间的长度 if(R>=start+1){//常规情况,R只要在start右边,那么下次只需要 移动start,R代表不能扩的左边界位置 R = R;//保持不动 } else {//扣边界情况,R和start相等的时候(R没扩动),R要移动到start的下一个位置,因为下一个循环start会加一,要让他们重合 R = start+1; } } return len; }
让我们来比较下
maxLengthNormal
maxLengthAwesome
两个方法的打印结果
vector<int>vec={-7,1,6,7,200,-6}; maxLengthNormal(vec,7); maxLengthAwesome(vec,7);
打印结果:
以0开头的子数组最小和长度=4
以1开头的子数组最小和长度=2
以2开头的子数组最小和长度=1
以3开头的子数组最小和长度=1
以4开头的子数组最小和长度=0
以5开头的子数组最小和长度=1
Best 以0开头的子数组最小和长度=4
Best 以1开头的子数组最小和长度=3
Best 以2开头的子数组最小和长度=2
Best 以3开头的子数组最小和长度=1
Best 以4开头的子数组最小和长度=0
Best 以5开头的子数组最小和长度=1
通过打印结果看出:
maxLengthNormal会正确统计出以每个位置开头的 小于等于k的 最长子数组的长度
maxLengthAwesome有的位置统计是不正确的,因为R不回退,但是这并没有影响正确结果,因为它只关心 更大值,小于当前最大值的长度无关紧要
题目三 环形单链表的约瑟夫问题
据说著名犹太历史学家Josephus有过以下故事:在罗马人占领乔塔帕特后, 39个犹太人与Josephus及他的朋友躲到一个洞中,39个犹太人决定宁愿死也 不要被敌人抓到,于是决定了一个自杀方式,41个人排成一个圆圈,由第1个 人开始报数,报数到3的人就自杀,然后再由下一个人重新报1,报数到3的人 再自杀,这样依次下去,直到剩下最后一个人时,那个人可以自由选择自己的 命运。这就是著名的约瑟夫问题。现在请用单向环形链表描述该结构并呈现整 个自杀过程。
输入:一个环形单向链表的头节点head和报数的值m。 返回:最后生存下来的节点,且这个节点自己组成环形单向链表,其他节点都 删掉。
进阶: 如果链表节点数为N,想在时间复杂度为O(N)时完成原问题的要求,该怎么实现?
常规思路:
就是根据题意,在单链表中 每数到m的时候,删除一个节点,然后连接 被删除节点的前后节点,直到删除的还剩一个,算法复杂度为O(m*n)
进阶思路:
比如节点数为1~n,等删除其中一个的时候,剩余的节点会重新编号为 1~n-1,然后重复过程,直到最后删除的剩下一个 ,它的编号就为1,最后剩下的这个节点就是我们要找的节点,如果我们找到某个公式,找出这个节点 在 节点数为1~n的时候对应的编号,就是我们要找的答案
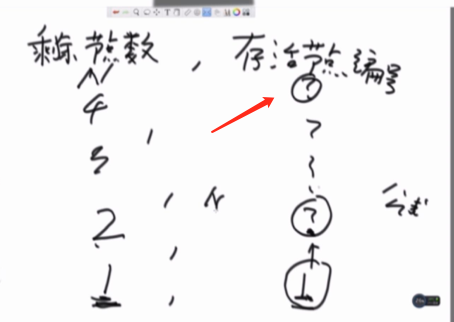
首先我们找出第一个关系公式,如何 在当前链表长度为i的链表中找出要杀死的那个节点
比如现在有3个人,报数到5的人杀死,如图:

通过图可以看出,报数为5的时候,杀死的那个人是编号为2的人。我们就需要找到这样的一个公式,通过报数就可以求出当前长度的链表中对应的人的编号
首先我们来看下图:

公式为 Y=X%i。
而我们报数和编号的坐标图为:

和上图对比就是 x坐标向右移动1个单位,y坐标向上移动一个单位
根据初中数学学过的 左加右减,上加下减 ,可以得出公式为
Y(编号) = (X(报数-1)%i)+1 ,i 为 总人数。
当X=m,Y = (m-1)% i +1
比如m=5的时候 Y=(5-1)% 3 +1 =2
再次,让我们找出第二个公式,就是链表在杀死一个人之后,某人在新链表中的新编号 和 杀死人之前的旧链表中的旧编号 之间的关系
比如 链表长度为i,用户A的编号为k,等杀死一个人的时候,链表长度变为了i-1,用户A的编号变为了m,我们需要找的就是m和k之间的关系,有了这个关系
,我们就可以一层层的推出 链表长度为n的时候,存活用户的编号。
假设长度i的链表,编号为S的人被杀死了,那么i-1的链表编号应该变为,如图所示

编号S在新号没有对应,S 的上一个编号S-1 ,新号就变为 i-1,S+1就变为1 S+2就变为2
举个例子:
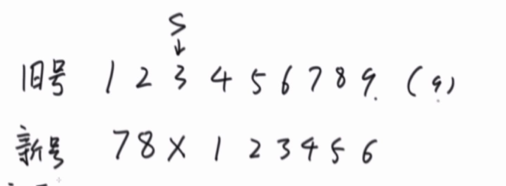
假设S=3,i=9,等S被杀死后,新链表的编号关系就为上图所示。
我们根据关系仍然可以画一个图:(图一)
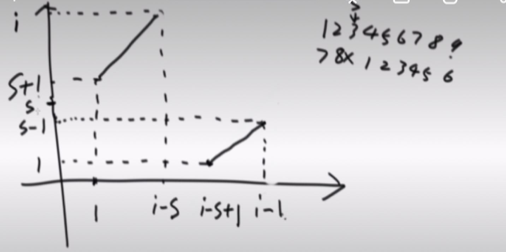
Y轴代表 旧号,X轴代表 新号
旧号为1
新号= 1 - s + i = i-s+1
我们要通过这个图,来推导出 新号和旧号的关系公式。
之前我们直到下图的公式为 Y = (X-1)% i +1
(图2)

我们来找2幅图之间的关系。
首先我们先把图1的线向后延伸
(图3)
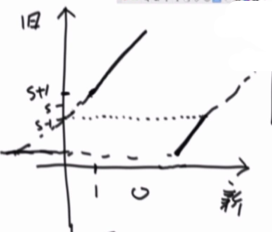
从几个简单的数就可以推出来
图3中:开始的时候 y比x大s
图2中:开始的时候 y=x
二个图的斜率是一样的,只要图2 x 向左平移s(这样整体的x就比y小s了),就可以得到 图3。
根据 左加右减,得到公式:
Y = (X-1+S)% i +1 (1)
Y:旧编号
X:新编号
其中S为旧链表应该删除的 编号
我们之前已经求出链表长度为i,求S的公式了
S=(m-1)%i+1 (2)
把(2) 代入 (1),得到:
Y = (X-1 + (m-1)%i+1 )%i + 1
化简:
Y = (X+(m-1)%i)%i+1
=>
Y= (X+m-1)%i+1
如何推出的呢
比如 U = (a+k%i)%i
假设 k = c*i+T,那么
Y = (a+T)%i
而 (a+k)%i 也等于(a+T)%i
所以可以推出
(X+(m-1)%i)%i+1 == (X+m-1)%i+1
最终公式就为:
旧编号 =( 新编号+m-1)%i+1
假设链表开始的长度为3,数到1 杀人,求最终幸存者的编号。
当 i =1 ,编号 = 1
当i=2 ,编号= (1+ 1 -1 )%2 +1 = 2
当i=3 ,编号 = (2+1-1)%3+1=3
所以 最终幸存者的编号为 3
代码:
public class JosephusProblem { public static class Node { public int value; public Node next; public Node(int data) { this.value = data; } } // 常规做法 public static Node josephusKill1(Node head, int m) { if (head == null || head.next == head || m < 1) { return head; } Node last = head; while (last.next != head) { last = last.next; } int count = 0; while (head != last) { if (++count == m) { last.next = head.next; count = 0; } else { last = last.next; } head = last.next; } return head; } //进阶做法 public static Node josephusKill2(Node head, int m) { if (head == null || head.next == head || m < 1) { return head; } Node cur = head.next; int tmp = 1; // tmp -> list size while (cur != head) { tmp++; cur = cur.next; } tmp = getLive(tmp, m); // tmp -> service node position while (--tmp != 0) { head = head.next; } head.next = head; return head; } public static int getLive(int i, int m) { if (i == 1) { return 1; } return (getLive(i - 1, m) + m - 1) % i + 1; } public static void printCircularList(Node head) { if (head == null) { return; } System.out.print("Circular List: " + head.value + " "); Node cur = head.next; while (cur != head) { System.out.print(cur.value + " "); cur = cur.next; } System.out.println("-> " + head.value); } public static void main(String[] args) { Node head1 = new Node(1); head1.next = new Node(2); head1.next.next = new Node(3); head1.next.next.next = new Node(4); head1.next.next.next.next = new Node(5); head1.next.next.next.next.next = head1; printCircularList(head1); head1 = josephusKill1(head1, 3); printCircularList(head1); Node head2 = new Node(1); head2.next = new Node(2); head2.next.next = new Node(3); head2.next.next.next = new Node(4); head2.next.next.next.next = new Node(5); head2.next.next.next.next.next = head2; printCircularList(head2); head2 = josephusKill2(head2, 3); printCircularList(head2); } }
题目四 字符串匹配问题
【题目】 给定字符串str,其中绝对不含有字符'.'和'*'。再给定字符串exp, 其中可以含有'.'或'*','*'字符不能是exp的首字符,并且任意两个 '*'字符不相邻。exp中的'.'代表任何一个字符,exp中的'*'表示'*' 的前一个字符可以有0个或者多个。请写一个函数,判断str是否能被 exp匹配。
【举例】
str="abc",exp="abc",返回true。 str="abc",exp="a.c",exp中单个'.'可以代表任意字符,所以返回 true。 str="abcd",exp=".*"。exp中'*'的前一个字符是'.',所以可表示任 意数量的'.'字符,当exp是"...."时与"abcd"匹配,返回true。 str="",exp="..*"。exp中'*'的前一个字符是'.',可表示任意数量 的'.'字符,但是".*"之前还有一个'.'字符,该字符不受'*'的影响, 所以str起码有一个字符才能被exp匹配。所以返回false。
思路1:暴力递归
先定义合适的递归函数
process(str,exp,i,j)
含义:
str[i..一直到最后] 这个字符串 ,能不能 被exp[j..一直到最后]这个字符串,匹配出来
process(str,exp,0,0)就是最终返回结果
如何在递归过程中判断 str[i..len] 是否能被 exp[j..len]匹配呢?
需要下面几种情况
假设 当前判断到str的i位置和exp的j位置。
情况1 如果j为exp的结束位置,i为str的结束位置,说明已经全部匹配完毕了(过程之前如果有不匹配的,直接返回false),返回true。
如果i不是str的结束位置,那么肯定返回false,因为i后面的元素没有可以匹配的了。
情况2 如果 j 位置的下一个字符 exp[j+1]不为'*'。那么就必须关注str[i] 能否和 exp[j]匹配。如果能匹配,继续下一个字符的比较,也就是process(str,exp,i+1,j+1)。
如果不匹配,直接返回false
情况3 如果当前j位置的下一个字符 为 '*',这种情况比较复杂,又可以分为2种小情况
3.1 如果str[i]和exp[j]不匹配,那就让exp[j,j+1]这部分为“”,就是让exp[j+1]=='*'字符的前一个字符的exp[j]的数量为0,然后接着考察 process(str,exp,i,j+2)的返回值
3.2 如果str[i]和exp[j]匹配。因为exp[j+1]是*,所以可以表示 exp[j]表示的字符有任意个,就是说 exp[j..j+1]的部分如果能匹配str后续很多位置。那么就一一遍历比较,
有一个返回true,就可以直接返回true
代码如下:
bool process(string & str, string& exp, int i, int j) { //终止条件 if(j==exp.length()){ if(i==str.length()){ return true; } else { return false; } } //1 j后面的字符不是* if(j==exp.length()-1 || exp[j+1]!='*'){ //i 到底了,返回false if(i==str.length()){ return false; } if(exp[j]==str[i] || exp[j]=='.'){//当前字符匹配 //开始匹配下一个 return process(str, exp, i+1, j+1); } else {//不匹配,直接返回false return false; } } /* 2 j后面的字符是 * 分两种情况: 情况1:*前面的字符和str对应的字符不匹配 str = aaaab exp = b*... 情况2:*前面的字符和str对应的字符匹配 str = aaaab exp = a*... 此时有多种匹配模式 */ //情况2 while (i!=str.length() && (str[i]==exp[j] || exp[j]=='.')) { if(process(str, exp, i, j+2)){//有一种情况匹配了,就返回true return true; } i++; } //情况1 return process(str, exp, i, j+2); //说明:j永远不会指向* }
思路二:动态规划
看思路一中的递归函数,有2个可变参数i,j,所以我们需要画一个二维表,大小为(slen+1)*(elen+1). 如下图所示

表红的地方就是我们要求的。
1 老规矩,还是先找baseCase。在precess中,直观看出 就是第一行
if(j==exp.length()){ if(i==str.length()){ return true; } else { return false; } }
当j为最后一行,i也为最后一行的时候返回true,否则返回false,如图:
可以填出最后一列
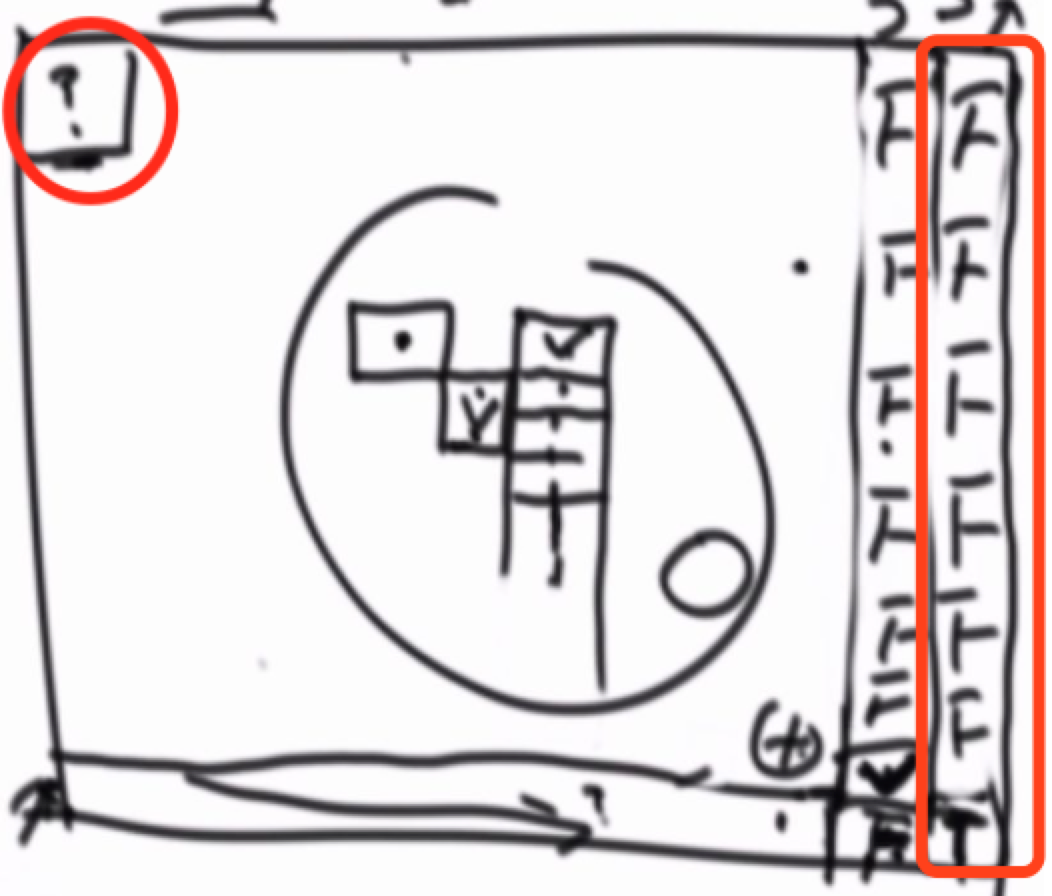
从题意上理解就是,j已经到exp结尾了,此时如果 i没有到str结尾,exp剩下的字符就是'',无法在匹配str剩下的字符了,必然返回false,除非str也到了结尾,也就是说剩下了'',只有此时才能匹配
2 然后我们在找依赖项
从precess递归函数中找,我们找到下面几个地方。


总结来说就是
在递归过程中p(i,j)总是依赖p(i+1,j+1)或者 p(i+k(k>=0),j+2).
假设 dp[i][j]代表p(i,j)的返回值,dp[i][j]就只是依赖pd[i+1][j+1]或者dp[i+k(k>=0)][j+2]的值。如图所示:
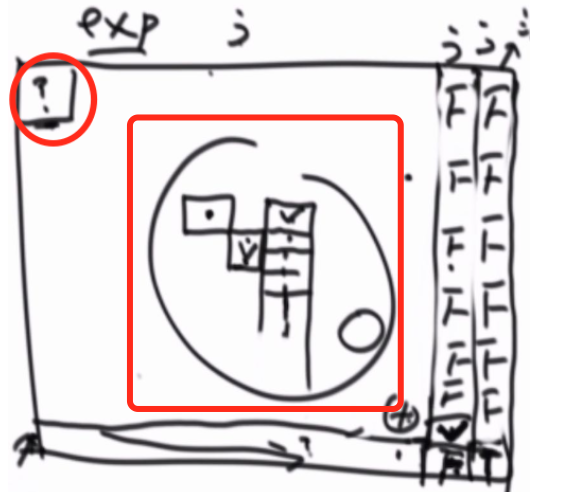
我们求某一个值,至少要知道这个值的下一行的一个数和 隔一列的某几个数,但是从我们目前的baseCase中,很难填满整个表,所以说明我们还需要添加一些数作为
baseCase。这个题和以前 暴力递归推动态规划不同的地方就是,暴力递归的尝试版本有一些baseCase是不那么明确的,这就需要我们返回到题意,根据题意,填写出我们需要的baseCase。
比如这道题,求某一个值,至少要知道这个值的下一行的一个数和 隔一列的某几个数,从这个地方我们猜想,可能需要直到最后一行,和倒数2列,这样才会把整个表填写完毕。
下面回到题意,来填写 倒数第二列。
也就是 dp[0..slen-1][elen-1],从题意上理解就是exp还剩下最后一个字符,即exp[elen-1],而str还剩下1个或多个字符,或者没有字符,也就是只剩下''。
在str只剩下''的时候,exp最后一个字符 不会 匹配,有人会说,exp最后一个是* 能匹配吗?也是不会的,因为从之前的process递归函数中,我们判断从来是判断当前字符的后一个字符是不是*,没有判断当前字符是否为*的逻辑,*的逻辑只会跟着前面的字符来做逻辑处理,没有单独处理 一个*的时候。举一个极端例子,比如开始的时候str='',exp=*,这样显然是不匹配的,因为*只会跟在字符后面。
在str只剩下一个字符的时候,也就是 str[slen-1],如果和exp[elen-1]相等或者exp[elen-1]等于'.'的时候可以匹配
在str剩下二个或者两个以上的字符的时候,不会匹配,因为exp只有一个字符。
这样 我们第二列也可以填写了。如图
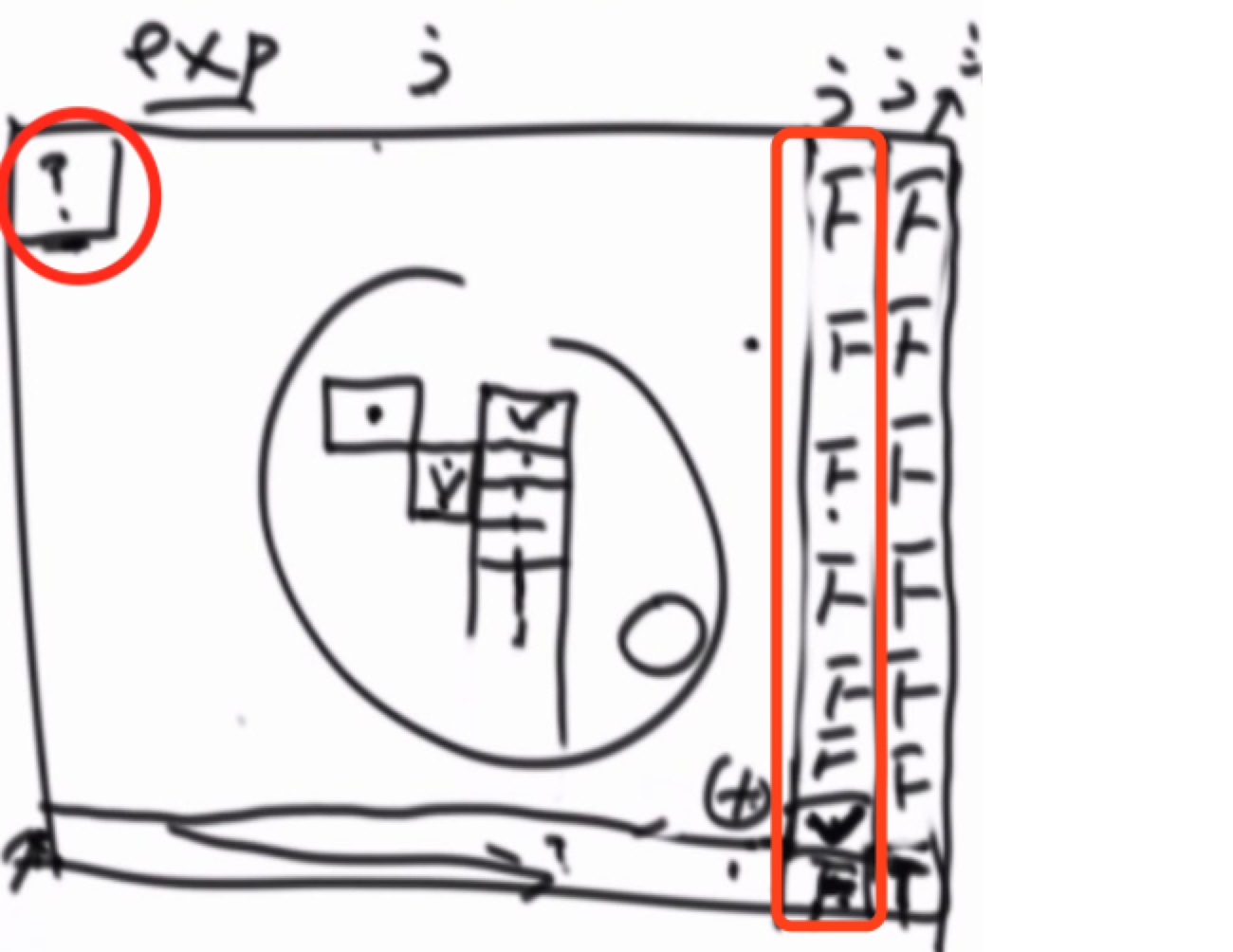
下面我们回到题意,来填写最后一行
题意的意思是 此时str到底了,只剩下''字符,而exp由多个字符。什么情况下会匹配呢,比如下面这种
str abcde'' i =5
exp abcdea*b* j=5
此种情况下是会匹配的,也就是说j从当前字符开始,如果模式为X*X*的模式,才会匹配。
也就是说 从右往左计算dp[slen][0..elen-1]的过程中,看exp是不是从右往左重复出现X*,如果是重复出现,那么如果exp[i]='X',exp[i+1]='*',令dp[slen][i]=true,如果exp[i]=* ,exp[i+1]=X,令dp[slen][i]=false.如果不是重复出现,最后一行后面的部分,即dp[slen][0..i],全部都是false。
这样我们就填写完了最后一行.
这种思路的算法复杂度为:
如果str的长度为N,exp的长度为M,因为有枚举str的过程,所以时间复杂度为O(N^2 * M),额外空间复杂度为O(N*M),代码如下:
public static boolean isValid(char[] str, char[] exp) { for (int i = 0; i < str.length; i++) { if (str[i] == '*' || str[i] == '.') { return false; } } for (int i = 0; i < exp.length; i++) { if (exp[i] == '*' && (i == 0 || exp[i - 1] == '*')) { return false; } } return true; } public static boolean isMatchDP(String str, String exp) { if (str == null || exp == null) { return false; } char[] str = str.toCharArray(); char[] exp = exp.toCharArray(); if (!isValid(str, exp)) { return false; } boolean[][] dp = initDPMap(str, exp); //完全按照递归函数的思路,改成动态规划 for (int i = str.length - 1; i > -1; i--) { for (int j = exp.length - 2; j > -1; j--) { if (exp[j + 1] != '*') { dp[i][j] = (str[i] == exp[j] || exp[j] == '.') && dp[i + 1][j + 1]; } else { int i = i; while (i != str.length && (str[i] == exp[j] || exp[j] == '.')) { if (dp[i][j + 2]) { dp[i][j] = true; break; } i++; } if (dp[i][j] != true) { dp[i][j] = dp[i][j + 2]; } } } } return dp[0][0]; } //填写dp基础部分 /* 初始化完毕之后,就可以得到最后2列和最后一行的值 */ public static boolean[][] initDPMap(char[] str, char[] exp) { int slen = str.length; int elen = exp.length; boolean[][] dp = new boolean[slen + 1][elen + 1]; //最后一行最后一列 dp[slen][elen] = true; //最后一行的赋值,看看模式是否是X*X* for (int j = elen - 2; j > -1; j = j - 2) { if (exp[j] != '*' && exp[j + 1] == '*') { dp[slen][j] = true; } else { break; } } //str 和 exp最后一个字符 if (slen > 0 && elen > 0) { if ((exp[elen - 1] == '.' || str[slen - 1] == exp[elen - 1])) { dp[slen - 1][elen - 1] = true; } } return dp; }



 浙公网安备 33010602011771号
浙公网安备 33010602011771号