牛客周赛 Round 45 F 小橙的圈圈

牛客周赛 Round 45 F 小橙的圈圈

https://ac.nowcoder.com/acm/contest/84244/F

解题思路：

需要观察，一个三元环的构成：

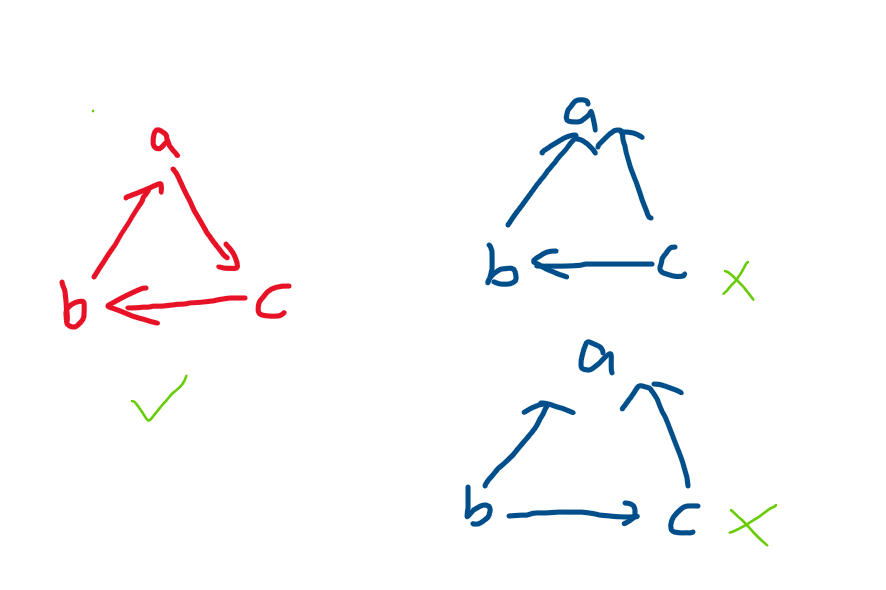
我们想枚举三元环，发现需要 \(O(n^3)\) 的复杂度，但是考虑计数题，我们要想到正难则反，我们考虑求不是三元环的数量，我们发现一个很强的性质就是，对于所有不是三元环的数量，比如满足，三元组中某个点，被剩余两个点指向了。

故我们可以考虑组合数学，枚举那个被指向的点，即记录每个点的入度，我们只要从指向它的所有点中选任意 \(2\) 个，必然构成一个不合法的三元组。

所以最后答案就为：\(\binom{n}{3}-\sum_i^n\binom{in_i}{2}\)

Code

#include <bits/stdc++.h>
typedef long long LL;

const int mod = 1e9 + 7, N = 5010;
int n, seed;
int rnd() {
    int ret = seed;
    seed = (seed * 7LL + 13) % mod;
    return ret % 2;
}

int in[N];

int main() {
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);
    
    std::cin >> n >> seed;
    
    
    LL ans = 1LL * n * (n - 1) * (n - 2) / 6;
    
    for (int i = 1; i <= n; i++) {
        for (int j = i + 1; j <= n; j++) {
            if (rnd() == 0) {
                in[j]++;
            } else {
                in[i]++;
            }
        }
    }
    
    for (int i = 1; i <= n; i++) {
        ans -= 1LL * in[i] * (in[i] - 1) / 2;
    }
    
    std::cout << ans << '\n';
    
    return 0;
}