Codeforces Round 903 (Div. 3)
A. Don't Try to Count
解题思路
我们发现当 \(x.size() < s.size()\) 的时候,我们必须要让 \(x+=x\),当 \(x.size() \ge s.size()\) 的时候,我们只要此时判一下 \(x\) 中是否存在子串 \(s\),存在则马上输出答案,否则只要再执行一次 \(x+=x\)
如果此时还未有解,那么必然是 \(-1\)。(当然,长度很小你直接暴力枚举,一直加也不会加很多次)。
Code
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
void solve() {
int n, m;
cin >> n >> m;
string s, x;
cin >> x >> s;
int ans = 0;
while (x.size() < m) {
x += x;
ans++;
}
if (x.find(s) != -1) {
cout << ans << "\n";
return ;
}
x += x;
if (x.find(s) != -1) {
cout << ans + 1 << "\n";
return ;
}
cout << -1 << "\n";
}
int main() {
cin.tie(nullptr)->sync_with_stdio(false);
int t;
cin >> t;
while (t--) {
solve();
}
return 0;
}
B. Three Threadlets
解题思路
我们可以用一个数组存一下,我们目前分出了哪些数,那么我们发现我们每次必然会把数组里面所有 \(>\) 数组最小值的元素切开。
由于最多执行 \(3\) 次,也是直接暴力模拟即可。
Code
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
void solve() {
int a, b, c;
cin >> a >> b >> c;
if (a == b && b == c) {
cout << "YES\n";
return ;
}
vector<int> cur = {a, b, c};
int cnt = 0;
while (cnt < 3) {
int minv = *min_element(cur.begin(), cur.end());
cnt++;
for (int i = 0; i < cur.size(); i++) {
if (cur[i] > minv) {
cur.push_back(cur[i] - minv);
cur[i] = minv;
break;
}
}
}
for (int i = 0; i < cur.size() - 1; i++) {
if (cur[i] != cur[i + 1]) {
cout << "NO\n";
return ;
}
}
cout << "YES\n";
}
int main() {
cin.tie(nullptr)->sync_with_stdio(false);
int t;
cin >> t;
while (t--) {
solve();
}
return 0;
}
C. Perfect Square
解题思路
我们只要看哪些点必须要相同即可,如图所示:
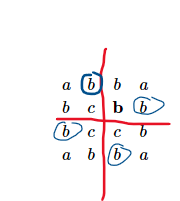
由于 \(n\) 保证是偶数,那么矩阵必然会被划分为 \(4\) 个块,那么显然每个块都和其余块有对称点,我们只要把这些对称点全变成一样即可。
我们发现每次都是 \(4\) 个点为一组,例如图上所标的,由于我们操作只能增加,所以我们只能把这 \(4\) 个点全加到 \(4\) 个字符中最大的那个。
Code
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 1010;
char s[N][N];
void solve() {
int n;
cin >> n;
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) {
cin >> s[i][j];
}
}
int ans = 0;
for (int i = 1; i <= n / 2; i++) {
for (int j = 1; j <= n / 2; j++) {
vector<char> cur = {s[i][j], s[n - j + 1][i], s[j][n - i + 1], s[n - i + 1][n - j + 1]};
char mx = *max_element(cur.begin(), cur.end());
for (auto v : cur){
ans += mx - v;
}
}
}
cout << ans << "\n";
}
int main() {
cin.tie(nullptr)->sync_with_stdio(false);
int t;
cin >> t;
while (t--) {
solve();
}
return 0;
}
D. Divide and Equalize
解题思路
比较思维的一个题,我们直接入手非常困难,我们不可能去模拟这变换的过程。
我们需要找寻突破口,对于这种模拟很复杂的题,变化情况很多的题,我们可以尝试寻找其中的不变量。
那么什么是不变的呢?我们发现对于一次操作:
- \(a_i=\frac{a_i}{x}\),\(a_j=a_j\times x\)
本质上,我们发现他只是发生了因子之间的转移,相当于我把 \(a_i\) 的一个因子除去,然后乘到 \(a_j\) 上。
那么我们就突然发现其中的不变量是什么了,我们发现本质是在进行因子的转移,那么意味着整个数组的质因子个数一定不会变化。
那么我们假设数组中有一个质因子 \(p\) 出现了 \(s\) 次,我们最终要把所有数弄成一样,是不是意味着,此时我数组每一个数的质因子次幂必须完全一样。
相当于我们必须把这 \(s\) 个质因子,分成 \(n\) 组,每组的个数都得一样。
由于操作本质实在进行质因子的转移,那么我们是可以任意分配质因子的,所以我们得出了 YES 的充要条件:
对于数组中所有的不同质因子 \(p\),其出现次数为 \(s\),都满足 \(s\%n=0\)。
Code
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
void solve() {
int n;
cin >> n;
vector<int> a(n);
map<int, int> mp;
for (int i = 0; i < n; i++) {
cin >> a[i];
for (int j = 2; j <= a[i] / j; j++) {
if (a[i] % j == 0) {
int p = 0;
while (a[i] % j == 0) p++, a[i] /= j;
mp[j] += p;
}
}
if (a[i] > 1) mp[a[i]]++;
}
for (auto [x, y] : mp) {
if (y % n) {
cout << "NO\n";
return ;
}
}
cout << "YES\n";
}
int main() {
cin.tie(nullptr)->sync_with_stdio(false);
int t;
cin >> t;
while (t--) {
solve();
}
return 0;
}
E. Block Sequence
解题思路
如果对 DP 比较敏感的,很容易想到用 DP 做。
对于此类子序列选取问题,一般都可以尝试用 DP。
我们可以倒过来 DP,我们设 \(dp[i]\) 表示把 \(i\backsim n\) 变成合法的需要删几个数,转移就非常显然:
- 若选择删除第 \(i\) 个数:\(dp[i] = dp[i + 1] + 1\)。
- 若保留第 \(i\) 个数,说明其后面 \(a_i\) 个数都得保留:\(dp[i] = \min(dp[i], dp[i + a[i] + 1])\)。
Code
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
void solve() {
int n;
cin >> n;
vector<int> a(n + 1);
for (int i = 1; i <= n; i++) {
cin >> a[i];
}
vector<int> dp(n + 2, 1e9);
dp[n + 1] = 0;
for (int i = n; i >= 1; i--) {
dp[i] = dp[i + 1] + 1; // 删了
//不删
if (i + a[i] <= n) {
dp[i] = min(dp[i], dp[i + a[i] + 1]);
}
}
cout << dp[1] << "\n";
}
int main() {
cin.tie(nullptr)->sync_with_stdio(false);
int t;
cin >> t;
while (t--) {
solve();
}
return 0;
}
F. Minimum Maximum Distance
解题思路
比较一眼的树形换根 DP 题,可能还有其它简单的做法。
问题可以转化为,对于所有点 \(i\),都求出当以 \(i\) 为根节点的时候,点 \(i\) 到所有被标记点的最大距离。
换根 DP 跑一下即可。
Code
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
void solve() {
int n, k;
cin >> n >> k;
vector<int> a(n + 1, 0);
for (int i = 0; i < k; i++) {
int x;
cin >> x;
a[x] = 1;
}
vector<vector<int>> g(n + 1);
for (int i = 1; i < n; i++) {
int u, v;
cin >> u >> v;
g[u].push_back(v);
g[v].push_back(u);
}
vector<int> d1(n + 1, -1e9), d2(n + 1, -1e9), up(n + 1, -1e9), pre(n + 1);
function<void(int, int)> dfs1 = [&](int u, int fa) {
if (a[u]) d1[u] = d2[u] = 0;
for (auto v : g[u]) {
if (v == fa) continue;
dfs1(v, u);
if (d1[u] < d1[v] + 1) d2[u] = d1[u], d1[u] = d1[v] + 1, pre[u] = v;
else if (d2[u] < d1[v] + 1) d2[u] = d1[v] + 1;
}
};
function<void(int, int)> dfs2 = [&](int u, int fa) {
for (auto v : g[u]) {
if (v == fa) continue;
if (pre[u] == v) up[v] = max(up[u], d2[u]) + 1;
else up[v] = max(d1[u], up[u]) + 1;
dfs2(v, u);
}
};
dfs1(1, 0);
if (a[1]) up[1] = 0;
dfs2(1, 0);
int ans = 1e9;
for (int i = 1; i <= n; i++) {
ans = min(ans, max(up[i], d1[i]));
}
cout << ans << "\n";
}
int main() {
cin.tie(nullptr)->sync_with_stdio(false);
int t;
cin >> t;
while (t--) {
solve();
}
return 0;
}
G. Anya and the Mysterious String
解题思路
比较明显的线段树题,我们需要维护两种操作:
- 区间加,这个用懒标记搞搞就行。
- 要判断一个区间是否是不存在长度 \(\ge 2\) 的回文串,其等价于判断,是否区间中不存在形如
aa,aba的子串,即我们只要维护相邻两个字符是否相等,以及相邻三个字符是否构成回文串即可。
这个用线段树也很容易维护,只要维护每个区间开头前 \(2\) 个字符,和末尾后 \(2\) 个字符即可。
Code
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 2e5 + 10;
struct Tag {
int tag = 0;
void apply(Tag t) {
tag = (tag + t.tag) % 26;
}
};
struct Info {
int ok = 1, sl[2] = {-1, -1}, sr[2] = {-1, -1}; //开头两个,末尾两个
void apply(Tag t) {
for (int i = 0; i < 2; i++) {
if (sl[i] != -1) sl[i] = (sl[i] + t.tag) % 26;
if (sr[i] != -1) sr[i] = (sr[i] + t.tag) % 26;
}
}
};
Info operator + (const Info &a, const Info &b) {
Info c;
c.ok = a.ok & b.ok;
c.sl[0] = a.sl[0], c.sr[0] = b.sr[0];
if (a.sl[1] != -1) c.sl[1] = a.sl[1];
else c.sl[1] = b.sl[0];
if (b.sr[1] != -1) c.sr[1] = b.sr[1];
else c.sr[1] = a.sr[0];
if (a.sr[0] == b.sl[0]) c.ok = 0;
if (a.sr[1] != -1 && a.sr[1] == b.sl[0]) c.ok = 0;
if (b.sl[1] != -1 && b.sl[1] == a.sr[0]) c.ok = 0;
return c;
}
struct Segtree {
Info info[4 * N];
Tag tag[4 * N];
void pull(int u) {
info[u] = info[u << 1] + info[u << 1 | 1];
}
void apply(int u, const Tag &v) {
info[u].apply(v);
tag[u].apply(v);
}
void push(int u) {
apply(u << 1, tag[u]);
apply(u << 1 | 1, tag[u]);
tag[u] = Tag();
}
void build(int u, int l, int r, string &s) {
info[u] = {1, -1, -1, -1, -1};
tag[u] = Tag();
if (l == r) {
info[u].sl[0] = info[u].sr[0] = s[l - 1] - 'a';
return ;
}
int mid = (l + r) >> 1;
build(u << 1, l, mid, s);
build(u << 1 | 1, mid + 1, r, s);
pull(u);
}
void modify(int u, int l, int r, int pl, int pr, const Tag &v) {
if (l >= pl && r <= pr) {
apply(u, v);
return ;
}
int mid = (l + r) >> 1;
push(u);
if (pl <= mid) modify(u << 1, l, mid, pl, pr, v);
if (pr > mid) modify(u << 1 | 1, mid + 1, r, pl, pr, v);
pull(u);
}
Info query(int u, int l, int r, int pl, int pr) {
if (l >= pl && r <= pr) return info[u];
int mid = (l + r) >> 1;
push(u);
if (pr <= mid) return query(u << 1, l, mid, pl, pr);
else if (pl > mid) return query(u << 1 | 1, mid + 1, r, pl, pr);
return query(u << 1, l, mid, pl, pr) + query(u << 1 | 1, mid + 1, r, pl, pr);
}
} seg;
void solve() {
int n, m;
cin >> n >> m;
string s;
cin >> s;
seg.build(1, 1, n, s);
while (m--) {
int op;
cin >> op;
if (op == 1) {
int l, r, x;
cin >> l >> r >> x;
seg.modify(1, 1, n, l, r, {x});
} else {
int l, r;
cin >> l >> r;
auto res = seg.query(1, 1, n, l, r);
if (!res.ok) {
cout << "NO\n";
} else {
cout << "YES\n";
}
}
}
}
int main() {
cin.tie(nullptr)->sync_with_stdio(false);
int t;
cin >> t;
while (t--) {
solve();
}
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号