数据结构和算法分析 引论+算法分析

数学知识复习

级数运算

 

常用的有：

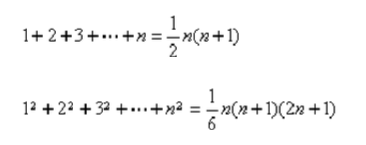
递归算法

递归一般可以条件性的拆分为：

  1. 基准情况：不用递归的那一部分。
  2. 不管推进：递归调用的递归是朝着一个基准情况的方向在推进。

一个简单递归的例子：打印出正整数。基于一个只能打印一个0-9的数字的方法，打印正整数。

如果定义可以打印0-9的数字的方法为g(x)，打印正整数的那么递归的推进表达式可写为为：

f(x) = f(x/10) + g(x%10)

其中g(x)是基准情况。

代码实现为：

  1. package com.zjf;
  2.  
  3. public class Recursive {
  4.  
  5.    public static void main(String[] args) {
  6.       printInt(15623);
  7.    }
  8.  
  9.    public static void printInt(int i)
  10.    {
  11.       if(i > 10)
  12.       {
  13.          printInt(i/10);
  14.       }
  15.       printDigit(i%10);
  16.  
  17.    }
  18.    public static void printDigit(int i )
  19.    {
  20.       if(9>= i && i >= 0)
  21.       {
  22.          System.out.print(i);
  23.       }
  24.       else
  25.       {
  26.          throw new IllegalArgumentException();
  27.       }
  28.    }
  29.  
  30. }

注意，一个递归f(x)，在递归调用f(x)的时候，必须要终止条件。如上面的  if(i > 10)。否则将会陷入死循环。

泛型类型限界

Comparable接口是泛型接口，涉及子类和超类的的情况下，我们一般在需要对比的超类级别上定义对比方法，子类如果覆盖了超类的对比方法，那么这个超类的不同子类之间就不能比较了，代码如下：

  1. package com.zjf;
  2.  
  3.  
  4. public class GenericTest {
  5.  
  6.    public static void main(String[] args) {
  7.       Person zjf = new Person("zjf",30);
  8.       Man zdw = new Man("zdw",27);
  9.       Woman xhj = new Woman("xhj",30);
  10.       System.out.println(zjf.compareTo(zdw));
  11.       System.out.println(zdw.compareTo(xhj));
  12.    }
  13.  
  14. }
  15.  
  16. class Person implements Comparable<Person>{
  17.    private String name;
  18.    private Integer age;
  19.  
  20.    public Person(String name, Integer age) {
  21.       super();
  22.       this.name = name;
  23.       this.age = age;
  24.    }
  25.  
  26.    @Override
  27.    public int compareTo(Person o) {
  28.       return this.age.compareTo(o.age);
  29.    }
  30. }
  31.  
  32. class Man extends Person{
  33.  
  34.    public Man(String name, Integer age) {
  35.       super(name, age);
  36.    }
  37.  
  38. }
  39.  
  40. class Woman extends Person{
  41.  
  42.    public Woman(String name, Integer age) {
  43.       super(name, age);
  44.    }
  45.  
  46. }

运行结果没有问题，由于都是使用Person的对比方法，所以不同子类之间可以对比。

如果此时Woman实现了Comparable< Woman>，那么Woman和Man就不能相互比较了。

我们来实践一下：

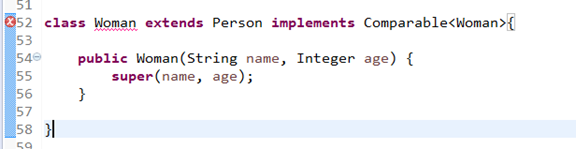
报错了，错误信息是：The interface Comparable cannot be implemented more than once with different arguments:

Comparable<Person> and Comparable<Woman>

因为在java中，Comparable<Person> and Comparable<Woman>和在运行时是一样的，都是Comparable，所以我们不能Woman继承了Person，其实已经实现了Comparable，这里等于再次实现了一次，编译上是通不过的。

那么如果我们不再次实现Comparable，只是试图重写并覆盖超类的compareTo方法呢，如下：

  1. class Woman extends Person {
  2.  
  3.    public Woman(String name, Integer age) {
  4.       super(name, age);
  5.    }
  6.  
  7.    @Override
  8.    public int compareTo(Person o) {
  9.       // TODO Auto-generated method stub
  10.       return super.compareTo(o);
  11.    }
  12. }

这样，即使要重写，参数也只能是Person类型。这里可以做强制转换。但是很不优雅了。

同样，如果使用不加泛型的Comparable，那么所有的参数都是Object类型的，也不是很优雅。

由于Java的泛型不能区分Comparable<Person> and Comparable<Woman>，所以只能如此了。

 

不再纠结这个问题，现在，基于上面的设计，如果我们需要定义一个static的方法，用于实现取一个数组最大值的工具方法。

第一种方法，使用非泛型方法：

  1. public static Comparable findMax(Comparable[] arr)
  2.    {
  3.       return ...;
  4.    }

这种方法，返回类型只能是Comparable的，在使用的时候要强制转换。

下面使用泛型方法重写：

最简单的方法，使用<T extends Comparable>,代码如下：

  1. public static <T extends Comparable> T findMax(T[] arr)
  2.    {
  3.       T max = arr[0];
  4.       for(int i = 1; i<arr.length; i++)
  5.       {
  6.          if(max.compareTo(arr[i]) < 0)
  7.          {
  8.             max = arr[i];
  9.          }
  10.       }
  11.       return max;
  12.    }

 

按照作者的说法，这种写法不太优雅。作者进一步又觉得改造成：

<T extends Comparable<T>>

但是这个不能表示Man，因为Man实现的 是Comparable<Person>,而不是Comparable<Man>.

如下：

 

所以作者又进一步改成了：

<T extends Comparable<? super T>>

这样作者就满足了。。

事实上，我在实验的时候，如通过如下代码试验：

  1. public static void main(String[] args) {
  2.       Person zjf = new Person("zjf",30);
  3.       Man zdw = new Man("zdw",27);
  4.       Woman xhj = new Woman("xhj",30);
  5.       Person[] c = new Person[]{zjf,zdw,xhj};
  6.       findMax(c);
  7.    }

上面的几种写法，编译器都是一样认可的。因为我声明数组的时候是用的Person。对于编译器来说，一个  Person对象满足了 <T extends Comparable>,<T extends Comparable<T>> , <T extends Comparable<? super T>>三种。

思考：什么时候使用泛型方法？

当一组操作针对多种类型参数时使用，比如上面的findMax方法，它要对一组继承自Comparable接口的数据进行处理。特别参数中是对数组和集合进行操作，其实结果返回的是集合中的具体类型

运行时间计算

 

一个简单的例子：

  1. public static long getSum(int n){
  2.       long sum = 0;
  3.       for(int i = 0;i< n;i++)
  4.       {
  5.          sum += n*n*n;
  6.       }
  7.       return n;
  8.    }

时间复杂度在意的是随着N的扩大，极限情况下的复杂度。这里假设第5行的时间复杂度为10，第2行的为1，那么这方法的时间复杂度为10N + 1，我们记为O(N)。

常见的算法时间复杂度由小到大依次为：Ο(1)＜Ο(log2n)＜Ο(n)＜Ο(nlog2n)＜Ο(n2)＜Ο(n3)＜…＜Ο(2n)＜Ο(n!)

最大子序列和问题求解

最大子序列和：求一个数组中所有子序列中和最大的那个和。

如-1，2，5，-6，3。最大子序列是2,5。和是7.

以下所有算法都假设

  • 第一种算法：
  1. public static int getBigSum(int[] arr){
  2.       int sum = arr[0];
  3.       for(int i =0; i< arr.length; i++)
  4.       {
  5.          for(int j = i; j < arr.length; j++)
  6.          {
  7.             int sumTemp = 0;
  8.             for(int x = i; x <=j; x++ )
  9.             {
  10.                sumTemp += arr[x];
  11.             }
  12.             if(sumTemp > sum)
  13.             {
  14.                sum = sumTemp;
  15.             }
  16.          }
  17.       }
  18.       return sum;
  19.    }

我们来看复杂度：

第一层循环次数为N

第二层循环次数为(1到N) = N + (N-1) + (N-2) + …1 = N*(N+1)/2 ≈ N2/2。

第三层循环的次数为：(1到N) + (1到N-1) + (1到N-2) … + (1到1) = N2/2 + (N-1)2/2 + … =(N*(N+1)*(2N+1)/6)/2 = N3/6

最终的算法复杂度是取第三层执行的次数，也就是O(N3)。

  • 第二种算法：
  1. ublic static int getBigSum(int[] arr){
  2.       int sum = arr[0];
  3.       for(int i =0; i< arr.length; i++)
  4.       {
  5.          for(int j = i; j < arr.length; j++)
  6.          {
  7.             int sumTemp = 0;
  8.             for(int x = i; x <=j; x++ )
  9.             {
  10.                sumTemp += arr[x];
  11.             }
  12.             if(sumTemp > sum)
  13.             {
  14.                sum = sumTemp;
  15.             }
  16.          }
  17.       }
  18.       return sum;
  19.    }

 

我们来看复杂度：

第一层循环次数为N

第二层循环次数为(1到N) = N + (N-1) + (N-2) + …1 = N*(N+1)/2 ≈ N2/2。

所以复杂度为O(N2)。

  • 第三种算法：
  1. public static int getBigSum3(int[] arr)
  2.    {
  3.       return getBigSumRec(arr,0,arr.length-1);
  4.    }
  5.  
  6.    /**
  7.     *
  8.     * @param arr 数组
  9.     * @param left 左下标
  10.     * @param right 右下标
  11.     * @return
  12.     */
  13.    public static int getBigSumRec(int[] arr,int left,int right){
  14.       //基准情况
  15.       if(left == right)
  16.       {
  17.          return arr[left];
  18.       }
  19.       //拆分为两半
  20.       int center = (left + right)/2;
  21.       //现在 有两种情况
  22.       //一种是最大值序列不包含中间的center下标的值 那么就是递归左侧getBigSumRec(arr,left,center)或者右侧getBigSumRec(arr,center + 1,right)
  23.       //一种是最大值序列包含中间的center下标的值 肯定不是上面两种情况了，而是：
  24.       //从center向左遍历到left的最大序列值 + center向右表里到right的最大值序列
  25.       //递归计算左侧
  26.       int maxLeftSum = getBigSumRec(arr,left,center);
  27.       //递归计算右侧
  28.       int maxRightSum = getBigSumRec(arr,center + 1,right);
  29.  
  30.       int maxLeftBorderSum = arr[center];
  31.       int leftBorderSum = 0;
  32.       for(int i = center; i >= left; i--)
  33.       {
  34.          leftBorderSum += arr[i];
  35.          if(leftBorderSum > maxLeftBorderSum )
  36.          {
  37.             maxLeftBorderSum = leftBorderSum;
  38.          }
  39.       }
  40.  
  41.       int maxRightBorderSum = arr[center+1];
  42.       int rightBorderSum = 0;
  43.       for(int i = center + 1; i <= right; i++)
  44.       {
  45.          rightBorderSum += arr[i];
  46.          if(rightBorderSum > maxRightBorderSum )
  47.          {
  48.             maxRightBorderSum = rightBorderSum;
  49.          }
  50.       }
  51.       return max3(maxLeftSum,maxRightSum,maxLeftBorderSum + maxRightBorderSum);
  52.    }
  53.    //返回三个数值中的最大值
  54.    private static int max3(int i, int j, int k) {
  55.       int max = i;
  56.       if(j > max)
  57.       {
  58.          max = j;
  59.       }
  60.       if(k > max)
  61.       {
  62.          max = k;
  63.       }
  64.       return max;
  65.    }

因为第一层循环是是折半递归，所以复杂度为logN，第二层循环是两个for循环，复杂度为N。所以整个复杂度为O(NlogN)。

  • 第三种算法：
  1. public static int getBigSum4(int[] arr){
  2.       //最大序列和
  3.       int sum = arr[0];
  4.       //局部序列和
  5.       int sumTemp = 0;
  6.       //解释一下上面的两个初始值的设置
  7.       //因为只是sum对比和赋值 所以初始值不能设置为0 否则如果全是负值 那么结果会是0
  8.       //因为sumTemp的值是根据+计算出来的 所以初始这可以设置为0
  9.  
  10.       for(int i =0; i< arr.length; i++)
  11.       {
  12.          sumTemp += arr[i];
  13.          if(sumTemp > sum )
  14.          {
  15.             sum = sumTemp;
  16.          }
  17.          //如果局部序列和为负值 那么我们就可以舍弃它 重新开始一个局部序列了
  18.          //因为一个和为负值的局部序列和 不管下一个数值是正负 累加后都会小于下一个数值 所以我们直接从下一个数值开始一个新的序列
  19.          if(sumTemp < 0)
  20.          {
  21.             sumTemp = 0;
  22.          }
  23.       }
  24.       return sum;
  25.    }

很明显，时间复杂度为O(N)。

对数复杂度

如果一个算法用常数时间O(1)将问题的大小削减为其一部分,通常为1/2，那么该算法的复杂度就是O(logN)。

最简答的例子就是折半查找（二分查找）：

  1. public static <T extends Comparable<? super T>> int binarySerch(T[] arr, T t) {
  2.       int left = 0;
  3.       int right = arr.length - 1;
  4.       while(left <= right)
  5.       {
  6.          int middle = (left + right)/2;
  7.          if(arr[middle].compareTo(t) > 0)
  8.          {
  9.             right = middle - 1;
  10.          }
  11.          else if(arr[middle].compareTo(t) < 0)
  12.          {
  13.             left = middle + 1;
  14.          }
  15.          else
  16.          {
  17.             return middle;
  18.          }
  19.       }
  20.       return -1;
  21.    }

复杂度为O(logN)。

另外一个例子，幂运算：

  1. public static long pow(long x, int y) {
  2.       long result = 0;
  3.       if (y == 0) {
  4.          return 1;
  5.       }
  6.       if (y == 1) {
  7.          return x;
  8.       }
  9.       // 偶数
  10.       if (y % 2 == 0) {
  11.          long temp = pow(x, y / 2);
  12.          return temp * temp;
  13.          //书上写的是 return power(x*x,y/2)
  14.       }
  15.       // 偶数
  16.       if (y % 2 == 1) {
  17.          long temp = pow(x, y / 2);
  18.          return temp * temp * x;
  19.          //书上写的是 return power(x*x,y/2) * x
  20.       }
  21.       return result;
  22.    }

时间复杂度为O(logN)

如果使用y遍循环，做x*x，那么时间复杂度是O(N)。

 

posted on 2017-07-06 23:08  张小贱1987  阅读(196)  评论(0)  编辑  收藏  举报

导航