构建乘积数组

给定一个数组A[0,1,...,n-1],请构建一个数组B[0,1,...,n-1],其中B中的元素B[i]=A[0]*A[1]*...*A[i-1]*A[i+1]*...*A[n-1]。不能使用除法。

（注意：规定B[0] = A[1] * A[2] * ... * A[n-1]，B[n-1] = A[0] * A[1] * ... * A[n-2];）

题解：

仔细观察会发现题目要求得是：B[i] = A[0]累乘到A[n-1] / A[i]

就是从0累乘到最后然后除去当前对应的A【i】

但是题目不让用除法。

首先想到的思路是双层循环，但是时间复杂度太高了O(N2)不推荐

这里

不妨设定C[i]=A[0]*A[1]*...*A[i-1]，D[i]=A[i+1]*...*A[n-2]*A[n-1]。

C[i]可以用自上而下的顺序计算出来，即C[i]=C[i-1]*A[i-1]。

类似的，D[i]可以用自下而上的顺序计算出来，即D[i]=D[i+1]*A[i+1]。

参考下面的图

红色部分代表第一个循环要求得，绿色代表第二个要求得

 

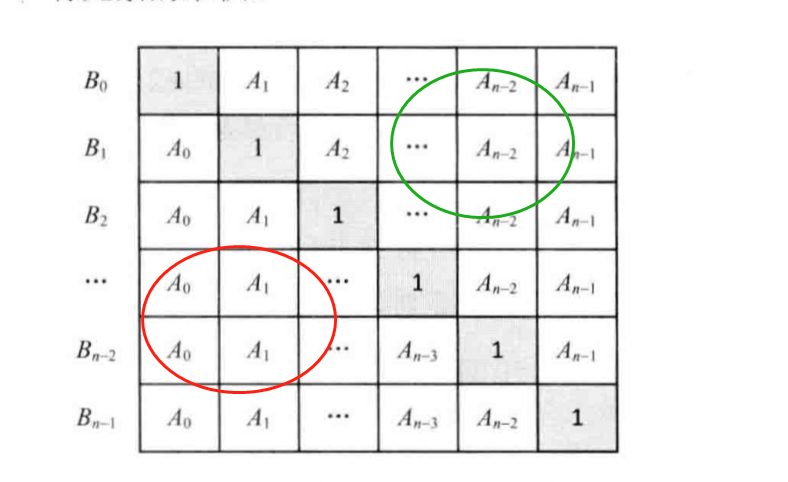
 注意：B[i] = B[i-1]*A[i-1];

#include <iostream>
#include <vector>
using namespace std;
// 画出那个乘积的表格，
// 第一个循环代表前半部分，后一个循环代表后半部分
class Solution {
public:
    vector<int> multiply(const vector<int>& A) {

        int len = A.size();
        if (len <= 0)
            return {};
        vector<int> B(len);
        B[0] = 1;

        // 前半部分
        for(int i = 1; i < len; i++)
        {
            B[i] = B[i-1]*A[i-1];
        }
        // 后半部分
        int temp = 1;  // i = len-2是从倒数第二个开始的
        for(int i = len-2; i>=0; --i)
        {
            temp *= A[i+1];
            B[i] *= temp;
        }
        return B;
    }
};
int main(void)
{
    Solution s;
    vector<int> vec = {1,2,3,4,5};
    vec = s.multiply(vec);
    for(auto it : vec)
            cout << it << " ";
    return 0;
}