数据结构学习--Java删除二叉树节点

想了半天，是真的不好想（手动捂脸）

三种情况需要考虑：

1、该节点是叶子节点，没有子节点

要删除叶节点，只需要改变该节点的父节点的引用值，将指向该节点的引用设置为null就可以了。

 

 

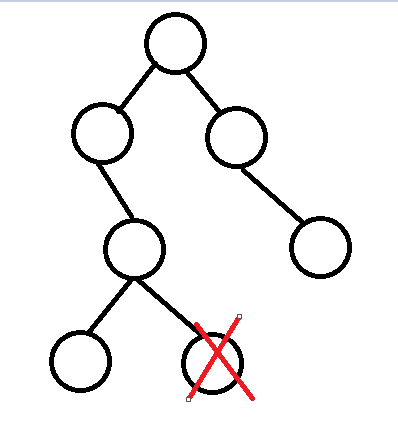
2、该节点有一个子节点

改变父节点的引用，将其直接指向要删除节点的子节点。

 

 

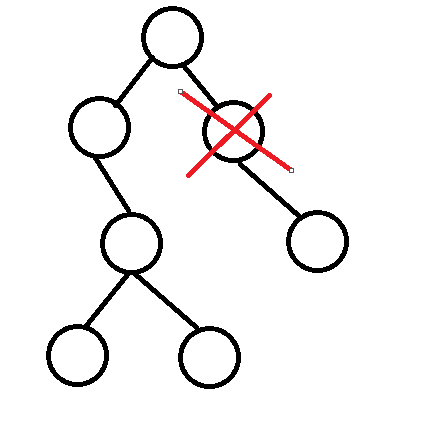
3、该节点有两个子节点

要删除有两个子节点的节点，就需要使用它的中序后继来替代该节点。

 

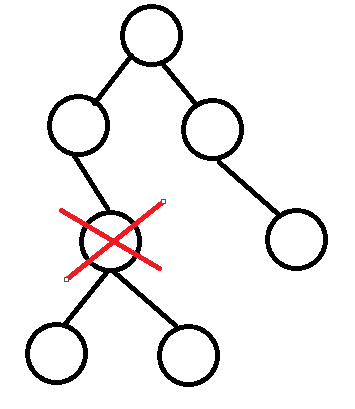
 代码

package com.example.deer;

public class Tree {
    //根节点
    public Node root;

    /**
     * 插入节点
     * @param value
     */
    public void insert(long value,String sValue){
        //封装节点
        Node newNode = new Node(value,sValue);
        //引用当前节点
        Node current = root;
        //引用父节点
        Node parent;
        //如果root为null，也就是第一次插入的时候
        if(root == null){
            root = newNode;
            return;
        }else{
            while (true){
                //父节点指向当前节点
                parent = current;
                //如果当前指向的节点数据比插入的要大，则向左走
                if(current.data > value){
                    current = current.leftChild;
                    if(current == null){
                        parent.leftChild = newNode;
                        return;
                    }
                }else{
                    current = current.rightChild;
                    if(current == null){
                        parent.rightChild = newNode;
                        return;
                    }
                }
            }
        }
    }
    /**
     * 查找节点
     */
    public Node find(long value){
        //引用当前节点，从根节点开始
        Node current = root;
        //循环，只要查找值不等于当前节点的数据项
        while(current.data != value){
            //进行比较，比较查找值和当前节点的大小
            if(current.data > value){
                current = current.leftChild;
            } else {
              current = current.rightChild;
            }
            if(current == null){
                return null;
            }
        }
        return current;
    }

    /**
     * 删除节点
     */
    public boolean delete(long value){
        //引用当前节点，从根节点开始
        Node current = root;
        //应用当前节点的父节点
        Node parent = root;
        //是否为左节点
        boolean isleftChild = true;

        while(current.data != value){
            parent = current;
            //进行比较，比较查找值和当前节点的大小
            if(current.data > value){
                current = current.leftChild;
                isleftChild = true;
            } else {
                current = current.rightChild;
                isleftChild = false;
            }
            if(current == null){
                return false;
            }
        }
        //删除叶子节点，也就是该节点没有子节点
        if(current.leftChild == null && current.rightChild == null){
            if(current == root){
                root = null;
            }else if(isleftChild){//如果它是父节点的左子节点
                parent.leftChild = null;
            }else{
                parent.rightChild = null;
            }
        }else if (current.rightChild == null){
            if(current == root){
                root = current.leftChild;
            }else if(isleftChild){
                parent.leftChild = current.leftChild;
            }else{
                parent.rightChild = current.leftChild;
            }
        }else if (current.leftChild == null){
            if(current == root){
                root = current.rightChild;
            }else if(isleftChild){
                parent.leftChild = current.rightChild;
            }else{
                parent.rightChild = current.rightChild;
            }
        } else {
            Node successor = getSuccessor(current);
            if(current == root){
                root = successor;
            } else if(isleftChild) {
                parent.leftChild = successor;
            }else{
                parent.rightChild = successor;
            }
            successor.leftChild = current.leftChild;
        }
        return true;
    }

    /**
     * 寻找中继节点
     * @param delNode
     * @return
     */
    public Node getSuccessor(Node delNode){
        Node successor = delNode;
        Node successorParent = delNode;
        Node current = delNode.rightChild;
        while(current != null){
            successorParent = successor;
            successor = current;
            current = current.leftChild;
        }
        if(successor != delNode.rightChild){
            //
            successorParent.leftChild = successor.rightChild;
            //将删除的节点的整个右子树挂载到中继节点的右子树上
            successor.rightChild = delNode.rightChild;
        }
        return successor;
    }
    /**
     * 前序遍历
     */
    public void frontOrder(Node localNode){
        if(localNode != null){
            //访问根节点
            System.out.println(localNode.data + "," + localNode.sData);
            //前序遍历左子树
            frontOrder(localNode.leftChild);
            //前序遍历右子树
            frontOrder(localNode.rightChild);
        }
    }

    /**
     * 中序遍历
     */
    public void inOrder(Node localNode){
        if(localNode != null){
            //中序遍历左子树
            inOrder(localNode.leftChild);
            //访问根节点
            System.out.println(localNode.data + "," + localNode.sData);
            //中序遍历右子树
            inOrder(localNode.rightChild);
        }
    }
    /**
     * 后序遍历
     */
    public void afterOrder(Node localNode){
        if(localNode != null){
            //后序遍历左子树
            afterOrder(localNode.leftChild);
            //后序遍历右子树
            afterOrder(localNode.rightChild);
            //访问根节点
            System.out.println(localNode.data + "," + localNode.sData);
        }
    }
}