观摩三叶的读后感
以下是读三叶大佬文章的笔记。
双指针:
【面试高频系列】可逐层递进的经典题,以及如何根据「数据范围」调整使用何种算法
题目:
难度中等
给定一个由若干 0 和 1 组成的数组 A,我们最多可以将 K 个值从 0 变成 1 。
返回仅包含 1 的最长(连续)子数组的长度。
示例 1:
输入:A = [1,1,1,0,0,0,1,1,1,1,0], K = 2
输出:6
解释:
[1,1,1,0,0,1,1,1,1,1,1]
粗体数字从 0 翻转到 1,最长的子数组长度为 6。
示例 2:
输入:A = [0,0,1,1,0,0,1,1,1,0,1,1,0,0,0,1,1,1,1], K = 3
输出:10
解释:
[0,0,1,1,1,1,1,1,1,1,1,1,0,0,0,1,1,1,1]
粗体数字从 0 翻转到 1,最长的子数组长度为 10。
提示:
1 <= A.length <= 200000 <= K <= A.lengthA[i]为0或1
题目是给一个数组,全是1和0,要求给出不超过K次将0变成1的最长连续1数组。
这题目也可以解读为:给一个全是0和1的数组,求出不超过K个0的最长连续子序列的长度。
这里一开始的动态规划那里i & 1我看不懂,还有那个三元运算符也有点晕:dp[i][j]表示[i,j]最长的包含不超过K个0的连续1序列。
class Solution {
public int longestOnes(int[] nums, int k) {
int n = nums.length;
//
int[][] f = new int[2][k + 1];
int ans = 0;
for (int i = 1; i <= n; i++) {
for (int j = 0; j <= k; j++) {
if (nums[i - 1] == 1) {
f[i & 1][j] = f[(i - 1) & 1][j] + 1;
} else {
f[i & 1][j] = j == 0 ? 0 : f[(i - 1) & 1][j - 1] + 1;
}
ans = Math.max(ans, f[i & 1][j]);
}
}
return ans;
}
}
问了别人,说是i & 1可以判断奇偶,
这样相当于数组永远只储存当前和上一个的状态 节省空间
啊,,好吧。不过还是TLE超时了。
双指针是真的妙~利用右指针判断当前维护区间(左右指针)的0是否超出K个(长度-1的个数> k,1的个数就是区间和),一旦超出就左指针移,否则到达nums.length之前都是右指针移。
class Solution {
public int longestOnes(int[] nums, int k) {
//双指针,当指针区间包含不超过K个0时,右指针右移;当指针区间包含的0超过K时,左指针右移。这期间记录指针区间最大程度即为答案。
//简称:在作死边缘疯狂试探
//区间0不超过K个:right-left+1 - tot <= k 。tot是区间和,因为数组只有0和1,tot就是区间1的个数。
int max = 0;
int len = nums.length;
int tot = 0;
int right = 0,left = 0;
while(right < len){
tot+=nums[right];
if(right-left+1-tot <= k){
right++;
}
else{
tot -= nums[left];
left++;
}
max = max > right-left+1 ? max : right-left+1;
// System.out.println(max);
}
return max-1; //这里的-1我有点困惑,但是不减的话又过不去。。。
}
}
二分法:
当你知道答案的范围时,就可以利用二分法不断测试答案直到得出答案,最难的部分应该属于如何测试出答案是正确的。一般复杂度都在O(nlogn)。
题目:
难度困难
在一个 N x N 的坐标方格 grid 中,每一个方格的值 grid[i][j] 表示在位置 (i,j) 的平台高度。
现在开始下雨了。当时间为 t 时,此时雨水导致水池中任意位置的水位为 t 。你可以从一个平台游向四周相邻的任意一个平台,但是前提是此时水位必须同时淹没这两个平台。假定你可以瞬间移动无限距离,也就是默认在方格内部游动是不耗时的。当然,在你游泳的时候你必须待在坐标方格里面。
你从坐标方格的左上平台 (0,0) 出发。最少耗时多久你才能到达坐标方格的右下平台 (N-1, N-1)?
示例 1:
输入: [[0,2],[1,3]]
输出: 3
解释:
时间为0时,你位于坐标方格的位置为 (0, 0)。
此时你不能游向任意方向,因为四个相邻方向平台的高度都大于当前时间为 0 时的水位。
等时间到达 3 时,你才可以游向平台 (1, 1). 因为此时的水位是 3,坐标方格中的平台没有比水位 3 更高的,所以你可以游向坐标方格中的任意位置
示例2:
输入: [[0,1,2,3,4],[24,23,22,21,5],[12,13,14,15,16],[11,17,18,19,20],[10,9,8,7,6]]
输出: 16
解释:
0 1 2 3 4
24 23 22 21 5
12 13 14 15 16
11 17 18 19 20
10 9 8 7 6
最终的路线用加粗进行了标记。
我们必须等到时间为 16,此时才能保证平台 (0, 0) 和 (4, 4) 是连通的
提示:
2 <= N <= 50.grid[i][j]是[0, ..., N*N - 1]的排列。
这道困难题用二分竟然如此明了,只要题目给出了数据范围,就可以根据范围进行二分,然后思索如何写check函数(确定是不是那个分界点,也就是mid)即可。
check就是检查是否能在给定的mid时间内到达右下角那个终点。
这道题最困惑我的就是那个time,题解里直接“定格时间”,从初始状态开始判断<=time就为合法可移动位置。
check函数的方法是dfs,利用队列记录四个方位的值,然后对队列这些元素一个一个进行dfs。
class Solution {
int[][] dirs = new int[][]{{0,1},{0,-1},{1,0},{-1,0}};
public int swimInWater(int[][] grid) {
int n = grid.length;
int left = 0,right = n*n;
while(left < right){
int medium = (left+right)/2;
if(check(grid,medium)){
right = medium;
}
else{
left = medium+1;
}
}
return right;
}
//检查是否能在规定时间/步数内从左上角到达右下角
boolean check(int[][] grid,int time){
int n = grid.length;
Deque<int[]> queue = new ArrayDeque<>();//存储这次和下次坐标,同一个时刻队伍里只会存一个,而int[]表示坐标就只需要2个位子
boolean[][] visited = new boolean[n][n];//不能原路返回(这跟只能往下往右走没关系)
queue.push(new int[]{0,0});
visited[0][0] = true;
while(!queue.isEmpty()){
int[] from = queue.poll();
int x = from[0],y = from[1];
if(x==n-1 && y==n-1) return true;
for(int i = 0;i < 4;i++){
int newX = x + dirs[i][0],newY = y + dirs[i][1];
int[] to = new int[]{newX,newY};
if(inArea(n,newX,newY) && visited[newX][newY] == false && canMove(grid,from,to,time)){
queue.push(to);
visited[newX][newY] = true;
}
}
}
return false;
}
//判断x,y是否合法
boolean inArea(int n,int x,int y){
return x >= 0 && y >= 0 && x < n && y < n;
}
//判断所给时间是否足够
boolean canMove(int[][] grid,int[] from,int[] to,int time){
return time >= Math.max(grid[from[0]][from[1]],grid[to[0]][to[1]]);
}
}
所以注意:当要你求的答案有范围时,就可以尝试用二分,每次求出范围中点就验证下是否是要求的答案,这样思路会非常明了简单。
这题还有并查集的做法,但是三叶的文章需要先看另一篇专门讲并查集的文章:
(不过这题用图论肯定能做出来,二分是因为给了数据范围才可以用二分的。)
图论
图论也是并查集————无法用DP的(比如可以四周移动的,而不是只能向下和向右移动)尝试图论:
【综合笔试题】难度 3/5,为啥是图论不是 DP,两者是什么关系?
题目:
难度中等
你准备参加一场远足活动。给你一个二维 rows x columns 的地图 heights ,其中 heights[row][col] 表示格子 (row, col) 的高度。一开始你在最左上角的格子 (0, 0) ,且你希望去最右下角的格子 (rows-1, columns-1) (注意下标从 0 开始编号)。你每次可以往 上,下,左,右 四个方向之一移动,你想要找到耗费 体力 最小的一条路径。
一条路径耗费的 体力值 是路径上相邻格子之间 高度差绝对值 的 最大值 决定的。
请你返回从左上角走到右下角的最小 体力消耗值 。
示例 1:
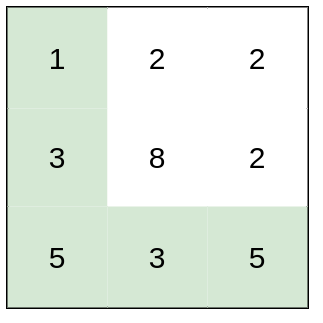
输入:heights = [[1,2,2],[3,8,2],[5,3,5]]
输出:2
解释:路径 [1,3,5,3,5] 连续格子的差值绝对值最大为 2 。
这条路径比路径 [1,2,2,2,5] 更优,因为另一条路径差值最大值为 3 。
示例 2:
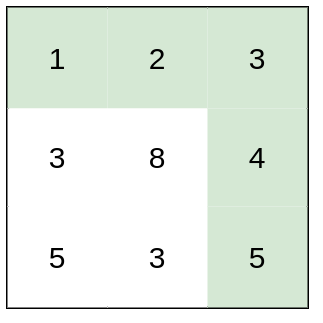
输入:heights = [[1,2,3],[3,8,4],[5,3,5]]
输出:1
解释:路径 [1,2,3,4,5] 的相邻格子差值绝对值最大为 1 ,比路径 [1,3,5,3,5] 更优。
示例 3:
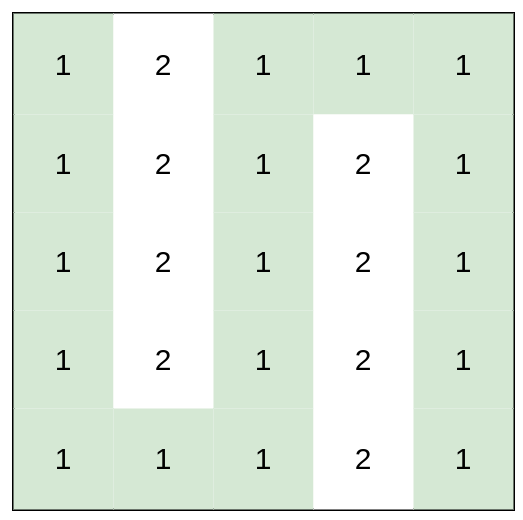
输入:heights = [[1,2,1,1,1],[1,2,1,2,1],[1,2,1,2,1],[1,2,1,2,1],[1,1,1,2,1]]
输出:0
解释:上图所示路径不需要消耗任何体力。
提示:
rows == heights.lengthcolumns == heights[i].length1 <= rows, columns <= 1001 <= heights[i][j] <= 106
文章中三叶说的区分DP和图论解法:
事实上,当题目允许往任意方向移动时,考察的往往就不是 DP 了,而是图论。
从本质上说,DP 问题是一类特殊的图论问题。
那为什么有一些 DP 题目简单修改条件后,就只能彻底转化为图论问题来解决了呢?
这是因为修改条件后,导致我们 DP 状态展开不再是一个拓扑序列,也就是我们的图不再是一个拓扑图。
换句话说,DP 题虽然都属于图论范畴。
但对于不是拓扑图的图论问题,我们无法使用 DP 求解。
而此类看似 DP,实则图论的问题,通常是最小生成树或者最短路问题。
我对于拓扑序列的理解是:前一个状态是固定死的,不会再变更。后一个状态依靠前一个固定死的状态得出,这样每一个状态都是正确的。拓扑排序也是每次取没有边指向的那个节点开始入手,因为“没人会管”,就可以先捏死这个节点(有点腹黑~)。
这题就是要走的最轻松,也就是求出最大高度差最小的路径,而不是求路程最短。
class Solution {
int row,col;
int[] p;
public int minimumEffortPath(int[][] heights) {
//这题二分我暂时想不到,先想图论(并查集)
//先把边全部放入并查集去,再升序排列,一条一条判断是否已经联通了左上角到右下角,一旦联通那当前边就是所要的最小的体力消耗值。
row = heights.length;
col = heights[0].length;
p = new int[row * col];//代表所以的点能到达的最终点,p[]整体代表当前联通情况,时刻都在变化当中
List<int[]> bingchaji = new ArrayList<>(); //[a,b,w]代表点a到点b的边(题目的图,每个点都能四个方向,实际只需要往右和往下,因为是无向边)
//预处理所有的点,p[i] = i表示点i当前能到达的点只有点i自己,p[i] = p表示存在路径使得i点->p点。
for(int i = 0;i < row * col;i++)p[i] = i;
//将边全部加入并查集
for(int i = 0;i < row;i++){
for(int j = 0;j < col;j++){
if(i + 1 < row){//将向下的边加入并查集
int a = getIndex(i,j),b = getIndex(i+1,j);
int w = Math.abs(heights[i][j]-heights[i+1][j]);
bingchaji.add(new int[]{a,b,w});
}
if(j + 1 < col){//将向右的边加入并查集
int a = getIndex(i,j),b = getIndex(i,j+1);
int w = Math.abs(heights[i][j]-heights[i][j+1]);
bingchaji.add(new int[]{a,b,w});
}
}
}
Collections.sort(bingchaji,(a,b)->a[2]-b[2]);
//对并查集的边一条一条边编辑p[],使得p[]代表当前联通情况
int start = getIndex(0,0),end = getIndex(row-1,col-1);
for(int[] ints : bingchaji){
int a = ints[0],b = ints[1],w = ints[2];
union(a,b);//联通边,更新p[]
if(query(start,end)){//如果当前已经首尾联通,w就是要求的值
return w;
}
}
return 0;
}
//判断当前首尾是否联通
boolean query(int start,int end){
return p[find(start)] == p[find(end)];
}
//将a、b点联通起来
void union(int a,int b){
p[find(a)] = p[find(b)];
}
//返回a当前能到达的点
int find(int a){
if(p[a] != a){
p[a] = find(p[a]);
}
return p[a];
}
//将二维坐标转换成一维的,比如(1,2)转成3,这样只需要一个数字就能代表坐标,这样坐标就会从左到右、从上到下排列起来。
//这样得到下边那个坐标就是getIndex(i+1,j);得到右边那个坐标就是getIndex(i,j+1)。
//(0,0),(0,1),(1,0),(1,1)就会变成0,1,2,3。
int getIndex(int i,int j){
return i * col + j;
}
}
路径问题专题
路径问题属于DP,而DP是特殊的图论问题。
这专题一定得拜读。
1. DP入门题
题目:
难度中等
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish” )。
问总共有多少条不同的路径?
示例 1:

输入:m = 3, n = 7
输出:28
示例 2:
输入:m = 3, n = 2
输出:3
解释:
从左上角开始,总共有 3 条路径可以到达右下角。
1. 向右 -> 向下 -> 向下
2. 向下 -> 向下 -> 向右
3. 向下 -> 向右 -> 向下
示例 3:
输入:m = 7, n = 3
输出:28
示例 4:
输入:m = 3, n = 3
输出:6
提示:
1 <= m, n <= 100- 题目数据保证答案小于等于
2 * 109
class Solution {
public int uniquePaths(int m, int n) {
int[][] dp = new int[m][n];
dp[0][0] = 1;
for(int i = 0;i < m;i++){
for(int j = 0;j < n;j++){
if(i-1 >= 0 && j-1 >= 0){
dp[i][j] = dp[i][j-1] + dp[i-1][j];
}
else if(i-1 >= 0){
dp[i][j] = dp[i-1][j];
}
else if(j-1 >= 0){
dp[i][j] = dp[i][j-1];
}
}
}
return dp[m-1][n-1];
}
}
没啥好解释的。
2. DP入门题2
题目:
难度中等
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为“Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为“Finish”)。
现在考虑网格中有障碍物。那么从左上角到右下角将会有多少条不同的路径?

网格中的障碍物和空位置分别用 1 和 0 来表示。
示例 1:

输入:obstacleGrid = [[0,0,0],[0,1,0],[0,0,0]]
输出:2
解释:
3x3 网格的正中间有一个障碍物。
从左上角到右下角一共有 2 条不同的路径:
1. 向右 -> 向右 -> 向下 -> 向下
2. 向下 -> 向下 -> 向右 -> 向右
示例 2:

输入:obstacleGrid = [[0,1],[0,0]]
输出:1
提示:
m == obstacleGrid.lengthn == obstacleGrid[i].length1 <= m, n <= 100obstacleGrid[i][j]为0或1
class Solution { public int uniquePathsWithObstacles(int[][] obstacleGrid) { int m = obstacleGrid.length; int n = obstacleGrid[0].length; if(obstacleGrid[0][0]==1){//当初始位置就是阻碍物时,压根没法出发,直接返回0. return 0; } int[][] dp = new int[m][n]; dp[0][0] = 1; for(int i = 0;i < m;i++){ for(int j = 0;j < n;j++){ if(obstacleGrid[i][j] == 1){ continue; } if(i-1 >= 0 && j-1 >= 0){ dp[i][j] = dp[i][j-1] + dp[i-1][j]; } else if(i-1 >= 0){ dp[i][j] = dp[i-1][j]; } else if(j-1 >= 0){ dp[i][j] = dp[i][j-1]; } } } return dp[m-1][n-1]; }}
3.最小路径和和两个进阶问题
题目:
难度中等
给定一个包含非负整数的 *m* x *n* 网格 grid ,请找出一条从左上角到右下角的路径,使得路径上的数字总和为最小。
说明:每次只能向下或者向右移动一步。
示例 1:

输入:grid = [[1,3,1],[1,5,1],[4,2,1]]输出:7解释:因为路径 1→3→1→1→1 的总和最小。
示例 2:
输入:grid = [[1,2,3],[4,5,6]]输出:12
提示:
m == grid.lengthn == grid[i].length1 <= m, n <= 2000 <= grid[i][j] <= 100
class Solution {
public int minPathSum(int[][] grid) {
int m = grid.length;
int n = grid[0].length;
int[][] dp = new int[m][n];
dp[0][0] = grid[0][0];
for(int i = 0;i < m;i++){
for(int j = 0;j < n;j++){
if(i-1 >= 0 && j-1 >= 0){
dp[i][j] = Math.min(dp[i][j-1],dp[i-1][j])+grid[i][j];
}
else if(i-1 >= 0){
dp[i][j] = dp[i-1][j]+grid[i][j];
}
else if(j-1 >= 0){
dp[i][j] = dp[i][j-1]+grid[i][j];
}
}
}
return dp[m-1][n-1];
}
}
dp[i][j]表示(0,0)到(i,j)总和最小值。
要是想求出这个最小路径(如果有重复的那就任选一个路径输出),或者有负权呢?后者只能用图论。
想求出最小路径,需要借助一维数组:
class Solution {
int m, n;
public int minPathSum(int[][] grid) {
m = grid.length;
n = grid[0].length;
int[][] f = new int[m][n];
int[] g = new int[m * n];
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (i == 0 && j == 0) {
f[i][j] = grid[i][j];
} else {
int top = i - 1 >= 0 ? f[i - 1][j] + grid[i][j] : Integer.MAX_VALUE;
int left = j - 1 >= 0 ? f[i][j - 1] + grid[i][j] : Integer.MAX_VALUE;
f[i][j] = Math.min(top, left);
//g[]记录的是上一步,由于i和j不一定是所要的地址,所以无法输出当前i和j来确定路径
g[getIdx(i, j)] = top < left ? getIdx(i - 1, j) : getIdx(i, j - 1);
}
}
}
// 从「结尾」开始,在 g[] 数组中找「上一步」
int idx = getIdx(m - 1, n - 1);
// 逆序将路径点添加到 path 数组中
int[][] path = new int[m + n][2];
path[m + n - 1] = new int[]{m - 1, n - 1};
for (int i = 1; i < m + n; i++) {
path[m + n - 1 - i] = parseIdx(g[idx]);
idx = g[idx];
}
// 顺序输出位置
for (int i = 1; i < m + n; i++) {
int x = path[i][0], y = path[i][1];
System.out.print("(" + x + "," + y + ") ");
}
System.out.println(" ");
return f[m - 1][n - 1];
}
int[] parseIdx(int idx) {
return new int[]{idx / n, idx % n};
}
int getIdx(int x, int y) {
return x * n + y;
}
}
4. 三角形的最小路径和(降低DP所需空间)
题目:
难度中等
给定一个三角形 triangle ,找出自顶向下的最小路径和。
每一步只能移动到下一行中相邻的结点上。相邻的结点 在这里指的是 下标 与 上一层结点下标 相同或者等于 上一层结点下标 + 1 的两个结点。也就是说,如果正位于当前行的下标 i ,那么下一步可以移动到下一行的下标 i 或 i + 1 。
示例 1:
输入:triangle = [[2],[3,4],[6,5,7],[4,1,8,3]]
输出:11
解释:如下面简图所示:
2
3 4
6 5 7
4 1 8 3
自顶向下的最小路径和为 11(即,2 + 3 + 5 + 1 = 11)。
示例 2:
输入:triangle = [[-10]]输出:-10
提示:
1 <= triangle.length <= 200triangle[0].length == 1triangle[i].length == triangle[i - 1].length + 1-104 <= triangle[i][j] <= 104
进阶:
- 你可以只使用
O(n)的额外空间(n为三角形的总行数)来解决这个问题吗?
O(n^2)的空间复杂度DP解法:
class Solution { //(0,0) //(1,0),(1,1) //(2,0),(2,1),(2,2) public int minimumTotal(List<List<Integer>> triangle) { int row = triangle.size(); int[][] dp = new int[row][row]; dp[0][0] = triangle.get(0).get(0); for(int i = 1;i < row;i++){ for(int j = 0;j <= i;j++){ if(j-1 >= 0 && j+1 <= i){ dp[i][j] = Math.min(dp[i-1][j],dp[i-1][j-1])+triangle.get(i).get(j); } else if(j - 1 >= 0){ dp[i][j] = dp[i-1][j-1]+triangle.get(i).get(j); } else if(j+1 <= i){ dp[i][j] = dp[i-1][j]+triangle.get(i).get(j); } } } int min = Integer.MAX_VALUE; for(int i = 0;i < row;i++){ min = min > dp[row-1][i] ? dp[row-1][i] : min; // System.out.println(dp[row-1][i]); } return min; }}
O(n)的空间复杂度解法:
此状态等上一某个状态的转化,那么要么等于左上角的+val,要么等于右上角+val,所以只需要2维。(前提是有左上角/右上角)
class Solution {
//(0,0)
//(1,0),(1,1)
//(2,0),(2,1),(2,2)
public int minimumTotal(List<List<Integer>> triangle) {
int row = triangle.size();
int[][] dp = new int[2][row];//此状态等上一某个状态的转化,那么要么等于左上角的+val,要么等于右上角+val,所以只需要2维。(前提是有左上角/右上角)
dp[0][0] = triangle.get(0).get(0);
for(int i = 1;i < row;i++){//从第二行开始,像[0][0]这种没爹没妈的特殊处理
for(int j = 0;j <= i;j++){
if(j-1 >= 0 && j+1 <= i){
dp[i%2][j] = Math.min(dp[(i-1)%2][j],dp[(i-1)%2][j-1])+triangle.get(i).get(j);
}
else if(j - 1 >= 0){
dp[i%2][j] = dp[(i-1)%2][j-1]+triangle.get(i).get(j);
}
else if(j+1 <= i){
dp[i%2][j] = dp[(i-1)%2][j]+triangle.get(i).get(j);
}
}
}
int min = Integer.MAX_VALUE;
for(int i = 0;i < row;i++){
min = min > dp[(row-1)%2][i] ? dp[(row-1)%2][i] : min;
// System.out.println(dp[row%2][i]);
}
return min;
}
}
当前状态如果是奇数行的dp,那么上一个状态就是偶数行的dp;反之同理。这样就只需要2*row的dp数组,空间复杂度O(n)。
5. 下降路径最小和
题目:
难度中等
给你一个 n x n 的 方形 整数数组 matrix ,请你找出并返回通过 matrix 的下降路径 的 最小和 。
下降路径 可以从第一行中的任何元素开始,并从每一行中选择一个元素。在下一行选择的元素和当前行所选元素最多相隔一列(即位于正下方或者沿对角线向左或者向右的第一个元素)。具体来说,位置 (row, col) 的下一个元素应当是 (row + 1, col - 1)、(row + 1, col) 或者 (row + 1, col + 1) 。
示例 1:
输入:matrix = [[2,1,3],[6,5,4],[7,8,9]]
输出:13
解释:下面是两条和最小的下降路径,用加粗标注:
[[2,1,3], [[2,1,3],
[6,5,4], [6,5,4],
[7,8,9]] [7,8,9]]
示例 2:
输入:matrix = [[-19,57],[-40,-5]]
输出:-59
解释:下面是一条和最小的下降路径,用加粗标注:
[[-19,57],
[-40,-5]]
示例 3:
输入:matrix = [[-48]]
输出:-48
提示:
n == matrix.lengthn == matrix[i].length1 <= n <= 100-100 <= matrix[i][j] <= 100
这题也是用dp异常简单,而且结合了上面提到的dp空间优化,现在只需要O(n^2)时间复杂度和O(n)空间复杂度:
class Solution {
public int minFallingPathSum(int[][] matrix) {
//dp[i][j]可能是dp[i-1][j]、dp[i-1][j-1]、dp[i-1][j+1],加上val而来
int n = matrix.length;
int[][] dp = new int[2][n];
for(int i = 0;i < n;i++){
dp[0][i] = matrix[0][i];
}
for(int i = 1;i < n;i++){
for(int j = 0;j < n;j++){
if(j-1 >= 0 && j+1 < n){
int min = Math.min(dp[(i-1)%2][j-1],dp[(i-1)%2][j]);
dp[i%2][j] = Math.min(min,dp[(i-1)%2][j+1]) + matrix[i][j];
}
else if(j-1 >= 0){
dp[i%2][j] = Math.min(dp[(i-1)%2][j-1],dp[(i-1)%2][j]) + matrix[i][j];
}
else if(j+1 < n){
dp[i%2][j] = Math.min(dp[(i-1)%2][j+1],dp[(i-1)%2][j]) + matrix[i][j];
}
}
}
int min = Integer.MAX_VALUE;
for(int i = 0;i < n;i++){
min = min > dp[(n-1)%2][i] ? dp[(n-1)%2][i] : min;
}
return min;
}
}
6. 下降路径最小和2()
题目:
难度困难
给你一个整数方阵 arr ,定义「非零偏移下降路径」为:从 arr 数组中的每一行选择一个数字,且按顺序选出来的数字中,相邻数字不在原数组的同一列。
请你返回非零偏移下降路径数字和的最小值。
示例 1:
输入:arr = [[1,2,3],[4,5,6],[7,8,9]]
输出:13
解释:
所有非零偏移下降路径包括:
[1,5,9], [1,5,7], [1,6,7], [1,6,8],
[2,4,8], [2,4,9], [2,6,7], [2,6,8],
[3,4,8], [3,4,9], [3,5,7], [3,5,9]
下降路径中数字和最小的是 [1,5,7] ,所以答案是 13 。
提示:
1 <= arr.length == arr[i].length <= 200-99 <= arr[i][j] <= 99
就这?hard难度?(doge
class Solution {
public int minFallingPathSum(int[][] arr) {
int n = arr.length;
int[][] dp = new int[2][n];
for(int i = 0;i < n;i++){
dp[0][i] = arr[0][i];
}
for(int i = 1;i < n;i++){
for(int j = 0;j < n;j++){
int min = Integer.MAX_VALUE;
for(int z = 0;z < n;z++){ //这里也可以进行排序然后取第一个元素,用sort的话可以做到O(n^2logn)
if(z == j)continue;
min = min > dp[(i-1)%2][z] ? dp[(i-1)%2][z] : min;
}
dp[i%2][j] = min + arr[i][j];
}
}
int min = Integer.MAX_VALUE;
for(int i = 0;i < n;i++){
min = min > dp[(n-1)%2][i] ? dp[(n-1)%2][i] : min;
}
return min;
}
}
但是注意上述解法虽然思路简单,但是时间复杂度高达O(n^3),一旦数组长度超过1000就会超时,所以要优化到O(n^2)。
7. 【动态规划/路径问题】「动态规划」的前置思考「记忆化搜索」,以及如何推导基本性质来简化 Base Case ...
题目
难度困难
给你一个 互不相同 的整数数组,其中 locations[i] 表示第 i 个城市的位置。同时给你 start,finish 和 fuel 分别表示出发城市、目的地城市和你初始拥有的汽油总量
每一步中,如果你在城市 i ,你可以选择任意一个城市 j ,满足 j != i 且 0 <= j < locations.length ,并移动到城市 j 。从城市 i 移动到 j 消耗的汽油量为 |locations[i] - locations[j]|,|x| 表示 x 的绝对值。
请注意, fuel 任何时刻都 不能 为负,且你 可以 经过任意城市超过一次(包括 start 和 finish )。
请你返回从 start 到 finish 所有可能路径的数目。
由于答案可能很大, 请将它对 10^9 + 7 取余后返回。
示例 1:
输入:locations = [2,3,6,8,4], start = 1, finish = 3, fuel = 5
输出:4
解释:以下为所有可能路径,每一条都用了 5 单位的汽油:
1 -> 3
1 -> 2 -> 3
1 -> 4 -> 3
1 -> 4 -> 2 -> 3
示例 2:
输入:locations = [4,3,1], start = 1, finish = 0, fuel = 6
输出:5
解释:以下为所有可能的路径:
1 -> 0,使用汽油量为 fuel = 1
1 -> 2 -> 0,使用汽油量为 fuel = 5
1 -> 2 -> 1 -> 0,使用汽油量为 fuel = 5
1 -> 0 -> 1 -> 0,使用汽油量为 fuel = 3
1 -> 0 -> 1 -> 0 -> 1 -> 0,使用汽油量为 fuel = 5
示例 3:
输入:locations = [5,2,1], start = 0, finish = 2, fuel = 3
输出:0
解释:没有办法只用 3 单位的汽油从 0 到达 2 。因为最短路径需要 4 单位的汽油。
示例 4 :
输入:locations = [2,1,5], start = 0, finish = 0, fuel = 3
输出:2
解释:总共有两条可行路径,0 和 0 -> 1 -> 0 。
示例 5:
输入:locations = [1,2,3], start = 0, finish = 2, fuel = 40
输出:615088286
解释:路径总数为 2615088300 。将结果对 10^9 + 7 取余,得到 615088286 。
提示:
2 <= locations.length <= 1001 <= locations[i] <= 10^9- 所有
locations中的整数 互不相同 。 0 <= start, finish < locations.length1 <= fuel <= 200
不愧是困难题,题目一开始居然读不懂,还以为是locattion[]表示城市位置......结果是“汽油绝对值”,而location[]的下标才表示城市位置。
由于要搜索可能的全部解,我想到了递归。
class Solution {
int resnum = 0;
List<List<Integer>> temp = new ArrayList<>();
public int countRoutes(int[] locations, int start, int finish, int fuel) {
int len = locations.length;
backroll(locations,start,finish,fuel,len,new ArrayList<>());
for(int i = 0;i < temp.size();i++){
for(int j = 0;j < temp.get(i).size();j++)
System.out.print(temp.get(i).get(j)+" ");
System.out.println();
}
return resnum;
}
void backroll(int[] locations, int start, int finish, int fuel,int len,List<Integer> temp2){
if(start == finish ){
resnum++;
temp.add(new ArrayList<>(temp2));
return;
}
if(start >= len){
return;
}
//finish可能在start前面也可能在start后面
for(int i = start;i < len;i++){
if(i == start || Math.abs(locations[i] - locations[start]) > fuel){
continue;
}
temp2.add(i);
//如果这里不需要记录路径,只需要路径数,那么不需要撤销操作什么的
backroll(locations,i,finish,fuel-Math.abs(locations[i] - locations[start]),len,temp2);
temp2.remove(temp2.size()-1);
}
for(int i = 0;i < start;i++){
if(i == start || Math.abs(locations[i] - locations[start]) > fuel){
continue;
}
temp2.add(i);
backroll(locations,i,finish,fuel-Math.abs(locations[i] - locations[start]),len,temp2);
temp2.remove(temp2.size()-1);
}
}
}
但是这样的模板写出来却忽略了题目说的可以重复走的情况,也就是到达目的城市后如果油没有用完,那么可以往其他地方逛直至最后回到目的地。这样就需要重新考虑递归终止的情况(上面就是只考虑了start到达finish的情况,也就是第一次到达目的地的时候就立即终止递归了)。
一开始以为如果要考虑是否还有城市可以凭借现有油量到达,那就要遍历一遍当前城市到剩下城市的所有油耗。
但是我错了,其实只要start和finish相等时不终止,一相等就达成一个路径,等到start>length时才终止即可。
class Solution {
int resnum = 0;
List<List<Integer>> temp = new ArrayList<>();
public int countRoutes(int[] locations, int start, int finish, int fuel) {
int len = locations.length;
backroll(locations,start,finish,fuel,len,new ArrayList<>());
// for(int i = 0;i < temp.size();i++){
// for(int j = 0;j < temp.get(i).size();j++)
// System.out.print(temp.get(i).get(j)+" ");
// System.out.println();
// }
return resnum;
}
void backroll(int[] locations, int start, int finish, int fuel,int len,List<Integer> temp2){
if(start == finish ){
resnum++;
temp.add(new ArrayList<>(temp2));
// boolean flag = false;
// for(int i = 0;i < len;i++){
// if(fuel < Math.abs(locations[i] - locations[finish])){
// flag = true;
// break;
// }
// }
// if(flag){
// resnum++;
// temp.add(new ArrayList<>(temp2));
// }
}
if(start >= len){
return;
}
//finish可能在start前面也可能在start后面
for(int i = start;i < len;i++){
if(i == start || Math.abs(locations[i] - locations[start]) > fuel){
continue;
}
temp2.add(i);
//如果这里不需要记录路径,只需要路径数,那么不需要撤销操作什么的
backroll(locations,i,finish,fuel-Math.abs(locations[i] - locations[start]),len,temp2);
temp2.remove(temp2.size()-1);
}
for(int i = 0;i < start;i++){
if(i == start || Math.abs(locations[i] - locations[start]) > fuel){
continue;
}
temp2.add(i);
backroll(locations,i,finish,fuel-Math.abs(locations[i] - locations[start]),len,temp2);
temp2.remove(temp2.size()-1);
}
}
}
问题又来了,在以下例子超限:
执行结果:超出内存限制
最后执行的输入:[1,2,3] 0 2 40
当油量达到40时就超出内存限制了(如果你以为是由于那个temp数组导致的超限那么你跟我一样想的,去掉之后就变成超出时间限制......)。所以必须加个记忆化搜索,这一加就相当于是dp了。
class Solution {
int mod = 1000000007;
int[][] dp;
public int countRoutes(int[] locations, int start, int finish, int fuel) {
int len = locations.length;
dp = new int[len][fuel+1];//[i][j]表示当前在i城市,油量为j,能到达finish城市的路径数。注意这里其实不是完全的dp,因为他仅仅起到记录作用,而不是最终答案,只是形式化类似于动态规划dp,所以取名叫dp。-1表示此状态未计算过,0表示没有路径,>0表示路径数
for(int i = 0;i < len;i++){
Arrays.fill(dp[i],-1);
}
return backroll(locations,start,finish,fuel,len);
}
int backroll(int[] locations, int start, int finish, int fuel,int len){
//三种情况是递归终止条件
//情况1:直接查得到
if(dp[start][fuel] != -1){
return dp[start][fuel];
}
//情况2:查不到的基础上,油量耗尽,但还未到达目的地
if(start != finish && fuel == 0){
dp[start][fuel] = 0;
return 0;
}
//情况3:查不到的基础上,剩余油量没有够去任何一座城市,本身也不是目的地
boolean flag = false;
for(int i = 0;i < len;i++){
if(i == start) continue;
if(fuel >= Math.abs(locations[start] - locations[i])) {
flag = true;
break;
}
}
if(fuel != 0 && flag == false){
dp[start][fuel] = start == finish ? 1 : 0;
return dp[start][fuel];
}
//情况4:需要继续递归的情况,油量充足到下一座城市,并且目前还没到目的地
int sum = start == finish ? 1 : 0;
for(int i = 0;i < len;i++){
if(i == start)continue;
if(fuel >= Math.abs(locations[start] - locations[i])){
sum += backroll(locations,i,finish,fuel - Math.abs(locations[start] - locations[i]),len);
sum %= mod;
}
}
dp[start][fuel] = sum;
return sum;
}
}







 浙公网安备 33010602011771号
浙公网安备 33010602011771号