胡乱的刷题记录
- 回溯
- 动态规划
- 每日一题
- 栈,逆波兰表达式
- 动态规划
- 1143. 最长公共子序列
- 461. 汉明距离
- 781. 森林中的兔子
- 88. 合并两个有序数组
- 80. 删除有序数组中的重复项 II
- 81. 搜索旋转排序数组 II
- 153. 寻找旋转排序数组中的最小值
- 154. 寻找旋转排序数组中的最小值 II
- 263. 丑数
- 264. 丑数 II
- 179. 最大数
- 783. 二叉搜索树节点最小距离
- 208. 实现 Trie (前缀树)
- 213. 打家劫舍 II
- 87. 扰乱字符串
- 220. 存在重复元素 III
- 26. 删除有序数组中的重复项
- 27. 移除元素
- 28. 实现 strStr()
- 91. 解码方法
- 363. 矩形区域不超过 K 的最大数值和
- 368. 最大整除子集
- 377. 组合总和 Ⅳ
- 897. 递增顺序搜索树
- 1011. 在 D 天内送达包裹的能力
- Top100
回溯
选择困难症?回溯!
回溯的核心是递归,递归里面暴力枚举+剪枝。递归也是空间换时间的一种,跟查表法相似但是不一样。
-
1688. 比赛中的配对次数
难度简单
给你一个整数
n,表示比赛中的队伍数。比赛遵循一种独特的赛制:- 如果当前队伍数是 偶数 ,那么每支队伍都会与另一支队伍配对。总共进行
n / 2场比赛,且产生n / 2支队伍进入下一轮。
- 如果当前队伍数是 偶数 ,那么每支队伍都会与另一支队伍配对。总共进行
-
如果当前队伍数为 奇数 ,那么将会随机轮空并晋级一支队伍,其余的队伍配对。总共进行
(n - 1) / 2场比赛,且产生(n - 1) / 2 + 1支队伍进入下一轮。返回在比赛中进行的配对次数,直到决出获胜队伍为止。
class Solution { public int numberOfMatches(int n) { return times(n); } public int times(int n){ if(n <= 1) return 0; if(n % 2 == 0){ return n/2 + times(n/2); } else{ return (n-1)/2+times((n-1)/2+1); } } }
-
面试题 08.04. 幂集
难度中等
幂集。编写一种方法,返回某集合的所有子集。集合中不包含重复的元素。
说明:解集不能包含重复的子集。
示例:
输入: nums = [1,2,3] 输出: [ [3], [1], [2], [1,2,3], [1,3], [2,3], [1,2], [] ]非递归解法:
这里有毒的是,1处如果不是result.size()放在for(a;b;c)的a,会造成时间超限,i是有必要的。加了后直接1ms解决。
class Solution { public List<List<Integer>> subsets(int[] nums) { //非递归 List<List<Integer>> result = new ArrayList<>(); result.add(new ArrayList<>()); for(int num:nums){ for(int j = 0,i = result.size();j < i;j++){ // 1 List<Integer> temp = new ArrayList<>(result.get(j)); temp.add(num); result.add(temp); } } return result; } }递归解法:
记模板,for循环里,做选择->递归->撤销选择。撤销是防止分支污染。
模板:
private void backtrack("原始参数") { //终止条件(递归必须要有终止条件)或者是一些判断 for (int i = "for循环开始的参数"; i < "for循环结束的参数"; i++) { //一些逻辑操作(可有可无,视情况而定) //做出选择 //递归 backtrack("新的参数"); //一些逻辑操作(可有可无,视情况而定) //撤销选择,防止分支污染(参考n叉树回溯) } } 作者:sdwwld 链接:https://leetcode-cn.com/problems/power-set-lcci/solution/hui-su-wei-yun-suan-deng-gong-4chong-fang-shi-jie-/ 来源:力扣(LeetCode) 著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。class Solution { List<List<Integer>> result = new ArrayList<>(); public List<List<Integer>> subsets(int[] nums) { //递归,看成n叉树 backroll(result,new ArrayList<Integer>(),nums,0); return result; } public void backroll(List<List<Integer>> result,List<Integer> temp,int[] nums,int start){ result.add(new ArrayList<>(temp)); for(int i = start;i < nums.length;i++){ temp.add(nums[i]); backroll(result,temp,nums,i+1); temp.remove(temp.size() - 1); //1 } } } -
面试题 08.09. 括号
难度中等
括号。设计一种算法,打印n对括号的所有合法的(例如,开闭一一对应)组合。
说明:解集不能包含重复的子集。
例如,给出 n = 3,生成结果为:
[ "((()))", "(()())", "(())()", "()(())", "()()()" ]没有图居然也能用dfs,这让我明白只要是数组都可以用dfs,得抽象成数组是n叉树的遍历结果。
递归就是递和归——递进、回归,每次都会进一步,调完就会退回原处。
class Solution { List<String> result = new ArrayList<>(); public List<String> generateParenthesis(int n) { //递归 dfs(0,0,n,""); return result; } public void dfs(int left,int right,int n,String temp){ if(left == n && right == n) { result.add(temp); return; } if(left > n || right > n){ return; } if(right > left){ return; } dfs(left+1,right,n,temp+"("); dfs(left,right+1,n,temp+")"); } } -
面试题 08.07. 无重复字符串的排列组合
难度中等
无重复字符串的排列组合。编写一种方法,计算某字符串的所有排列组合,字符串每个字符均不相同。
示例1:
输入:S = "qwe" 输出:["qwe", "qew", "wqe", "weq", "ewq", "eqw"]示例2:
输入:S = "ab" 输出:["ab", "ba"]提示:
- 字符都是英文字母。
- 字符串长度在[1, 9]之间。
1处是为了去重(“qqq”、“qqw”这样的结果),后来发现超时。2处刚开始写成了return,结果过度剪枝(比如输入“qwe”,你是q开始,要选择q还是w还是e,选择q直接return,那就没有qwe和qew的结果了)。
class Solution { public String[] permutation(String S) { List<String> result = new ArrayList<>(); backroll(S,"",result,0); return result.toArray(new String[result.size()]); } public void backroll(String S,String temp,List<String> result,int start){ if(temp.length() == S.length()){ // System.out.println(temp); // for(int i = 0,j = temp.length();i < j;i++){ // 1 // String temp01 = temp.replaceAll(temp.charAt(i)+"",""); // if(temp01.length() != temp.length()-1){ // return; // } // } result.add(temp); return; } for(int i = 0,j = S.length();i < j;i++){ if(temp.contains(S.charAt(i)+"")) continue; // 2 temp = temp+S.charAt(i); backroll(S,temp,result,i+1); temp = temp.substring(0,temp.length() -1); } } } //题解里别人的简洁答案 class Solution { List<String> list= new ArrayList<>(); StringBuffer s=new StringBuffer(); public String[] permutation(String S) { dfs(S,list,s); return list.toArray(new String[list.size()]); } public void dfs(String S,List<String> list,StringBuffer s) { if(s.length() == S.length()){ list.add(new String(s)); return; } for(int i=0;i<S.length();i++){ String zz=new String(s); if(zz.contains(S.charAt(i)+"")){ continue; } s.append(S.charAt(i)); dfs(S,list,s); s.deleteCharAt(s.length()-1); } } } 作者:Qiumg 链接:https://leetcode-cn.com/problems/permutation-i-lcci/solution/java-wu-zhong-fu-zi-fu-chuan-pai-lie-by-wqyyi/ 来源:力扣(LeetCode) 著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。String[]只能存放String格式数据,而且一般的是固定大小长度的;
List指的是集合,<>是泛型,里面存放一个实体类可以是String,int或者自定义的;
Listlist=new List ();
String为你想要的对象,里面可以有属性,方法等,这就是面向对象。
而String[]只是存放值而已,不是对象String[]是数组,定长,不可变
List<String> 是泛型 ,非定长,可变String[]转List<String>
String[] arr = new String[]{"s1","s2","s3"}; List<String> list = Arrays.asList(arr); List<String>转String[]List
转String[] List<String> list = new ArrayList<String>(); list.add("s1"); list.add("s2"); list.add("s3"); String[] arr = list.toArray(new String[list.size()]);
版权声明:本文为CSDN博主「chpllp」的原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接及本声明。
原文链接:https://blog.csdn.net/chpllp/article/details/83819941 -
77. 组合
难度中等
给定两个整数 n 和 k,返回 1 ... n 中所有可能的 k 个数的组合。
示例:
输入: n = 4, k = 2 输出: [ [2,4], [3,4], [2,3], [1,2], [1,3], [1,4], ]做了几道回溯题下来我的感觉就是建模成n叉树,做选择->n叉树(二叉树还可以只做两个选择)->dfs。
这题我的思路是n叉树(for循环n次),k层(递归k次)。
注意1处的二维数组的格式,不然result将会是[[],[],[]];2处不要搞成nums.remove(num[j])或者remove(j),因为j不一定是最后一个数组的下标。
class Solution { public List<List<Integer>> combine(int n, int k) { List<List<Integer>> result = new ArrayList<>(); backroll(1,n,k,new ArrayList<Integer>(),result); return result; } public void backroll(int start,int n,int k,List<Integer> nums,List<List<Integer>> result){ if(nums.size() == k){ result.add(new ArrayList<>(nums)); //1 return; } for(int j = start;j <= n;j++){ nums.add(j); backroll(j+1,n,k,nums,result); nums.remove(nums.size()-1); //2 // System.out.println(Arrays.asList(nums)); } } }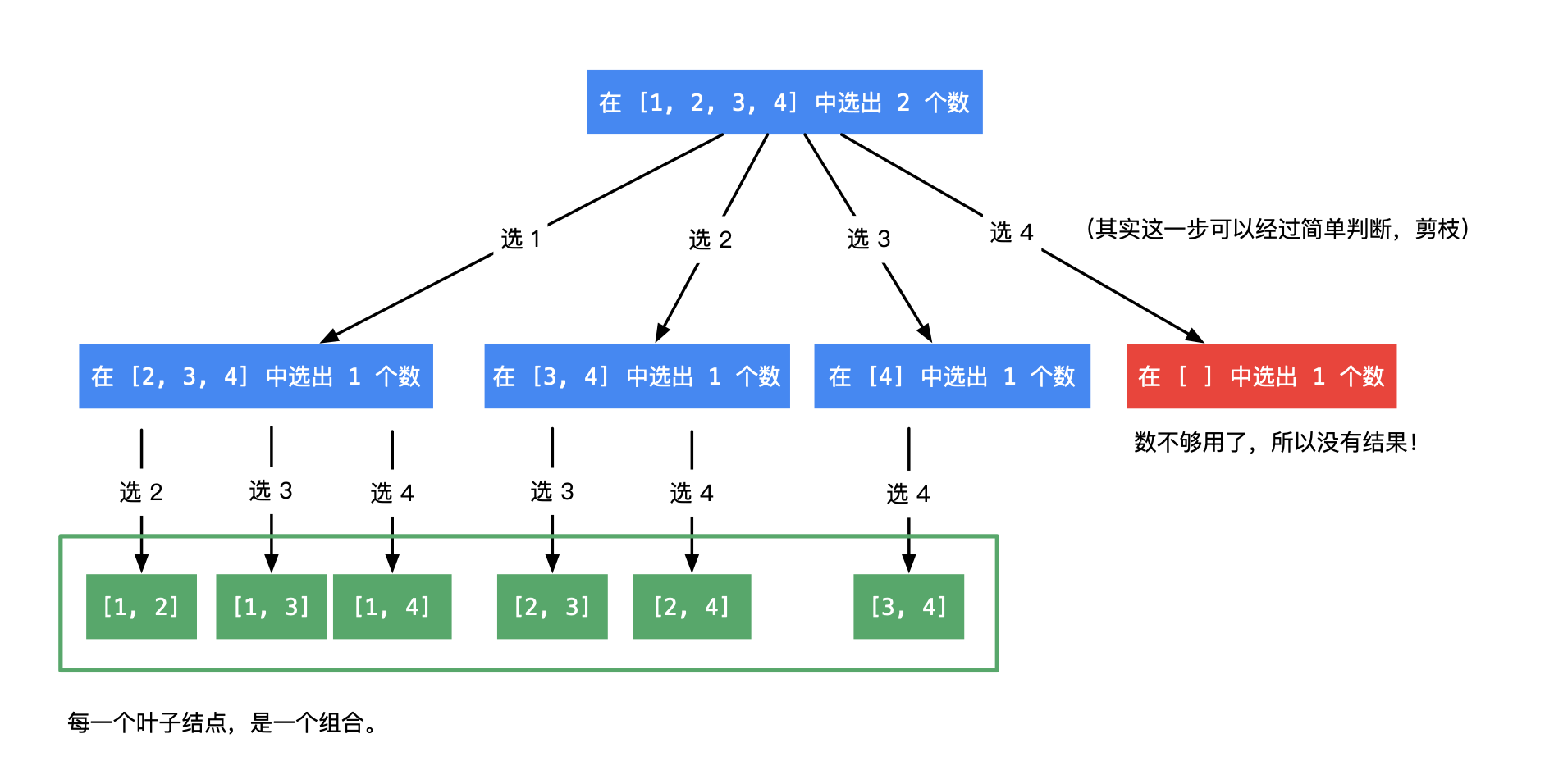
图片来自leetcode,这是很好的一张回溯图。
-
216. 组合总和 III
难度中等
找出所有相加之和为 n 的 k 个数的组合。组合中只允许含有 1 - 9 的正整数,并且每种组合中不存在重复的数字。
说明:
- 所有数字都是正整数。
- 解集不能包含重复的组合。
示例 1:
输入: k = 3, n = 7 输出: [[1,2,4]]示例 2:
输入: k = 3, n = 9 输出: [[1,2,6], [1,3,5], [2,3,4]]模板方便且高效,可是边界值不注意就会出错。记住n仅仅是判断递归终止条件,k是递归次数也是判断递归终止条件,9是叉数。也即9叉树,k层。
class Solution { public List<List<Integer>> combinationSum3(int k, int n) { List<List<Integer>> result = new ArrayList<>(); backtrack(1,0,k,n,result,new ArrayList<>()); return result; } public void backtrack(int i,int sum,int k,int n,List<List<Integer>> result,List<Integer> temp){ if(sum > n){ return; } if(temp.size() == k){ //1 if(sum == n){ result.add(new ArrayList<>(temp)); } return; } for(int j = i;j <= 9;j++){ //2 sum += j; temp.add(new Integer(j)); backtrack(j+1,sum,k,n,result,temp); sum -= j; temp.remove(temp.size()-1); } } } -
1079. 活字印刷
难度中等
你有一套活字字模
tiles,其中每个字模上都刻有一个字母tiles[i]。返回你可以印出的非空字母序列的数目。注意:本题中,每个活字字模只能使用一次。
示例 1:
输入:"AAB" 输出:8 解释:可能的序列为 "A", "B", "AA", "AB", "BA", "AAB", "ABA", "BAA"。示例 2:
输入:"AAABBC" 输出:188提示:
- `1 <= tiles.length <= 7``
- ``tiles` 由大写英文字母组成
这题跟普通回溯不一样,求幂集和求组合是不一样的,幂集要求集合成员不能全部一样,而组合则顺序不一样就可以算一个不同组合(AB和BA是两个组合),组合相同元素的不同位置也算一个组合(ABBCD和ABBCD,两个B调换了,但是属于一个组合结果)。
//下面的不是正确答案,可以输出求幂集的结果 /* 输入"ABC"时, 输出[[, A, AB, ABC, AC, B, BC, C]],8个子集 */ class Solution { static int sum = 0; List<String> result = new ArrayList<>(); public int numTilePossibilities(String tiles) { //非空子集 //递归 String temp = new String(); backtrack(0,tiles,temp,result); System.out.println(Arrays.asList(result)); return sum; } public void backtrack(int start,String tiles,String temp,List<String> result){ result.add(temp); sum += 1; if(start >= tiles.length()){ return; } for(int i = start;i < tiles.length();i++){ // System.out.println(i+"|"+tiles.charAt(i)); temp = temp+tiles.charAt(i); // System.out.println(i+temp); backtrack(i+1,tiles,temp,result); // System.out.println(i+temp); temp = temp.substring(0,temp.length()-1); // System.out.println(i+"-"+temp); } } } //题解里别人的答案 class Solution { public int numTilePossibilities(String tiles) { char[] chars = tiles.toCharArray(); //先排序,目的是让相同的字符挨着,在下面计算的时候好过滤掉重复的 Arrays.sort(chars); int[] res = new int[1]; backtrack(res, chars, new boolean[tiles.length()], tiles.length(), 0); return res[0]; } private void backtrack(int[] res, char[] chars, boolean[] used, int length, int index) { //如果没有可以选择的就返回 if (index == length) return; //注意,这里的i每次都是从0开始的,不是从index开始 for (int i = 0; i < length; i++) { //一个字符只能选择一次,如果当前字符已经选择了,就不能再选了。 if (used[i]) continue; //过滤掉重复的结果 if (i - 1 >= 0 && chars[i] == chars[i - 1] && !used[i - 1]) continue; //选择当前字符,并把它标记为已选择 used[i] = true; res[0]++;//选择一个字符,就多了一种结果 //下一分支继续递归 backtrack(res, chars, used, length, index + 1); //使用完之后再把它给复原。 used[i] = false; } } } -
797. 所有可能的路径
难度中等114收藏分享切换为英文关闭提醒反馈
给一个有
n个结点的有向无环图,找到所有从0到n-1的路径并输出(不要求按顺序)二维数组的第
i个数组中的单元都表示有向图中i号结点所能到达的下一些结点(译者注:有向图是有方向的,即规定了 a→b 你就不能从 b→a )空就是没有下一个结点了。示例 1:

输入:graph = [[1,2],[3],[3],[]] 输出:[[0,1,3],[0,2,3]] 解释:有两条路径 0 -> 1 -> 3 和 0 -> 2 -> 3class Solution { public List<List<Integer>> allPathsSourceTarget(int[][] graph) { List<List<Integer>> result = new ArrayList<>(); List<Integer> temp = new ArrayList<>(); temp.add(0); backtrack(0,graph,result,temp); return result; } public void backtrack(int start,int[][] graph,List<List<Integer>> result,List<Integer> temp){ if(start >= graph.length){ return; } if(temp.contains(graph.length-1)){ result.add(new ArrayList<>(temp)); //1 return; } for(int i = 0,j = graph[start].length;i < j;i++){ temp.add(graph[start][i]); // System.out.println(Arrays.asList(temp) +"|"+ (graph.length-1)+"|"+start); backtrack(graph[start][i],graph,result,temp); temp.remove(temp.size()-1); } } }1处老贼坑了,不加new ArrayList<>()就不给添加进result,也不报错。
-
51. N 皇后
难度困难
n 皇后问题 研究的是如何将
n个皇后放置在n×n的棋盘上,并且使皇后彼此之间不能相互攻击。给你一个整数
n,返回所有不同的 n 皇后问题 的解决方案。每一种解法包含一个不同的 n 皇后问题 的棋子放置方案,该方案中
'Q'和'.'分别代表了皇后和空位。示例 1:

输入:n = 4 输出:[[".Q..","...Q","Q...","..Q."],["..Q.","Q...","...Q",".Q.."]] 解释:如上图所示,4 皇后问题存在两个不同的解法。示例 2:
输入:n = 1 输出:[["Q"]]提示:
1 <= n <= 9- 皇后彼此不能相互攻击,也就是说:任何两个皇后都不能处于同一条横行、纵行或斜线上。
//看了官方题解后勉勉强强默写下来的题解... class Solution { public List<List<String>> solveNQueens(int n) { //回溯,空间换时间 List<List<String>> result = new ArrayList<>(); Set<Integer> columns = new HashSet<>(); Set<Integer> dias1 = new HashSet<>(); Set<Integer> dias2 = new HashSet<>(); int[] queens = new int[n]; Arrays.fill(queens,-1); backtrack(result,columns,dias1,dias2,0,n,queens); return result; } /** int[] queens:一个答案中的n个皇后对应的列序号数组[1,3,5]表示3x3棋盘上(1,1)、(2,3)、(3,5)放着皇后。 */ public void backtrack(List<List<String>> result,Set<Integer> columns,Set<Integer> dias1,Set<Integer> dias2,int row,int n,int[] queens){ if(row == n){//一旦row==n,表示当前递归的函数就是答案之一 //输出数组 List<String> board = generateboard(queens,n); result.add(board); }else{ for(int i = 0;i < n;i++){//i是列,row是行 if(columns.contains(i)){//正上方 continue; } int diastr1 = row - i;//左上角 if(dias1.contains(diastr1)){ continue; } int diastr2 = row + i;//右上角 if(dias2.contains(diastr2)){ continue; } queens[row] = i; columns.add(i); dias1.add(diastr1); dias2.add(diastr2); backtrack(result,columns,dias1,dias2,row+1,n,queens); queens[row] = -1; columns.remove(i); dias1.remove(diastr1); dias2.remove(diastr2); } } } /*将queens化成答案,输出诸如["..Q","Q.."]*/ public List<String> generateboard(int[] queens,int n){ List<String> board = new ArrayList<>(); for(int i = 0;i < n;i++){ char[] chars = new char[n]; Arrays.fill(chars,'.'); chars[queens[i]] = 'Q'; board.add(new String(chars)); } return board; } }
动态规划
建立状态数组,用空间换时间、查表法
-
面试题 16.17. 连续数列
难度简单
给定一个整数数组,找出总和最大的连续数列,并返回总和。
示例:
输入: [-2,1,-3,4,-1,2,1,-5,4] 输出: 6 解释: 连续子数组 [4,-1,2,1] 的和最大,为 6。class Solution { public int maxSubArray(int[] nums) { int now = 0,maxNums = nums[0]; // 1 for(int i : nums){ now = Math.max(now+i,i); maxNums = Math.max(maxNums,now); } return maxNums; } }这题要维护一个f(i),代表第i位结尾的最大值。然后求出f(0)~f(n-1)的最大值即是最大连续子列和。由于只要f()的最大值,所以只要一个now变量维护当前f(i),maxNums记录至今为止最大的f(i)即可。
注意1处maxNums不能初始化为0,因为[-1]最大和是-1不是0。
-
338. 比特位计数
难度中等
给定一个非负整数 num。对于 0 ≤ i ≤ num 范围中的每个数字 i ,计算其二进制数中的 1 的数目并将它们作为数组返回。
示例 1:
输入: 2 输出: [0,1,1]示例 2:
输入: 5 输出: [0,1,1,2,1,2]题解里看到的,偶数的1个数等于右移一位也就是除以2后的1的个数;奇数的1个数等于前一个偶数+1,因为就是个位上多出来的1。
class Solution { public int[] countBits(int num) { int[] result = new int[num+1]; result[0] = 0; for(int i = 0;i <= num;i++){ if(i % 2 == 0){ result[i] = result[i/2]; } else{ result[i] = result[i-1]+1; } } return result; } } -
1641. 统计字典序元音字符串的数目
难度中等
给你一个整数
n,请返回长度为n、仅由元音 (a,e,i,o,u) 组成且按 字典序排列 的字符串数量。字符串
s按 字典序排列 需要满足:对于所有有效的i,s[i]在字母表中的位置总是与s[i+1]相同或在s[i+1]之前。示例 1:
输入:n = 1 输出:5 解释:仅由元音组成的 5 个字典序字符串为 ["a","e","i","o","u"]示例 2:
输入:n = 2 输出:15 解释:仅由元音组成的 15 个字典序字符串为 ["aa","ae","ai","ao","au","ee","ei","eo","eu","ii","io","iu","oo","ou","uu"] 注意,"ea" 不是符合题意的字符串,因为 'e' 在字母表中的位置比 'a' 靠后示例 3:
输入:n = 33 输出:66045提示:
1 <= n <= 50
1处的51和6分别是提示的1<=n<=50和一共aeiou5个元音字母。result[n][0]表示长度为n、结尾字符为a的字符串;result[n][1]表示长度为n、结尾字符为e的字符串......result数组就是状态数组。
class Solution { public int countVowelStrings(int n) { int[][] result = new int[51][6]; // 1 result[1][0] = result[1][1] = result[1][2] = result[1][3] = result[1][4] = 1; for(int i = 2;i <= n;i++){ result[i][0] = result[i-1][0] + result[i-1][1] + result[i-1][2] + result[i-1][3] + result[i-1][4]; result[i][1] = result[i-1][1] +result[i-1][2] + result[i-1][3] + result[i-1][4]; result[i][2] = result[i-1][2] + result[i-1][3] + result[i-1][4]; result[i][3] = result[i-1][3] + result[i-1][4]; result[i][4] = result[i-1][4]; } return result[n][0]+ result[n][1]+ result[n][2]+ result[n][3]+ result[n][4]; } } -
131. 分割回文串
难度中等
给你一个字符串
s,请你将s分割成一些子串,使每个子串都是 回文串 。返回s所有可能的分割方案。回文串 是正着读和反着读都一样的字符串。
示例 1:
输入:s = "aab" 输出:[["a","a","b"],["aa","b"]]示例 2:
输入:s = "a" 输出:[["a"]]提示:
1 <= s.length <= 16s仅由小写英文字母组成
//这题不是动态规划做的,而是回溯,但是回溯的套路这里有一点变更,比如没有start了,毕竟题目要求的是所有可能方案。 class Solution { public List<List<String>> partition(String s) { // System.out.println(isHuiWenChuan("")); List<List<String>> result = new ArrayList<>(); backroll(result,s,new ArrayList<>()); return result; } void backroll(List<List<String>> result,String s,List<String> templist){ //每次判断[0,i]是否是回文串,然后对剩下[i,s.szie()-1]递归 if(s.length() == 0){ //s被分割变成[i,s.szie()-1] result.add(new ArrayList<>(templist)); return; } for(int i = 1;i <= s.length();i++){ String temp = s.substring(0,i); if(isHuiWenChuan(temp)){ templist.add(temp); backroll(result,s.substring(i),templist);//substring(i)是截取[i,length-1]的部分 templist.remove(templist.size()-1); } } } boolean isHuiWenChuan(String temp){ if(temp == null) return true; int left = 0,right = temp.length()-1; while(left <= right){ if(temp.charAt(left) != temp.charAt(right)){ return false; } left++; right--; } return true; } } //动态规划优化————这下回溯模板又可以套上了(start又回来啦)。 class Solution { public List<List<String>> partition(String s) { // System.out.println(isHuiWenChuan("")); List<List<String>> result = new ArrayList<>(); //动态规划 int len = s.length(); int[][] dp = new int[len][len]; for(int right = 0;right < len;right++){ for(int left = 0;left <= right;left++){ if(s.charAt(left) == s.charAt(right) && (right - left <= 2 || dp[left+1][right-1] == 1)){//right - left <= 2表示一个字符时必定是回文串 dp[left][right] = 1; } } } // for(int i = 0;i < len;i++){ // for(int j = 0;j < len;j++){ // System.out.print(dp[i][j]+" "); // } // System.out.println(); // } backroll(0,result,s,new ArrayList<>(),dp); return result; } void backroll(int start,List<List<String>> result,String s,List<String> templist,int[][] dp){ if(start == s.length()){ //s被分割变成[i,s.szie()-1] result.add(new ArrayList<>(templist)); return; } for(int i = start;i < s.length();i++){ if(dp[start][i] == 1){ // System.out.println("start="+start+" i+1="+(i+1)+" sub="+s.substring(start,i+1)); templist.add(s.substring(start,i+1)); backroll(i+1,result,s,templist,dp);//substring(i)是截取[i,length-1]的部分 templist.remove(templist.size()-1); } } } } -
337. 打家劫舍 III
难度中等796收藏分享切换为英文接收动态反馈
在上次打劫完一条街道之后和一圈房屋后,小偷又发现了一个新的可行窃的地区。这个地区只有一个入口,我们称之为“根”。 除了“根”之外,每栋房子有且只有一个“父“房子与之相连。一番侦察之后,聪明的小偷意识到“这个地方的所有房屋的排列类似于一棵二叉树”。 如果两个直接相连的房子在同一天晚上被打劫,房屋将自动报警。
计算在不触动警报的情况下,小偷一晚能够盗取的最高金额。
示例 1:
输入: [3,2,3,null,3,null,1] 3 / \ 2 3 \ \ 3 1 输出: 7 解释: 小偷一晚能够盗取的最高金额 = 3 + 3 + 1 = 7.示例 2:
输入: [3,4,5,1,3,null,1] 3 / \ 4 5 / \ \ 1 3 1 输出: 9 解释: 小偷一晚能够盗取的最高金额 = 4 + 5 = 9.//刚开始的一个错误想法。 class Solution { int jishusum = 0; int oushusum = 0; public int rob(TreeNode root) { //遍历二叉树,记录层数,当层数是奇数时维护一个总和;偶数时维护一个总和。比较两个总和,输出较高者。--行不通,因为可以隔2层然后相加。所以要求每一层同下面隔至少1层的总和。状态数组该如何表示?。。。 backroll(root,0); return Math.max(jishusum,oushusum); } public void backroll(TreeNode root,int num){//num表示当前层数序号 if(root == null){ return; } if(num % 2 == 0){ oushusum+=root.val; } else{ jishusum+=root.val; } num++; backroll(root.left,num); backroll(root.right,num); } }后来看了官方题解,动态规划不一定要数组,也可以是哈希表:
/** * Definition for a binary tree node. * public class TreeNode { * int val; * TreeNode left; * TreeNode right; * TreeNode() {} * TreeNode(int val) { this.val = val; } * TreeNode(int val, TreeNode left, TreeNode right) { * this.val = val;9 * this.left = left; * this.right = right; * } * } */ class Solution { HashMap<TreeNode,Integer> f = new HashMap<>(); HashMap<TreeNode,Integer> g = new HashMap<>(); public int rob(TreeNode root) { //动态规划,f(root)表示选取当前节点root时树的最大金额;g(root)表示不选取当前节点时树的最大金额。 backroll(root); return Math.max(f.getOrDefault(root,0),g.getOrDefault(root,0)); } public void backroll(TreeNode root){ if(root == null){ return; } backroll(root.left); backroll(root.right); f.put(root,root.val+g.getOrDefault(root.left,0)+g.getOrDefault(root.right,0)); g.put(root,Math.max(f.getOrDefault(root.left,0),g.getOrDefault(root.left,0))+Math.max(g.getOrDefault(root.right,0),f.getOrDefault(root.right,0))); } } -
647. 回文子串
难度中等
给定一个字符串,你的任务是计算这个字符串中有多少个回文子串。
具有不同开始位置或结束位置的子串,即使是由相同的字符组成,也会被视作不同的子串。
示例 1:
输入:"abc" 输出:3 解释:三个回文子串: "a", "b", "c"示例 2:
输入:"aaa" 输出:6 解释:6个回文子串: "a", "a", "a", "aa", "aa", "aaa"提示:
- 输入的字符串长度不会超过 1000 。
class Solution { public int countSubstrings(String s) { //dp[i][j]表示s[i,j]是否回文串 int answer = 0; int length = s.length(); boolean[][] dp = new boolean[length][length]; for(int j = 0;j < length;j++){ for(int i = 0;i <= j;i++){ if(s.charAt(i) == s.charAt(j) && (j - i < 2 || dp[i+1][j-1])){ dp[i][j] = true; answer++; } } } return answer; } } -
64. 最小路径和
难度中等
给定一个包含非负整数的
*m* x *n*网格grid,请找出一条从左上角到右下角的路径,使得路径上的数字总和为最小。说明:每次只能向下或者向右移动一步。
示例 1:

输入:grid = [[1,3,1],[1,5,1],[4,2,1]] 输出:7 解释:因为路径 1→3→1→1→1 的总和最小。示例 2:
输入:grid = [[1,2,3],[4,5,6]] 输出:12提示:
m == grid.lengthn == grid[i].length1 <= m, n <= 2000 <= grid[i][j] <= 100
class Solution { public int minPathSum(int[][] grid) { //dp[i][j]表示网格[0,i][0,j]的总和最小值 int row = grid.length; int col = grid[0].length; int[][] dp = new int[row][col]; for(int i = 0;i < row;i++){ for(int j = 0;j < col;j++){ if(i-1 < 0 && j-1 < 0){ dp[i][j] = grid[i][j]; } else if(i-1 < 0){ dp[i][j] = dp[i][j-1] + grid[i][j]; } else if(j-1 < 0){ dp[i][j] = dp[i-1][j] + grid[i][j]; } else{ dp[i][j] = Math.min(dp[i-1][j],dp[i][j-1]) + grid[i][j]; } } } return dp[row-1][col-1]; } } -
309. 最佳买卖股票时机含冷冻期
难度中等
给定一个整数数组,其中第 i 个元素代表了第 i 天的股票价格 。
设计一个算法计算出最大利润。在满足以下约束条件下,你可以尽可能地完成更多的交易(多次买卖一支股票):
- 你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
- 卖出股票后,你无法在第二天买入股票 (即冷冻期为 1 天)。
示例:
输入: [1,2,3,0,2] 输出: 3 解释: 对应的交易状态为: [买入, 卖出, 冷冻期, 买入, 卖出]初看题目这状态转移方程好难列呀。。。今天的利润是取决于
- 你今天卖还是不卖;
- 昨天的最佳状态。
而昨天的最佳状态有三种——持有,刚卖(今天冷冻期),卖了很久(今天不是冷冻期)。你今天的最大利润就是昨天的最佳状态+对应昨天状态下今天的卖还是不卖还是买入。(买入/不卖不一定比卖利润少)
三种状态转移方程:(最难的部分)
f[i][0]:到了今天持有股票,于是取以下的最大利润:昨天持有今天卖出、昨天卖出今天冷冻期、昨天早已卖出今天买入、
目前我知道的动态规划有这几种表现形式:dp[i][j](表示i~j区间的某个推导状态,或者[0,i],[0,j]两个区的比较状态)跟f(i)(表示第i天/格的推导状态),dp[i][0]与dp[i][1](分别表示两种状态的第i天/格的推导状态,还可以第三种状态、第四种......),甚至还有哈希表只为记录键值对的。
-
466. 统计重复个数
难度困难
由 n 个连接的字符串 s 组成字符串 S,记作
S = [s,n]。例如,["abc",3]=“abcabcabc”。如果我们可以从 s2 中删除某些字符使其变为 s1,则称字符串 s1 可以从字符串 s2 获得。例如,根据定义,"abc" 可以从 “abdbec” 获得,但不能从 “acbbe” 获得。
现在给你两个非空字符串 s1 和 s2(每个最多 100 个字符长)和两个整数 0 ≤ n1 ≤ 10^6 和 1 ≤ n2 ≤ 10^6。现在考虑字符串 S1 和 S2,其中
S1=[s1,n1]、S2=[s2,n2]。请你找出一个可以满足使
[S2,M]从S1获得的最大整数 M 。示例:
输入: s1 ="acb",n1 = 4 s2 ="ab",n2 = 2 返回: 2一看到题目“两个整数 0 ≤ n1 ≤ 10^6 和 1 ≤ n2 ≤ 10^6”我就知道不能用暴力解,果然卡在第12个例子,n1已经开始是10万起步了:
class Solution { public int getMaxRepetitions(String s1, int n1, String s2, int n2) { // //组成要测试的真实字符串 String shuru1 = new String(); String shuru2 = new String(); for(int i = 0;i < n1;i++){ shuru1 += s1; } for(int j = 0;j < n2;j++){ shuru2 += s2; } int len1 = shuru1.length(); int len2 = shuru2.length(); int i = 0; int M = 0; for(int j = 0;j < len2 && i < len1;i++){ if(shuru1.charAt(i) == shuru2.charAt(j)){ j++; } if(j == len2){ M+=1; j = 0; } } return M; } }显示超限:
12 / 49 个通过测试用例 状态:超出时间限制 最后执行的输入: "lovelive" 100000 "lovelive" 100000状态转移方程难想的一批。。。
每日一题
-
1006. 笨阶乘
栈,逆波兰表达式
难度中等
通常,正整数
n的阶乘是所有小于或等于n的正整数的乘积。例如,factorial(10) = 10 * 9 * 8 * 7 * 6 * 5 * 4 * 3 * 2 * 1。相反,我们设计了一个笨阶乘
clumsy:在整数的递减序列中,我们以一个固定顺序的操作符序列来依次替换原有的乘法操作符:乘法(*),除法(/),加法(+)和减法(-)。例如,
clumsy(10) = 10 * 9 / 8 + 7 - 6 * 5 / 4 + 3 - 2 * 1。然而,这些运算仍然使用通常的算术运算顺序:我们在任何加、减步骤之前执行所有的乘法和除法步骤,并且按从左到右处理乘法和除法步骤。另外,我们使用的除法是地板除法(floor division),所以
10 * 9 / 8等于11。这保证结果是一个整数。实现上面定义的笨函数:给定一个整数
N,它返回N的笨阶乘。示例 1:
输入:4 输出:7 解释:7 = 4 * 3 / 2 + 1示例 2:
输入:10 输出:12 解释:12 = 10 * 9 / 8 + 7 - 6 * 5 / 4 + 3 - 2 * 1提示:
1 <= N <= 10000-2^31 <= answer <= 2^31 - 1(答案保证符合 32 位整数。)
//看了官方题解默出来的O(N)时间空间复杂度 class Solution { public int clumsy(int N) { Stack<Integer> stack = new Stack<>(); stack.push(N); N--; int index = 0;//对当前的运算符进行计数 //遍历N到1,遇到乘除就先处理,加减就入栈。 while(N > 0){ if(index % 4 == 0){ stack.push(stack.pop() * N); } if(index % 4 == 1){ stack.push(stack.pop() / N); } if(index % 4 == 2){ stack.push(N); } if(index % 4 == 3){ stack.push(-N); } index++; N--; } //对栈内容进行相加 int sum = 0; while(!stack.empty()){ sum += stack.pop(); } return sum; } } -
面试题 17.21. 直方图的水量
动态规划
难度困难
给定一个直方图(也称柱状图),假设有人从上面源源不断地倒水,最后直方图能存多少水量?直方图的宽度为 1。

上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的直方图,在这种情况下,可以接 6 个单位的水(蓝色部分表示水)。 感谢 Marcos 贡献此图。
示例:
输入: [0,1,0,2,1,0,1,3,2,1,2,1] 输出: 6//看了官方思路 class Solution { public int trap(int[] height) { //动态规划 int n = height.length; if(n ==0) return 0; int[] leftmax = new int[n];//记录i左边的最大高度 int[] rightmax = new int[n]; leftmax[0] = height[0]; rightmax[n-1] = height[n-1]; for(int i = 1;i < height.length;i++){ leftmax[i] = leftmax[i-1] > height[i] ? leftmax[i-1] : height[i]; } for(int i = n-2;i >= 0;i--){ rightmax[i] = rightmax[i+1] > height[i] ? rightmax[i+1] : height[i]; } int sum = 0; for(int i = 0;i < n;i++){ sum += (Math.min(leftmax[i],rightmax[i]) - height[i]); } return sum; } } -
1143. 最长公共子序列
难度中等
给定两个字符串
text1和text2,返回这两个字符串的最长 公共子序列 的长度。如果不存在 公共子序列 ,返回0。一个字符串的 子序列 是指这样一个新的字符串:它是由原字符串在不改变字符的相对顺序的情况下删除某些字符(也可以不删除任何字符)后组成的新字符串。
- 例如,
"ace"是"abcde"的子序列,但"aec"不是"abcde"的子序列。
两个字符串的 公共子序列 是这两个字符串所共同拥有的子序列。
示例 1:
输入:text1 = "abcde", text2 = "ace" 输出:3 解释:最长公共子序列是 "ace" ,它的长度为 3 。示例 2:
输入:text1 = "abc", text2 = "abc" 输出:3 解释:最长公共子序列是 "abc" ,它的长度为 3 。示例 3:
输入:text1 = "abc", text2 = "def" 输出:0 解释:两个字符串没有公共子序列,返回 0 。提示:
1 <= text1.length, text2.length <= 1000text1和text2仅由小写英文字符组成。
下面的题解为什么不用dp[i][j]表示第一个字符串的[0,i]和第二个字符串的[0,j]是因为可以省去特殊考虑初始化状态dp[0][0],整合到循环里。
//大佬题解照搬 class Solution { public int longestCommonSubsequence(String text1, String text2) { int n1 = text1.length(),n2 = text2.length(); int[][] dp = new int[n1+1][n2+1];//dp[i][j]表示text1的[0,i-1]和text2的[0,j-1]的最长公共子序列长度 for(int i = 1;i <= n1;i++){ for(int j = 1;j <= n2;j++){ if(text1.charAt(i-1) == text2.charAt(j-1)){//要么更新状态 dp[i][j] = dp[i-1][j-1] +1; } else{//要么从上一个状态继承不变 dp[i][j] = Math.max(dp[i-1][j],dp[i][j-1]); } } } return dp[n1][n2]; } } - 例如,
-
461. 汉明距离
难度简单
两个整数之间的汉明距离指的是这两个数字对应二进制位不同的位置的数目。
给出两个整数
x和y,计算它们之间的汉明距离。注意:
0 ≤x,y< 231.示例:
输入: x = 1, y = 4 输出: 2 解释: 1 (0 0 0 1) 4 (0 1 0 0) ↑ ↑ 上面的箭头指出了对应二进制位不同的位置。这里偷了懒,用了Integer.toBinaryString()方法将十进制化成二进制。实际要自己转化可以用%2得到当前的二进制数,然后/2,循环:
public void binaryToDecimal(int n){ int t = 0; //用来记录位数 int bin = 0; //用来记录最后的二进制数 int r = 0; //用来存储余数 while(n != 0){ r = n % 2; n = n / 2; bin += r * Math().pow(10,t); t++; } System.out.println(bin); }class Solution { public int hammingDistance(int x, int y) { String strx = Integer.toBinaryString(x); String stry = Integer.toBinaryString(y); int xlen = strx.length(),ylen = stry.length(); //给字符串补足0 int bigger = xlen < ylen ? ylen : xlen; if(bigger == xlen){//stry比较小,需要补足0 for(int i = 0,j = bigger - ylen; i < j;i++){ stry = "0" + stry; } } else{ for(int i = 0,j = bigger - xlen; i < j;i++){ strx = "0" + strx; } } int sum = 0; for(int i = 0;i < bigger;i++){ if(strx.charAt(i) != stry.charAt(i)){ sum += 1; } } // System.out.println(strx+" | "+stry); return sum; } } -
781. 森林中的兔子
难度中等
森林中,每个兔子都有颜色。其中一些兔子(可能是全部)告诉你还有多少其他的兔子和自己有相同的颜色。我们将这些回答放在
answers数组里。返回森林中兔子的最少数量。
示例: 输入: answers = [1, 1, 2] 输出: 5 解释: 两只回答了 "1" 的兔子可能有相同的颜色,设为红色。 之后回答了 "2" 的兔子不会是红色,否则他们的回答会相互矛盾。 设回答了 "2" 的兔子为蓝色。 此外,森林中还应有另外 2 只蓝色兔子的回答没有包含在数组中。 因此森林中兔子的最少数量是 5: 3 只回答的和 2 只没有回答的。 输入: answers = [10, 10, 10] 输出: 11 输入: answers = [] 输出: 0说明:
answers的长度最大为1000。answers[i]是在[0, 999]范围内的整数。
题意可知,相同颜色的兔子一定会说一样的数字;说一样数字的兔子却不一定是相同颜色的。
为了求得兔子的最少数量,需要尽可能的将说同一个数字的兔子归为相同颜色,当说相同数字的兔子数量已经超过了所说的数字+1(这个1是指说数字的兔子本身)时,就要被迫将兔子总数+这个数字。
题解里说到要用到贪心,但是我还没学贪心。。。也不知道为什么这样就用到了贪心。
//看了题解宫水三叶大佬的思路写的 class Solution { public int numRabbits(int[] answers) { Arrays.sort(answers);//排序是为了更好的将相同颜色的兔子覆盖 int n = answers.length; int ans = 0; for(int i = 0;i < n;i++){ ans += answers[i] + 1; int k = answers[i]; while(k-- > 0 && i+1 < n && answers[i] == answers[i+1]){ i++; } } return ans; } } -
88. 合并两个有序数组
难度简单
给你两个有序整数数组
nums1和nums2,请你将nums2合并到nums1中,使nums1成为一个有序数组。初始化
nums1和nums2的元素数量分别为m和n。你可以假设nums1的空间大小等于m + n,这样它就有足够的空间保存来自nums2的元素。示例 1:
输入:nums1 = [1,2,3,0,0,0], m = 3, nums2 = [2,5,6], n = 3 输出:[1,2,2,3,5,6]示例 2:
输入:nums1 = [1], m = 1, nums2 = [], n = 0 输出:[1]提示:
nums1.length == m + nnums2.length == n0 <= m, n <= 2001 <= m + n <= 200-109 <= nums1[i], nums2[i] <= 109
class Solution { public void merge(int[] nums1, int m, int[] nums2, int n) { for(int i = m,j = 0;i < m+n && j < n;i++,j++){ nums1[i] = nums2[j]; } Arrays.sort(nums1); } } -
80. 删除有序数组中的重复项 II
难度中等404收藏分享切换为英文接收动态反馈
给你一个有序数组
nums,请你 原地 删除重复出现的元素,使每个元素 最多出现两次 ,返回删除后数组的新长度。不要使用额外的数组空间,你必须在 原地 修改输入数组 并在使用 O(1) 额外空间的条件下完成。
说明:
为什么返回数值是整数,但输出的答案是数组呢?
请注意,输入数组是以「引用」方式传递的,这意味着在函数里修改输入数组对于调用者是可见的。
你可以想象内部操作如下:
// nums 是以“引用”方式传递的。也就是说,不对实参做任何拷贝 int len = removeDuplicates(nums); // 在函数里修改输入数组对于调用者是可见的。 // 根据你的函数返回的长度, 它会打印出数组中 该长度范围内 的所有元素。 for (int i = 0; i < len; i++) { print(nums[i]); }示例 1:
输入:nums = [1,1,1,2,2,3] 输出:5, nums = [1,1,2,2,3] 解释:函数应返回新长度 length = 5, 并且原数组的前五个元素被修改为 1, 1, 2, 2, 3 。 不需要考虑数组中超出新长度后面的元素。示例 2:
输入:nums = [0,0,1,1,1,1,2,3,3] 输出:7, nums = [0,0,1,1,2,3,3] 解释:函数应返回新长度 length = 7, 并且原数组的前五个元素被修改为 0, 0, 1, 1, 2, 3, 3 。 不需要考虑数组中超出新长度后面的元素。提示:
0 <= nums.length <= 3 * 104-104 <= nums[i] <= 104nums已按升序排列
//暴力解法 class Solution { public int removeDuplicates(int[] nums) { //暴力 int num = 0; int k = 0;//由于nums已经排序,k记录当前字母出现次数 for(int i = 0,j = nums.length;i < j-1;i++){ if(nums[i] == nums[i+1]){ k++; } else{ k = 0; } if(k >= 2){ //此处应该移除此元素 } } } } //双指针 class Solution { public int removeDuplicates(int[] nums) { int fast = 2,slow = 2;//nums的[0,slow-1]表示答案数组;[slow,fast]表示正在判断的范围,slow是拿来判断要不要覆盖的,fast是哨兵。 int n = nums.length; while(fast < n){ if(nums[slow-2] != nums[fast]){//遇到间隔2个不同的就覆盖,当遇到相同的时候slow将不增加 nums[slow] = nums[fast]; slow++; } fast++; } return slow; } } -
81. 搜索旋转排序数组 II
难度中等
已知存在一个按非降序排列的整数数组
nums,数组中的值不必互不相同。在传递给函数之前,
nums在预先未知的某个下标k(0 <= k < nums.length)上进行了 旋转 ,使数组变为[nums[k], nums[k+1], ..., nums[n-1], nums[0], nums[1], ..., nums[k-1]](下标 从 0 开始 计数)。例如,[0,1,2,4,4,4,5,6,6,7]在下标5处经旋转后可能变为[4,5,6,6,7,0,1,2,4,4]。给你 旋转后 的数组
nums和一个整数target,请你编写一个函数来判断给定的目标值是否存在于数组中。如果nums中存在这个目标值target,则返回true,否则返回false。示例 1:
输入:nums = [2,5,6,0,0,1,2], target = 0 输出:true示例 2:
输入:nums = [2,5,6,0,0,1,2], target = 3 输出:false提示:
1 <= nums.length <= 5000-104 <= nums[i] <= 104- 题目数据保证
nums在预先未知的某个下标上进行了旋转 -104 <= target <= 104
进阶:
- 这是 搜索旋转排序数组 的延伸题目,本题中的
nums可能包含重复元素。 - 这会影响到程序的时间复杂度吗?会有怎样的影响,为什么?
//逃课大法 class Solution { public boolean search(int[] nums, int target) { List<Integer> result = Arrays.stream(nums).boxed().collect(Collectors.toList()); return result.contains(target); } } //正经题解 //直接排序然后二分,或者直接遍历查找。 -
153. 寻找旋转排序数组中的最小值
难度中等
已知一个长度为
n的数组,预先按照升序排列,经由1到n次 旋转 后,得到输入数组。例如,原数组nums = [0,1,2,4,5,6,7]在变化后可能得到:- 若旋转
4次,则可以得到[4,5,6,7,0,1,2] - 若旋转
7次,则可以得到[0,1,2,4,5,6,7]
注意,数组
[a[0], a[1], a[2], ..., a[n-1]]旋转一次 的结果为数组[a[n-1], a[0], a[1], a[2], ..., a[n-2]]。给你一个元素值 互不相同 的数组
nums,它原来是一个升序排列的数组,并按上述情形进行了多次旋转。请你找出并返回数组中的 最小元素 。示例 1:
输入:nums = [3,4,5,1,2] 输出:1 解释:原数组为 [1,2,3,4,5] ,旋转 3 次得到输入数组。示例 2:
输入:nums = [4,5,6,7,0,1,2] 输出:0 解释:原数组为 [0,1,2,4,5,6,7] ,旋转 4 次得到输入数组。示例 3:
输入:nums = [11,13,15,17] 输出:11 解释:原数组为 [11,13,15,17] ,旋转 4 次得到输入数组。提示:
n == nums.length1 <= n <= 5000-5000 <= nums[i] <= 5000nums中的所有整数 互不相同nums原来是一个升序排序的数组,并进行了1至n次旋转
我第一反应是:
class Solution { public int findMin(int[] nums) { Arrays.sort(nums); return nums[0]; } }然后正经看了题解:
class Solution { public int findMin(int[] nums) { //二分法,不过判断二分的条件不是中间值大于/小于目标值,而是中间值大于/小于右边界。因为旋转数组的最小值左半部分一定全部大于右半部分,当中间下标值大于右边界值时说明可以左半部分可以舍弃,当中间下标值小于右边界值时说明右半部分可以舍弃。 int left = 0; int right = nums.length - 1; while(left < right){ int pivot = (left+right)/2; if(nums[pivot] < nums[right]){ right = pivot; //缩小右边界 } else { left = pivot +1; //缩小左边界,并直接让左边界前进一位,以便作为结果返回(当left==right时会结束循环) } } return nums[left]; } } - 若旋转
-
154. 寻找旋转排序数组中的最小值 II
难度困难
已知一个长度为
n的数组,预先按照升序排列,经由1到n次 旋转 后,得到输入数组。例如,原数组nums = [0,1,4,4,5,6,7]在变化后可能得到:- 若旋转
4次,则可以得到[4,5,6,7,0,1,4] - 若旋转
7次,则可以得到[0,1,4,4,5,6,7]
注意,数组
[a[0], a[1], a[2], ..., a[n-1]]旋转一次 的结果为数组[a[n-1], a[0], a[1], a[2], ..., a[n-2]]。给你一个可能存在 重复 元素值的数组
nums,它原来是一个升序排列的数组,并按上述情形进行了多次旋转。请你找出并返回数组中的 最小元素 。示例 1:
输入:nums = [1,3,5] 输出:1示例 2:
输入:nums = [2,2,2,0,1] 输出:0提示:
n == nums.length1 <= n <= 5000-5000 <= nums[i] <= 5000nums原来是一个升序排序的数组,并进行了1至n次旋转
进阶:
- 这道题是 寻找旋转排序数组中的最小值 的延伸题目。
- 允许重复会影响算法的时间复杂度吗?会如何影响,为什么?
//第一反应还是直接sort再return nums[0],也能过。 class Solution { public int findMin(int[] nums) { //二分法,只不过比较的不是目标值,而是右边界 int left = 0,right = nums.length-1; while(left < right){ int pivot = (left + right)/2; if(nums[pivot] < nums[right]){ right = pivot; } else if(nums[pivot] > nums[right]){ left = pivot + 1; } else{ right -= 1; } } return nums[left]; } }这个图是精髓:
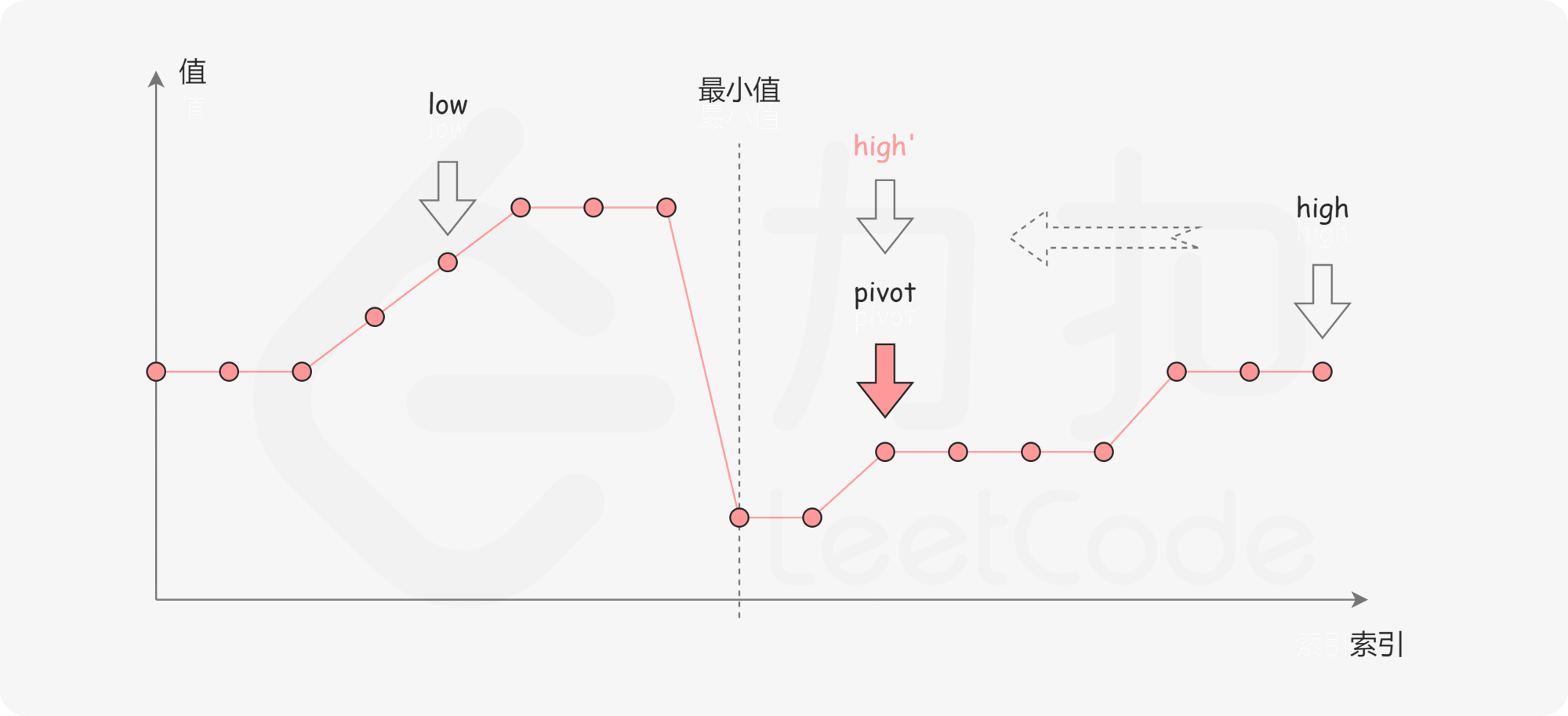
- 若旋转
-
263. 丑数
难度简单
给你一个整数
n,请你判断n是否为 丑数 。如果是,返回true;否则,返回false。丑数 就是只包含质因数
2、3和/或5的正整数。示例 1:
输入:n = 6 输出:true 解释:6 = 2 × 3示例 2:
输入:n = 8 输出:true 解释:8 = 2 × 2 × 2示例 3:
输入:n = 14 输出:false 解释:14 不是丑数,因为它包含了另外一个质因数 7 。示例 4:
输入:n = 1 输出:true 解释:1 通常被视为丑数。提示:
-231 <= n <= 231 - 1
class Solution { public boolean isUgly(int n) { // 没什么套路,就是数学分析,负数和0不是丑数,1是丑数;如果不能被2,3,5一直除到不能除为止,如果最后的余数不为1就不是丑数。 if(n <= 0){ return false; } while(n % 2 == 0){ n /= 2; } while(n % 3 == 0){ n /= 3; } while(n % 5 == 0){ n /= 5; } return n == 1; } } -
264. 丑数 II
难度中等554收藏分享切换为英文接收动态反馈
给你一个整数
n,请你找出并返回第n个 丑数 。丑数 就是只包含质因数
2、3和/或5的正整数。示例 1:
输入:n = 10 输出:12 解释:[1, 2, 3, 4, 5, 6, 8, 9, 10, 12] 是由前 10 个丑数组成的序列。示例 2:
输入:n = 1 输出:1 解释:1 通常被视为丑数。提示:
1 <= n <= 1690
//面向测试用例编程 class Solution { public int nthUglyNumber(int n) { int all[] = {1,2,3,4,5,6,8,9,10,12,15,16,18,20,24,25,27,30,32,36,40,45,48,50,54,60,64,72,75,80,81,90,96,100,108,120,125,128,135,144,150,160,162,180,192,200,216,225,240,243,250,256,270,288,300,320,324,360,375,384,400,405,432,450,480,486,500,512,540,576,600,625,640,648,675,720,729,750,768,800,810,864,900,960,972,1000,1024,1080,1125,1152,1200,1215,1250,1280,1296,1350,1440,1458,1500,1536,1600,1620,1728,1800,1875,1920,1944,2000,2025,2048,2160,2187,2250,2304,2400,2430,2500,2560,2592,2700,2880,2916,3000,3072,3125,3200,3240,3375,3456,3600,3645,3750,3840,3888,4000,4050,4096,4320,4374,4500,4608,4800,4860,5000,5120,5184,5400,5625,5760,5832,6000,6075,6144,6250,6400,6480,6561,6750,6912,7200,7290,7500,7680,7776,8000,8100,8192,8640,8748,9000,9216,9375,9600,9720,10000,10125,10240,10368,10800,10935,11250,11520,11664,12000,12150,12288,12500,12800,12960,13122,13500,13824,14400,14580,15000,15360,15552,15625,16000,16200,16384,16875,17280,17496,18000,18225,18432,18750,19200,19440,19683,20000,20250,20480,20736,21600,21870,22500,23040,23328,24000,24300,24576,25000,25600,25920,26244,27000,27648,28125,28800,29160,30000,30375,30720,31104,31250,32000,32400,32768,32805,33750,34560,34992,36000,36450,36864,37500,38400,38880,39366,40000,40500,40960,41472,43200,43740,45000,46080,46656,46875,48000,48600,49152,50000,50625,51200,51840,52488,54000,54675,55296,56250,57600,58320,59049,60000,60750,61440,62208,62500,64000,64800,65536,65610,67500,69120,69984,72000,72900,73728,75000,76800,77760,78125,78732,80000,81000,81920,82944,84375,86400,87480,90000,91125,92160,93312,93750,96000,97200,98304,98415,100000,101250,102400,103680,104976,108000,109350,110592,112500,115200,116640,118098,120000,121500,122880,124416,125000,128000,129600,131072,131220,135000,138240,139968,140625,144000,145800,147456,150000,151875,153600,155520,156250,157464,160000,162000,163840,164025,165888,168750,172800,174960,177147,180000,182250,184320,186624,187500,192000,194400,196608,196830,200000,202500,204800,207360,209952,216000,218700,221184,225000,230400,233280,234375,236196,240000,243000,245760,248832,250000,253125,256000,259200,262144,262440,270000,273375,276480,279936,281250,288000,291600,294912,295245,300000,303750,307200,311040,312500,314928,320000,324000,327680,328050,331776,337500,345600,349920,354294,360000,364500,368640,373248,375000,384000,388800,390625,393216,393660,400000,405000,409600,414720,419904,421875,432000,437400,442368,450000,455625,460800,466560,468750,472392,480000,486000,491520,492075,497664,500000,506250,512000,518400,524288,524880,531441,540000,546750,552960,559872,562500,576000,583200,589824,590490,600000,607500,614400,622080,625000,629856,640000,648000,655360,656100,663552,675000,691200,699840,703125,708588,720000,729000,737280,746496,750000,759375,768000,777600,781250,786432,787320,800000,810000,819200,820125,829440,839808,843750,864000,874800,884736,885735,900000,911250,921600,933120,937500,944784,960000,972000,983040,984150,995328,1000000,1012500,1024000,1036800,1048576,1049760,1062882,1080000,1093500,1105920,1119744,1125000,1152000,1166400,1171875,1179648,1180980,1200000,1215000,1228800,1244160,1250000,1259712,1265625,1280000,1296000,1310720,1312200,1327104,1350000,1366875,1382400,1399680,1406250,1417176,1440000,1458000,1474560,1476225,1492992,1500000,1518750,1536000,1555200,1562500,1572864,1574640,1594323,1600000,1620000,1638400,1640250,1658880,1679616,1687500,1728000,1749600,1769472,1771470,1800000,1822500,1843200,1866240,1875000,1889568,1920000,1944000,1953125,1966080,1968300,1990656,2000000,2025000,2048000,2073600,2097152,2099520,2109375,2125764,2160000,2187000,2211840,2239488,2250000,2278125,2304000,2332800,2343750,2359296,2361960,2400000,2430000,2457600,2460375,2488320,2500000,2519424,2531250,2560000,2592000,2621440,2624400,2654208,2657205,2700000,2733750,2764800,2799360,2812500,2834352,2880000,2916000,2949120,2952450,2985984,3000000,3037500,3072000,3110400,3125000,3145728,3149280,3188646,3200000,3240000,3276800,3280500,3317760,3359232,3375000,3456000,3499200,3515625,3538944,3542940,3600000,3645000,3686400,3732480,3750000,3779136,3796875,3840000,3888000,3906250,3932160,3936600,3981312,4000000,4050000,4096000,4100625,4147200,4194304,4199040,4218750,4251528,4320000,4374000,4423680,4428675,4478976,4500000,4556250,4608000,4665600,4687500,4718592,4723920,4782969,4800000,4860000,4915200,4920750,4976640,5000000,5038848,5062500,5120000,5184000,5242880,5248800,5308416,5314410,5400000,5467500,5529600,5598720,5625000,5668704,5760000,5832000,5859375,5898240,5904900,5971968,6000000,6075000,6144000,6220800,6250000,6291456,6298560,6328125,6377292,6400000,6480000,6553600,6561000,6635520,6718464,6750000,6834375,6912000,6998400,7031250,7077888,7085880,7200000,7290000,7372800,7381125,7464960,7500000,7558272,7593750,7680000,7776000,7812500,7864320,7873200,7962624,7971615,8000000,8100000,8192000,8201250,8294400,8388608,8398080,8437500,8503056,8640000,8748000,8847360,8857350,8957952,9000000,9112500,9216000,9331200,9375000,9437184,9447840,9565938,9600000,9720000,9765625,9830400,9841500,9953280,10000000,10077696,10125000,10240000,10368000,10485760,10497600,10546875,10616832,10628820,10800000,10935000,11059200,11197440,11250000,11337408,11390625,11520000,11664000,11718750,11796480,11809800,11943936,12000000,12150000,12288000,12301875,12441600,12500000,12582912,12597120,12656250,12754584,12800000,12960000,13107200,13122000,13271040,13286025,13436928,13500000,13668750,13824000,13996800,14062500,14155776,14171760,14348907,14400000,14580000,14745600,14762250,14929920,15000000,15116544,15187500,15360000,15552000,15625000,15728640,15746400,15925248,15943230,16000000,16200000,16384000,16402500,16588800,16777216,16796160,16875000,17006112,17280000,17496000,17578125,17694720,17714700,17915904,18000000,18225000,18432000,18662400,18750000,18874368,18895680,18984375,19131876,19200000,19440000,19531250,19660800,19683000,19906560,20000000,20155392,20250000,20480000,20503125,20736000,20971520,20995200,21093750,21233664,21257640,21600000,21870000,22118400,22143375,22394880,22500000,22674816,22781250,23040000,23328000,23437500,23592960,23619600,23887872,23914845,24000000,24300000,24576000,24603750,24883200,25000000,25165824,25194240,25312500,25509168,25600000,25920000,26214400,26244000,26542080,26572050,26873856,27000000,27337500,27648000,27993600,28125000,28311552,28343520,28697814,28800000,29160000,29296875,29491200,29524500,29859840,30000000,30233088,30375000,30720000,31104000,31250000,31457280,31492800,31640625,31850496,31886460,32000000,32400000,32768000,32805000,33177600,33554432,33592320,33750000,34012224,34171875,34560000,34992000,35156250,35389440,35429400,35831808,36000000,36450000,36864000,36905625,37324800,37500000,37748736,37791360,37968750,38263752,38400000,38880000,39062500,39321600,39366000,39813120,39858075,40000000,40310784,40500000,40960000,41006250,41472000,41943040,41990400,42187500,42467328,42515280,43046721,43200000,43740000,44236800,44286750,44789760,45000000,45349632,45562500,46080000,46656000,46875000,47185920,47239200,47775744,47829690,48000000,48600000,48828125,49152000,49207500,49766400,50000000,50331648,50388480,50625000,51018336,51200000,51840000,52428800,52488000,52734375,53084160,53144100,53747712,54000000,54675000,55296000,55987200,56250000,56623104,56687040,56953125,57395628,57600000,58320000,58593750,58982400,59049000,59719680,60000000,60466176,60750000,61440000,61509375,62208000,62500000,62914560,62985600,63281250,63700992,63772920,64000000,64800000,65536000,65610000,66355200,66430125,67108864,67184640,67500000,68024448,68343750,69120000,69984000,70312500,70778880,70858800,71663616,71744535,72000000,72900000,73728000,73811250,74649600,75000000,75497472,75582720,75937500,76527504,76800000,77760000,78125000,78643200,78732000,79626240,79716150,80000000,80621568,81000000,81920000,82012500,82944000,83886080,83980800,84375000,84934656,85030560,86093442,86400000,87480000,87890625,88473600,88573500,89579520,90000000,90699264,91125000,92160000,93312000,93750000,94371840,94478400,94921875,95551488,95659380,96000000,97200000,97656250,98304000,98415000,99532800,100000000,100663296,100776960,101250000,102036672,102400000,102515625,103680000,104857600,104976000,105468750,106168320,106288200,107495424,108000000,109350000,110592000,110716875,111974400,112500000,113246208,113374080,113906250,114791256,115200000,116640000,117187500,117964800,118098000,119439360,119574225,120000000,120932352,121500000,122880000,123018750,124416000,125000000,125829120,125971200,126562500,127401984,127545840,128000000,129140163,129600000,131072000,131220000,132710400,132860250,134217728,134369280,135000000,136048896,136687500,138240000,139968000,140625000,141557760,141717600,143327232,143489070,144000000,145800000,146484375,147456000,147622500,149299200,150000000,150994944,151165440,151875000,153055008,153600000,155520000,156250000,157286400,157464000,158203125,159252480,159432300,160000000,161243136,162000000,163840000,164025000,165888000,167772160,167961600,168750000,169869312,170061120,170859375,172186884,172800000,174960000,175781250,176947200,177147000,179159040,180000000,181398528,182250000,184320000,184528125,186624000,187500000,188743680,188956800,189843750,191102976,191318760,192000000,194400000,195312500,196608000,196830000,199065600,199290375,200000000,201326592,201553920,202500000,204073344,204800000,205031250,207360000,209715200,209952000,210937500,212336640,212576400,214990848,215233605,216000000,218700000,221184000,221433750,223948800,225000000,226492416,226748160,227812500,229582512,230400000,233280000,234375000,235929600,236196000,238878720,239148450,240000000,241864704,243000000,244140625,245760000,246037500,248832000,250000000,251658240,251942400,253125000,254803968,255091680,256000000,258280326,259200000,262144000,262440000,263671875,265420800,265720500,268435456,268738560,270000000,272097792,273375000,276480000,279936000,281250000,283115520,283435200,284765625,286654464,286978140,288000000,291600000,292968750,294912000,295245000,298598400,300000000,301989888,302330880,303750000,306110016,307200000,307546875,311040000,312500000,314572800,314928000,316406250,318504960,318864600,320000000,322486272,324000000,327680000,328050000,331776000,332150625,335544320,335923200,337500000,339738624,340122240,341718750,344373768,345600000,349920000,351562500,353894400,354294000,358318080,358722675,360000000,362797056,364500000,368640000,369056250,373248000,375000000,377487360,377913600,379687500,382205952,382637520,384000000,387420489,388800000,390625000,393216000,393660000,398131200,398580750,400000000,402653184,403107840,405000000,408146688,409600000,410062500,414720000,419430400,419904000,421875000,424673280,425152800,429981696,430467210,432000000,437400000,439453125,442368000,442867500,447897600,450000000,452984832,453496320,455625000,459165024,460800000,466560000,468750000,471859200,472392000,474609375,477757440,478296900,480000000,483729408,486000000,488281250,491520000,492075000,497664000,500000000,503316480,503884800,506250000,509607936,510183360,512000000,512578125,516560652,518400000,524288000,524880000,527343750,530841600,531441000,536870912,537477120,540000000,544195584,546750000,552960000,553584375,559872000,562500000,566231040,566870400,569531250,573308928,573956280,576000000,583200000,585937500,589824000,590490000,597196800,597871125,600000000,603979776,604661760,607500000,612220032,614400000,615093750,622080000,625000000,629145600,629856000,632812500,637009920,637729200,640000000,644972544,645700815,648000000,655360000,656100000,663552000,664301250,671088640,671846400,675000000,679477248,680244480,683437500,688747536,691200000,699840000,703125000,707788800,708588000,716636160,717445350,720000000,725594112,729000000,732421875,737280000,738112500,746496000,750000000,754974720,755827200,759375000,764411904,765275040,768000000,774840978,777600000,781250000,786432000,787320000,791015625,796262400,797161500,800000000,805306368,806215680,810000000,816293376,819200000,820125000,829440000,838860800,839808000,843750000,849346560,850305600,854296875,859963392,860934420,864000000,874800000,878906250,884736000,885735000,895795200,900000000,905969664,906992640,911250000,918330048,921600000,922640625,933120000,937500000,943718400,944784000,949218750,955514880,956593800,960000000,967458816,972000000,976562500,983040000,984150000,995328000,996451875,1000000000,1006632960,1007769600,1012500000,1019215872,1020366720,1024000000,1025156250,1033121304,1036800000,1048576000,1049760000,1054687500,1061683200,1062882000,1073741824,1074954240,1076168025,1080000000,1088391168,1093500000,1105920000,1107168750,1119744000,1125000000,1132462080,1133740800,1139062500,1146617856,1147912560,1152000000,1162261467,1166400000,1171875000,1179648000,1180980000,1194393600,1195742250,1200000000,1207959552,1209323520,1215000000,1220703125,1224440064,1228800000,1230187500,1244160000,1250000000,1258291200,1259712000,1265625000,1274019840,1275458400,1280000000,1289945088,1291401630,1296000000,1310720000,1312200000,1318359375,1327104000,1328602500,1342177280,1343692800,1350000000,1358954496,1360488960,1366875000,1377495072,1382400000,1399680000,1406250000,1415577600,1417176000,1423828125,1433272320,1434890700,1440000000,1451188224,1458000000,1464843750,1474560000,1476225000,1492992000,1500000000,1509949440,1511654400,1518750000,1528823808,1530550080,1536000000,1537734375,1549681956,1555200000,1562500000,1572864000,1574640000,1582031250,1592524800,1594323000,1600000000,1610612736,1612431360,1620000000,1632586752,1638400000,1640250000,1658880000,1660753125,1677721600,1679616000,1687500000,1698693120,1700611200,1708593750,1719926784,1721868840,1728000000,1749600000,1757812500,1769472000,1771470000,1791590400,1793613375,1800000000,1811939328,1813985280,1822500000,1836660096,1843200000,1845281250,1866240000,1875000000,1887436800,1889568000,1898437500,1911029760,1913187600,1920000000,1934917632,1937102445,1944000000,1953125000,1966080000,1968300000,1990656000,1992903750,2000000000,2013265920,2015539200,2025000000,2038431744,2040733440,2048000000,2050312500,2066242608,2073600000,2097152000,2099520000,2109375000,2123366400}; return all[n-1]; } } //一开始以为能过的暴力法: class Solution { int UglyNumberNum = 0;//第几个丑数 public int nthUglyNumber(int n) { // List<Integer> UglyNums = new ArrayList<>(); int num = 1;//计算是否是丑数 int res = 0;//最终丑数 while(UglyNumberNum < n){ res = isUgly(num++); } // System.out.println(UglyNums); return res; } public int isUgly(int num){ if(num == 1) { UglyNumberNum++; return num; } int temp = num; while(num % 2== 0){ num /= 2; } while(num % 3 == 0){ num /= 3; } while(num % 5 == 0){ num /= 5; } if(num == 1){ UglyNumberNum++; return temp; } return 0; } } //看了官方题解的思路 -
179. 最大数
难度中等640收藏分享切换为英文接收动态反馈
给定一组非负整数
nums,重新排列每个数的顺序(每个数不可拆分)使之组成一个最大的整数。注意:输出结果可能非常大,所以你需要返回一个字符串而不是整数。
示例 1:
输入:nums = [10,2] 输出:"210"示例 2:
输入:nums = [3,30,34,5,9] 输出:"9534330"示例 3:
输入:nums = [1] 输出:"1"示例 4:
输入:nums = [10] 输出:"10"提示:
1 <= nums.length <= 1000 <= nums[i] <= 109
//要认真审题,数字会非常大,所以需要用Long.parseLong(String s)去转成可以比较的数字而不能用Integer.parseInt(String s)。 class Solution { public String largestNumber(int[] nums) { //排序拼接即可。不过排序是按照最左数字降序排列;如果两个最左数字相同,就按照拼接之后的数字谁大,就谁先排在前面。 int j = nums.length; record[] records = new record[j]; for(int i = 0;i < j;i++){ records[i] = new record(nums[i],i); } Arrays.sort(records, new Comparator<record>() { @Override public int compare(record o1, record o2) { if(zuo(o1.number) == zuo(o2.number)){ String e1 = Integer.toString(o1.number); String e2 = Integer.toString(o2.number); Long temp1 = Long.parseLong(e1+""+e2);//测试用例的999999991过于大,无法转成Integer,最多转7位,所以要用Long Long temp2 = Long.parseLong(e2+""+e1); return temp2 - temp1 > 0 ? 1 : -1; } else return zuo(o2.number) - zuo(o1.number); } }); String s = new String(); for(record record1 : records){ s = s + record1.number; } // if(s.equals("00")) return "0";//测试用例还有[0,0]和[0,0,0],吐了 boolean flag = false; for(int i = 0;i < j;i++){ if(s.charAt(i) != '0'){ flag = true; } } if(flag) return s; else return "0"; //其实这里看了官方题解才知道,直接判断s.charAt(0)=='0'就可以判断的。 } //返回最左数字 public static int zuo(int num){ while(num > 0){ if(num < 10){ break; } num /= 10; } return num; } //拼接给定的个位数字num2到num1的后面,如(1,2)->12 public static int pinjie(int num1,int num2){ return num1 * 10 + num2; } } class record{ int number;//nums的元素 int index;//下标 public record(int number, int index) { this.number = number; this.index = index; } } -
783. 二叉搜索树节点最小距离
难度简单137收藏分享切换为英文接收动态反馈
给你一个二叉搜索树的根节点
root,返回 树中任意两不同节点值之间的最小差值 。注意:本题与 530:https://leetcode-cn.com/problems/minimum-absolute-difference-in-bst/ 相同
示例 1:

输入:root = [4,2,6,1,3] 输出:1示例 2:

输入:root = [1,0,48,null,null,12,49] 输出:1提示:
- 树中节点数目在范围
[2, 100]内 0 <= Node.val <= 105
/** * Definition for a binary tree node. * public class TreeNode { * int val; * TreeNode left; * TreeNode right; * TreeNode() {} * TreeNode(int val) { this.val = val; } * TreeNode(int val, TreeNode left, TreeNode right) { * this.val = val; * this.left = left; * this.right = right; * } * } */ class Solution { int result = 100001; public int minDiffInBST(TreeNode root) { //因为是二叉搜索树,所以只需要中序遍历(这样就可以得到升序数组),再比较相邻节点的最小差值维护即可。 ArrayList<Integer> res = new ArrayList<>(); dfs(root,res); // for(int i : res){ // System.out.println(i); // } for(int i = 1,j = res.size();i < j;i++){ // System.out.println(res.get(i)-res.get(i-1)); result = Math.min(result,res.get(i)-res.get(i-1)); } return result; } void dfs(TreeNode root,ArrayList<Integer> res){ if(root == null){ return; } dfs(root.left,res); res.add(root.val); dfs(root.right,res); } } - 树中节点数目在范围
-
208. 实现 Trie (前缀树)
难度中等
Trie(发音类似 "try")或者说 前缀树 是一种树形数据结构,用于高效地存储和检索字符串数据集中的键。这一数据结构有相当多的应用情景,例如自动补完和拼写检查。
请你实现 Trie 类:
Trie()初始化前缀树对象。void insert(String word)向前缀树中插入字符串word。boolean search(String word)如果字符串word在前缀树中,返回true(即,在检索之前已经插入);否则,返回false。boolean startsWith(String prefix)如果之前已经插入的字符串word的前缀之一为prefix,返回true;否则,返回false。
示例:
输入 ["Trie", "insert", "search", "search", "startsWith", "insert", "search"] [[], ["apple"], ["apple"], ["app"], ["app"], ["app"], ["app"]] 输出 [null, null, true, false, true, null, true] 解释 Trie trie = new Trie(); trie.insert("apple"); trie.search("apple"); // 返回 True trie.search("app"); // 返回 False trie.startsWith("app"); // 返回 True trie.insert("app"); trie.search("app"); // 返回 True提示:
1 <= word.length, prefix.length <= 2000word和prefix仅由小写英文字母组成insert、search和startsWith调用次数 总计 不超过3 * 104次
class Trie { Trie[] chars;//存储下一个节点,下标表示'a'~'z'字母(0~25) boolean isEnd;//表示是否为字符串终止处 /** Initialize your data structure here. */ public Trie() { chars = new Trie[26]; isEnd = false; } /** Inserts a word into the trie. */ public void insert(String word) { Trie tire = this; for(int i = 0,j = word.length();i < j;i++){ if(tire.chars[word.charAt(i) - 'a'] == null){ tire.chars[word.charAt(i) - 'a'] = new Trie(); } tire = tire.chars[word.charAt(i) - 'a']; } tire.isEnd = true; } /** Returns if the word is in the trie. */ public boolean search(String word) { Trie tire = this; for(int i = 0,j = word.length();i < j;i++){ if(tire.chars[word.charAt(i) - 'a'] == null){ return false; } tire = tire.chars[word.charAt(i) - 'a']; } if(tire.isEnd == true){ return true; } else{ return false; } } /** Returns if there is any word in the trie that starts with the given prefix. */ public boolean startsWith(String prefix) { Trie tire = this; for(int i = 0,j = prefix.length();i < j;i++){ if(tire.chars[prefix.charAt(i) - 'a'] == null){ return false; } tire = tire.chars[prefix.charAt(i) - 'a']; } return true; } } /** * Your Trie object will be instantiated and called as such: * Trie obj = new Trie(); * obj.insert(word); * boolean param_2 = obj.search(word); * boolean param_3 = obj.startsWith(prefix); */ -
213. 打家劫舍 II
难度中等
你是一个专业的小偷,计划偷窃沿街的房屋,每间房内都藏有一定的现金。这个地方所有的房屋都 围成一圈 ,这意味着第一个房屋和最后一个房屋是紧挨着的。同时,相邻的房屋装有相互连通的防盗系统,如果两间相邻的房屋在同一晚上被小偷闯入,系统会自动报警 。
给定一个代表每个房屋存放金额的非负整数数组,计算你 在不触动警报装置的情况下 ,能够偷窃到的最高金额。
示例 1:
输入:nums = [2,3,2] 输出:3 解释:你不能先偷窃 1 号房屋(金额 = 2),然后偷窃 3 号房屋(金额 = 2), 因为他们是相邻的。示例 2:
输入:nums = [1,2,3,1] 输出:4 解释:你可以先偷窃 1 号房屋(金额 = 1),然后偷窃 3 号房屋(金额 = 3)。 偷窃到的最高金额 = 1 + 3 = 4 。示例 3:
输入:nums = [0] 输出:0提示:
1 <= nums.length <= 1000 <= nums[i] <= 1000
class Solution { public int rob(int[] nums) { //f(i)表示偷窃第i个房屋的最大金额,g(i)表示不偷窃第i个房屋的最大金额 //f(i) = g(i+1)+nums[i] ,g(i) = Math.max(f(i+1),g(i+1)) //两种情况,偷窃范围在[0,n-2]和[1,n-1]————偷窃第一间就无法偷最后一间,不偷窃第一间就可以偷最后一间 int len = nums.length; if(len == 1){ //只有一间直接偷,不会报警 return nums[0]; } if(len == 2){ //只有两间偷最值钱的 return Math.max(nums[0],nums[1]); } int[] f1 = new int[len]; int[] g1 = new int[len]; f1[len-2] = nums[len-2]; for(int i = len-3;i >= 0;i--){ g1[i] = Math.max(f1[i+1],g1[i+1]); f1[i] = g1[i+1]+nums[i]; } int res1 = Math.max(f1[0],g1[0]); //偷第一间的最大金额 int[] f2 = new int[len]; int[] g2 = new int[len]; f2[len-1] = nums[len-1]; for(int i = len-2;i >= 1;i--){ g2[i] = Math.max(f2[i+1],g2[i+1]); f2[i] = g2[i+1]+nums[i]; } int res2 = Math.max(f2[1],g2[1]); //不偷第一间的最大金额 return Math.max(res1,res2); } } -
87. 扰乱字符串
难度困难334收藏分享切换为英文接收动态反馈
使用下面描述的算法可以扰乱字符串
s得到字符串t:- 如果字符串的长度为 1 ,算法停止
- 如果字符串的长度 > 1 ,执行下述步骤:
- 在一个随机下标处将字符串分割成两个非空的子字符串。即,如果已知字符串
s,则可以将其分成两个子字符串x和y,且满足s = x + y。 - 随机 决定是要「交换两个子字符串」还是要「保持这两个子字符串的顺序不变」。即,在执行这一步骤之后,
s可能是s = x + y或者s = y + x。 - 在
x和y这两个子字符串上继续从步骤 1 开始递归执行此算法。
- 在一个随机下标处将字符串分割成两个非空的子字符串。即,如果已知字符串
给你两个 长度相等 的字符串
s1和s2,判断s2是否是s1的扰乱字符串。如果是,返回true;否则,返回false。示例 1:
输入:s1 = "great", s2 = "rgeat" 输出:true 解释:s1 上可能发生的一种情形是: "great" --> "gr/eat" // 在一个随机下标处分割得到两个子字符串 "gr/eat" --> "gr/eat" // 随机决定:「保持这两个子字符串的顺序不变」 "gr/eat" --> "g/r / e/at" // 在子字符串上递归执行此算法。两个子字符串分别在随机下标处进行一轮分割 "g/r / e/at" --> "r/g / e/at" // 随机决定:第一组「交换两个子字符串」,第二组「保持这两个子字符串的顺序不变」 "r/g / e/at" --> "r/g / e/ a/t" // 继续递归执行此算法,将 "at" 分割得到 "a/t" "r/g / e/ a/t" --> "r/g / e/ a/t" // 随机决定:「保持这两个子字符串的顺序不变」 算法终止,结果字符串和 s2 相同,都是 "rgeat" 这是一种能够扰乱 s1 得到 s2 的情形,可以认为 s2 是 s1 的扰乱字符串,返回 true示例 2:
输入:s1 = "abcde", s2 = "caebd" 输出:false示例 3:
输入:s1 = "a", s2 = "a" 输出:true提示:
s1.length == s2.length1 <= s1.length <= 30s1和s2由小写英文字母组成
第一次一看就懵逼的每日一题。
看到递归就想到回溯:
class Solution { public boolean isScramble(String s1, String s2) { return backroll(s1,s2); } boolean backroll(String temp1,String temp2){//判断s1的[0,i),[i,n)是否分别与s2的[0,n-i),[i,n)或者[0,n-i),[n-i,n)匹配 if(temp1.equals(temp2)){//截止条件很难判断,匹配到只有一个元素的时候不相等就是不匹配 return true; } int len = temp1.length(); for(int i = 1;i < len;i++){ String a = temp1.substring(0,i),b = temp1.substring(i); String c = temp2.substring(0,i),d = temp2.substring(i); if(backroll(a,c) && backroll(b,d)){ return true; } String e = temp2.substring(0,len-i),f = temp2.substring(len-i); if(backroll(a,f) && backroll(b,e)){ return true; } } return false;//遍历了s1[0,]1~len]都没有一个true返回,说明没有一个字符串是和s2对应的 } }但是发现样例一大就超时,需要剪枝。
对两个字符串进行词频分析,因为只要是不是字符一样数量不一致就说明不是置换过来的,可以剪枝,于是:
class Solution { public boolean isScramble(String s1, String s2) { return backroll(s1,s2); } boolean backroll(String temp1,String temp2){//判断s1的[0,i),[i,n)是否分别与s2的[0,n-i),[i,n)或者[0,n-i),[n-i,n)匹配 if(temp1.equals(temp2)){//截止条件很难判断,匹配到只有一个元素的时候不相等就是不匹配 return true; } if(check(temp1,temp2) == false){ return false; } int len = temp1.length(); for(int i = 1;i < len;i++){ String a = temp1.substring(0,i),b = temp1.substring(i); String c = temp2.substring(0,i),d = temp2.substring(i); if(backroll(a,c) && backroll(b,d)){ return true; } String e = temp2.substring(0,len-i),f = temp2.substring(len-i); if(backroll(a,f) && backroll(b,e)){ return true; } } return false;//遍历了s1[0,]1~len]都没有一个true返回,说明没有一个字符串是和s2对应的 } boolean check(String temp1,String temp2){ int len1 = temp1.length(); int len2 = temp2.length(); if(len1 != len2){ return false; } int[] res1 = new int[27]; int[] res2 = new int[27]; //桶排序比较两个字符串的词频是否一样 for(int i = 0;i < len1;i++){ res1[temp1.charAt(i)-'a']++; res2[temp2.charAt(i)-'a']++; } for(int i = 0;i < 27;i++){ if(res1[i] != res2[i]) { return false; } } return true; } }结果在最后两个测试用例的时候倒下:
状态:超出时间限制 最后执行的输入: "eebaacbcbcadaaedceaaacadccd" "eadcaacabaddaceacbceaabeccd"加了我以为的记忆化搜索,还是会超时:
class Solution { public boolean isScramble(String s1, String s2) { int sumlen = s1.length(); int[][][] dp = new int[sumlen+1][sumlen+1][sumlen+1]; return backroll(0,0,sumlen,s1,s2,dp); } boolean backroll(int s1start,int s2start,int length,String s1,String s2,int[][][] dp){//判断s1的[0,i),[i,n)是否分别与s2的[0,i),[i,n)或者[0,n-i),[n-i,n)匹配 if(length == 1 && s1.substring(s1start,s1start+1).equals(s2.substring(s2start,s2start+1))){//截止条件很难判断,匹配到只有一个元素的时候不相等就是不匹配 return true; } if(check(s1.substring(s1start,s1start+length),s2.substring(s2start,s2start+length)) == false){ return false; } for(int i = 1;i < length;i++){ if((dp[s1start][s2start][i] == 1 && dp[s1start][s2start+i][length-i] == 1) || backroll(s1start,s2start,i,s1,s2,dp) && backroll(s1start+i,s2start+i,length-i,s1,s2,dp)){ dp[s1start][s2start][length] = 1; return true; } if((dp[s1start][s2start+length-i][i] == 1 && dp[s1start+i][s2start][length-i] == 1) || backroll(s1start,s2start+length-i,i,s1,s2,dp) && backroll(s1start+i,s2start,length-i,s1,s2,dp)){ dp[s1start][s2start][length] = 1; return true; } } return false;//遍历了s1[0,1~len]都没有一个true返回,说明没有一个字符串是和s2对应的 } boolean check(String temp1,String temp2){ int len1 = temp1.length(); int len2 = temp2.length(); if(len1 != len2){ return false; } int[] res1 = new int[27]; int[] res2 = new int[27]; //桶排序比较两个字符串的词频是否一样 for(int i = 0;i < len1;i++){ res1[temp1.charAt(i)-'a']++; res2[temp2.charAt(i)-'a']++; } for(int i = 0;i < 27;i++){ if(res1[i] != res2[i]) { return false; } } return true; } } -
220. 存在重复元素 III
难度中等
给你一个整数数组
nums和两个整数k和t。请你判断是否存在 两个不同下标i和j,使得abs(nums[i] - nums[j]) <= t,同时又满足abs(i - j) <= k。如果存在则返回
true,不存在返回false。示例 1:
输入:nums = [1,2,3,1], k = 3, t = 0 输出:true示例 2:
输入:nums = [1,0,1,1], k = 1, t = 2 输出:true示例 3:
输入:nums = [1,5,9,1,5,9], k = 2, t = 3 输出:false提示:
0 <= nums.length <= 2 * 104-231 <= nums[i] <= 231 - 10 <= k <= 1040 <= t <= 231 - 1
一开始以为很简单,然后就被教育了。这题主要是卡你两个地方:1. nums[i]-nums[j]可能会很大,大到超出int范围(两个int数相加减一定要考虑溢出的问题),解决方法就是BigInteger。2. nums的长度可能会很大,比如一个测试用例里的十万长度。
//我以为解决了大数溢出就行了。。。结果,压根不能for(for(length))这样遍历 import java.math.BigInteger; class Solution { public boolean containsNearbyAlmostDuplicate(int[] nums, int k, int t) { int length = nums.length; for(int i = 0;i < length;i++){ for(int j = i+1;j < length;j++){//用例有一个十万长度数组过不去 System.out.println("0"); if(nums[i] < 10000000 && nums[j] < 10000000){ if(Math.abs(nums[i]-nums[j]) <= t && Math.abs(i-j) <= k){ System.out.println("1"); return true; } } else { System.out.println("2"); BigInteger res1 = new BigInteger(nums[i]+""); BigInteger res2 = new BigInteger(nums[j]+""); BigInteger rest = new BigInteger(t+""); if(res1.subtract(res2).abs().compareTo(rest) <= 0 && Math.abs(i - j) <= k){//[-2147483648,2147483647]会计算爆栈变成负数, // System.out.println("i="+i+" j="+j); // System.out.println("res="+res1+" Math.abs(nums[i] - nums[j])="+Math.abs(res1)+" Math.abs(i - j)="+Math.abs(i - j)); return true; } } } } return false; } }看了宫水三叶的题解才发现诸如数组比较判断的题,直接暴力搜索是不行的,一旦长度达到十万就会超限了,必须考虑O(n)的解法。比如滑动窗口:
class Solution { public boolean containsNearbyAlmostDuplicate(int[] nums, int k, int t) { int length = nums.length; //题目的意思是在[i-k,i]范围内([i-k,i+k]太大,反正是遍历i所以只需要取前一段),是否存在[nums[i]-t,nums[i]+t]的nums[j]。 //TreeSet是有序集合,放进去了就自动排序。 TreeSet<Long> ts = new TreeSet<>(); for(int i = 0;i < length;i++){ Long res1 = ts.floor(nums[i]*1L);//小于等于nums[i]的最大值 Long res2 = ts.ceiling(nums[i]*1L);//大于等于nums[i]的最小值 if(res1 != null && nums[i] - res1 <= t){ return true; } if(res2 != null && res2 - nums[i] <= t){ return true; } ts.add(nums[i]*1L); if(i >= k){ ts.remove(nums[i-k]*1L);//由于i是从0开始遍历的,所以i-k前面的TreeSet全部不要,就不会出现abs(nums[i] - nums[j]) <= t但是abs(i - j) >= k的情况了。 } } return false; } } -
26. 删除有序数组中的重复项
难度简单
给你一个有序数组
nums,请你 原地 删除重复出现的元素,使每个元素 只出现一次 ,返回删除后数组的新长度。不要使用额外的数组空间,你必须在 原地 修改输入数组 并在使用 O(1) 额外空间的条件下完成。
说明:
为什么返回数值是整数,但输出的答案是数组呢?
请注意,输入数组是以「引用」方式传递的,这意味着在函数里修改输入数组对于调用者是可见的。
你可以想象内部操作如下:
// nums 是以“引用”方式传递的。也就是说,不对实参做任何拷贝 int len = removeDuplicates(nums); // 在函数里修改输入数组对于调用者是可见的。 // 根据你的函数返回的长度, 它会打印出数组中 该长度范围内 的所有元素。 for (int i = 0; i < len; i++) { print(nums[i]); }示例 1:
输入:nums = [1,1,2] 输出:2, nums = [1,2] 解释:函数应该返回新的长度 2 ,并且原数组 nums 的前两个元素被修改为 1, 2 。不需要考虑数组中超出新长度后面的元素。示例 2:
输入:nums = [0,0,1,1,1,2,2,3,3,4] 输出:5, nums = [0,1,2,3,4] 解释:函数应该返回新的长度 5 , 并且原数组 nums 的前五个元素被修改为 0, 1, 2, 3, 4 。不需要考虑数组中超出新长度后面的元素。提示:
0 <= nums.length <= 3 * 104-104 <= nums[i] <= 104nums已按升序排列
今天也是不细心的一天,写得代码总是通不过,还很繁琐:
//未通过,反面教材 class Solution { public int removeDuplicates(int[] nums) { //nums 已按升序排列 int len = nums.length; int res = 0; //i是重复区间的左指针,j是右指针 //i检测是否nums[x] == nums[x+1],一旦检测到就i = x+1;j=i,然后检测重复区间长度,i开始,一直到nums[y] != nums[i]结束,j = y。这样重复区间就是[i,j) int i = 0,j = i; int max = 0; for(int x = 0;x < len;x++){ //确定i和j的(即重复区间长度) if(x+1 < len && nums[x] == nums[x+1]){ i = x+1; int y = i; while(y < len && nums[y] == nums[i]){ y++; } j = y; } System.out.println("\n重复区间长度="+(j-i)+" ["+i+","+j+")"); max = max > (j-i) ? max : j-i; //覆盖,将[j,len-1]移到[i,len-1] for(int f = i;f+j-i < len;f++){ System.out.println("nums["+f+"]="+"nums["+(f+j-i)+"],即"+nums[f]+"="+nums[f+j-i]+";"); System.out.println("覆盖前"); for(int d = 0;d < len;d++){ System.out.print(nums[d]+" "); } nums[f] = nums[f+j-i]; System.out.println("\n覆盖后"); for(int d = 0;d < len;d++){ System.out.print(nums[d]+" "); } } } System.out.println(len-max); return len; } }宫水三叶的代码就是优雅:
class Solution { public int removeDuplicates(int[] nums) { //双指针,j表示有效数组的最终位置,i表示当前遍历的位置 int len = nums.length; int j = 0; for(int i = 0;i < len;i++){ if(nums[j] != nums[i]){ nums[++j] = nums[i]; } } return j+1; } }我一开始只想到要确定重复区间i,j),然后维护和去重的过程很繁琐,还要确定最终的数组长度,于是给自己搞蒙了。
而宫水大佬的解法是维护两个指针,j表示当前有效数组最终位置(nums[0]是不可改变的),i表示当前遍历的位置,相当于哨兵,每次比较nums[i]和nums[j]是否相等就知道j要不要移动了。
得出的教训是:题目要什么就直截了当的计算什么,搞什么区间都是走弯路,给自己徒添复杂。
-
27. 移除元素
难度简单865收藏分享切换为英文接收动态反馈
给你一个数组
nums和一个值val,你需要 原地 移除所有数值等于val的元素,并返回移除后数组的新长度。不要使用额外的数组空间,你必须仅使用
O(1)额外空间并 原地 修改输入数组。元素的顺序可以改变。你不需要考虑数组中超出新长度后面的元素。
说明:
为什么返回数值是整数,但输出的答案是数组呢?
请注意,输入数组是以「引用」方式传递的,这意味着在函数里修改输入数组对于调用者是可见的。
你可以想象内部操作如下:
// nums 是以“引用”方式传递的。也就是说,不对实参作任何拷贝 int len = removeElement(nums, val); // 在函数里修改输入数组对于调用者是可见的。 // 根据你的函数返回的长度, 它会打印出数组中 该长度范围内 的所有元素。 for (int i = 0; i < len; i++) { print(nums[i]); }示例 1:
输入:nums = [3,2,2,3], val = 3 输出:2, nums = [2,2] 解释:函数应该返回新的长度 2, 并且 nums 中的前两个元素均为 2。你不需要考虑数组中超出新长度后面的元素。例如,函数返回的新长度为 2 ,而 nums = [2,2,3,3] 或 nums = [2,2,0,0],也会被视作正确答案。示例 2:
输入:nums = [0,1,2,2,3,0,4,2], val = 2 输出:5, nums = [0,1,4,0,3] 解释:函数应该返回新的长度 5, 并且 nums 中的前五个元素为 0, 1, 3, 0, 4。注意这五个元素可为任意顺序。你不需要考虑数组中超出新长度后面的元素。提示:
0 <= nums.length <= 1000 <= nums[i] <= 500 <= val <= 100
暴力法:
class Solution { public int removeElement(int[] nums, int val) { int len = nums.length; int temp = 0;//重复元素个数 for(int right = 0;right < len-temp;){ if(val == nums[right]){ temp++; for(int left = right;left+1 < len;left++){ nums[left] = nums[left+1]; } } else{ right++; } } return len-temp; } }正宗双指针:(right检测到是val就执行覆盖,不是val就right++,然后left和right隔着的就是重复元素的个数,到这里就已经是双指针了)
class Solution { public int removeElement(int[] nums, int val) { int len = nums.length; //right是哨兵,left是有效数组的最终位置。找到第一个符合题意的下表开始,右指针不断赋给左指针直到右指针到达边界 int right = 0,left = right; for(;right < len;){ if(nums[right] == val){ while(right < len && nums[right] == val){ right++; } } else{ nums[left] = nums[right]; left++; right++; } } return left; } } -
28. 实现 strStr()
难度简单
实现 strStr() 函数。
给你两个字符串
haystack和needle,请你在haystack字符串中找出needle字符串出现的第一个位置(下标从 0 开始)。如果不存在,则返回-1。说明:
当
needle是空字符串时,我们应当返回什么值呢?这是一个在面试中很好的问题。对于本题而言,当
needle是空字符串时我们应当返回 0 。这与 C 语言的 strstr() 以及 Java 的 indexOf() 定义相符。示例 1:
输入:haystack = "hello", needle = "ll" 输出:2示例 2:
输入:haystack = "aaaaa", needle = "bba" 输出:-1示例 3:
输入:haystack = "", needle = "" 输出:0提示:
0 <= haystack.length, needle.length <= 5 * 104haystack和needle仅由小写英文字符组成
暴力法,while其实很多时候比for要好,什么时候呢?就是遍历的指针不能无脑++、参与了很多逻辑计算的时候。
class Solution { public int strStr(String haystack, String needle) { //O(n^2) int len1 = haystack.length(),len2 = needle.length(); if(len2 == 0){ return 0; } if(len2 > len1){ return -1; } int i = 0; while(i < len1){ if(haystack.charAt(i) == needle.charAt(0)){ // System.out.println(i); int j = 1; boolean flag = true; int temp = i+1; while(j < len2){ if(temp >= len1 || haystack.charAt(temp) != needle.charAt(j)){ flag = false; break; } temp++; j++; } if(flag == true){ return i; } } i++; } return -1; } }通过了但是不太理想,只超越了5%的人,O(n^2)复杂度和charAt()可能导致耗时过大,不过这解法没啥好讨论的,暴力就完事。
看了宫水三叶的题解,提到了KMP算法(专门用于解决字符串匹配的问题,还提到了Manacher算法,专门用于解决回文串问题,都是知识点必须拿下):
若本次匹配失败,则下次查看匹配串有无相同的前缀和后缀,若有就直接开始匹配原串的后缀的下一个位置是否与匹配串匹配,直接跳过后缀区间元素为起点的匹配循环(比如后缀为[i,j],不论是否匹配,都不用探讨(i,j]开始的匹配循环)。但是难在不匹配后下次匹配从哪开始,题解是维护好一个只与匹配串相关的next数组:
-
91. 解码方法
难度中等
一条包含字母
A-Z的消息通过以下映射进行了 编码 :'A' -> 1 'B' -> 2 ... 'Z' -> 26要 解码 已编码的消息,所有数字必须基于上述映射的方法,反向映射回字母(可能有多种方法)。例如,
"11106"可以映射为:"AAJF",将消息分组为(1 1 10 6)"KJF",将消息分组为(11 10 6)
注意,消息不能分组为
(1 11 06),因为"06"不能映射为"F",这是由于"6"和"06"在映射中并不等价。给你一个只含数字的 非空 字符串
s,请计算并返回 解码 方法的 总数 。题目数据保证答案肯定是一个 32 位 的整数。
示例 1:
输入:s = "12" 输出:2 解释:它可以解码为 "AB"(1 2)或者 "L"(12)。示例 2:
输入:s = "226" 输出:3 解释:它可以解码为 "BZ" (2 26), "VF" (22 6), 或者 "BBF" (2 2 6) 。示例 3:
输入:s = "0" 输出:0 解释:没有字符映射到以 0 开头的数字。 含有 0 的有效映射是 'J' -> "10" 和 'T'-> "20" 。 由于没有字符,因此没有有效的方法对此进行解码,因为所有数字都需要映射。示例 4:
输入:s = "06" 输出:0 解释:"06" 不能映射到 "F" ,因为字符串含有前导 0("6" 和 "06" 在映射中并不等价)。提示:
1 <= s.length <= 100s只包含数字,并且可能包含前导零。
一看到做选择,还以为是回溯,尝试回溯,发现由于要记录的只是从头开始转换的结果而不是子集,所以回溯无法完成,只能用动态规划:
class Solution { public int numDecodings(String s) { //dp[i] 表示以i为结尾的可能转换种数,dp[i] = dp[i-1] + dp[i-2]。 int len = s.length(); int[] dp = new int[len]; if(Integer.parseInt(s.charAt(0)+"") != 0){ dp[0] = 1; } else{ return 0; } if(len ==1){ return 1; } if(Integer.parseInt(s.charAt(1)+"") != 0){ if(Integer.parseInt(s.substring(0,2)) > 26){ dp[1] = 1;//3,1 } else{ dp[1] = 2;//2,4 } } else{ if(Integer.parseInt(s.substring(0,2)) > 26){ dp[1] = 0;//3,0 } else{ dp[1] = 1;//2,0 } } for(int i = 2;i < len;i++){ //一个字符符合,dp[i] += dp[i-1]+1; //两个字符符合,dp[i] += dp[i-2]+1; int num1 = Integer.parseInt(s.charAt(i)+""); if(num1 != 0){ dp[i] += dp[i-1]; } if(i - 2 < 0){ continue; } int num2 = Integer.parseInt(s.substring(i-1,i+1)); if(num2 <= 26 && num2 > 9){ dp[i] += dp[i-2]; } } // for(int i = 0;i < len ;i++){ // System.out.println(dp[i]); // } return dp[len-1]; } }官方题解的比较简洁和高效:
class Solution { public int numDecodings(String s) { int n = s.length(); int[] f = new int[n + 1]; f[0] = 1; for (int i = 1; i <= n; ++i) { if (s.charAt(i - 1) != '0') { f[i] += f[i - 1]; } if (i > 1 && s.charAt(i - 2) != '0' && ((s.charAt(i - 2) - '0') * 10 + (s.charAt(i - 1) - '0') <= 26)) { f[i] += f[i - 2]; } } return f[n]; } } 作者:LeetCode-Solution 链接:https://leetcode-cn.com/problems/decode-ways/solution/jie-ma-fang-fa-by-leetcode-solution-p8np/ 来源:力扣(LeetCode) 著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。 -
363. 矩形区域不超过 K 的最大数值和
难度困难
给你一个
m x n的矩阵matrix和一个整数k,找出并返回矩阵内部矩形区域的不超过k的最大数值和。题目数据保证总会存在一个数值和不超过
k的矩形区域。示例 1:
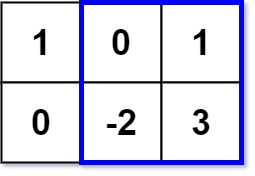
输入:matrix = [[1,0,1],[0,-2,3]], k = 2 输出:2 解释:蓝色边框圈出来的矩形区域 [[0, 1], [-2, 3]] 的数值和是 2,且 2 是不超过 k 的最大数字(k = 2)。示例 2:
输入:matrix = [[2,2,-1]], k = 3 输出:3提示:
m == matrix.lengthn == matrix[i].length1 <= m, n <= 100-100 <= matrix[i][j] <= 100-105 <= k <= 105
进阶:如果行数远大于列数,该如何设计解决方案?
-
368. 最大整除子集
难度中等311
给你一个由 无重复 正整数组成的集合
nums,请你找出并返回其中最大的整除子集answer,子集中每一元素对(answer[i], answer[j])都应当满足:answer[i] % answer[j] == 0,或answer[j] % answer[i] == 0
如果存在多个有效解子集,返回其中任何一个均可。
示例 1:
输入:nums = [1,2,3] 输出:[1,2] 解释:[1,3] 也会被视为正确答案。示例 2:
输入:nums = [1,2,4,8] 输出:[1,2,4,8]提示:
1 <= nums.length <= 10001 <= nums[i] <= 2 * 109nums中的所有整数 互不相同
-
377. 组合总和 Ⅳ
难度中等376
给你一个由 不同 整数组成的数组
nums,和一个目标整数target。请你从nums中找出并返回总和为target的元素组合的个数。题目数据保证答案符合 32 位整数范围。
示例 1:
输入:nums = [1,2,3], target = 4 输出:7 解释: 所有可能的组合为: (1, 1, 1, 1) (1, 1, 2) (1, 2, 1) (1, 3) (2, 1, 1) (2, 2) (3, 1) 请注意,顺序不同的序列被视作不同的组合。示例 2:
输入:nums = [9], target = 3 输出:0提示:
1 <= nums.length <= 2001 <= nums[i] <= 1000nums中的所有元素 互不相同1 <= target <= 1000
进阶:如果给定的数组中含有负数会发生什么?问题会产生何种变化?如果允许负数出现,需要向题目中添加哪些限制条件?
采用类变量sum居然会超时(卡在nums=[1,2,3],target=23):
class Solution { int sum; public int combinationSum4(int[] nums, int target) { int n = nums.length; backroll(0,target,n,nums); return sum; } void backroll(int now,int target,int n,int[] nums){//now是目前已经加的值 if(now == target){ sum++; return; } if(now > target){ return; } for(int i = 0;i < n;i++){ now+=nums[i]; backroll(now,target,n,nums); now-=nums[i]; } } }那么就要记忆化搜索,,,,等等这题连记忆化搜索我都觉得没法做(哪有需要记忆的数组之类的呀,直接是一个sum,这怎么优化?)于是只能考虑动态规划:
大佬的题解再次刷新了我的认知,动态规划状态转移的上一个状态不一定是i-1、j-1的,也可以是j-u,即上一个刚好要加当前nums[]元素就可以完美得出当前状态的状态,就是上一个状态(不止一个);换句话说,所有这些刚好加上当前元素就能构成当前元素结尾的方案只要加起来,就是当前元素的总方案。
dp[i][j]是指组合长度为i、总和为j的方案数。
class Solution { public int combinationSum4(int[] nums, int target) { int len = target;//这里不懂为什么是target不是nums.length int[][] dp = new int[len+1][target+1]; dp[0][0] = 1; int ans = 0; for(int i = 1;i <= len;i++){ for(int j = 0;j <= target;j++){ for(int u : nums){ //因为每次都可以任意重复选。 if(j >= u){ dp[i][j]+=dp[i-1][j-u]; } } ans+=dp[i][target]; } } return ans; } }另外简化版本,并且简单易懂:(dp[i]表示能组合出i的数量)
class Solution { public int combinationSum4(int[] nums, int target) { int[] dp = new int[target+1]; dp[0] = 1; for(int i = 1;i <= target;i++){ //注意迭代的是target for(int n : nums){ if(n <= i){ dp[i] += dp[i-n]; //这里很重要 } } } return dp[target]; } } -
897. 递增顺序搜索树
难度简单
给你一棵二叉搜索树,请你 按中序遍历 将其重新排列为一棵递增顺序搜索树,使树中最左边的节点成为树的根节点,并且每个节点没有左子节点,只有一个右子节点。
示例 1:
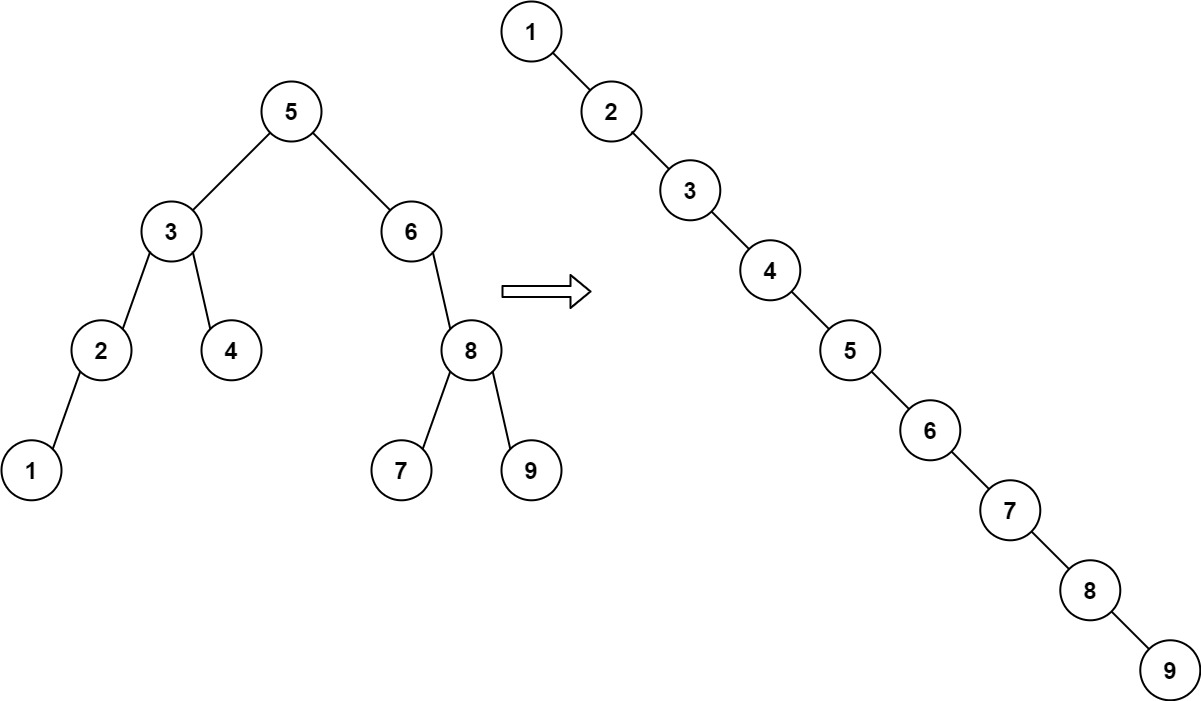
输入:root = [5,3,6,2,4,null,8,1,null,null,null,7,9] 输出:[1,null,2,null,3,null,4,null,5,null,6,null,7,null,8,null,9]示例 2:
输入:root = [5,1,7] 输出:[1,null,5,null,7]提示:
- 树中节点数的取值范围是
[1, 100] 0 <= Node.val <= 1000
/** * Definition for a binary tree node. * public class TreeNode { * int val; * TreeNode left; * TreeNode right; * TreeNode() {} * TreeNode(int val) { this.val = val; } * TreeNode(int val, TreeNode left, TreeNode right) { * this.val = val; * this.left = left; * this.right = right; * } * } */ class Solution { TreeNode newRoot = new TreeNode(); TreeNode temp = newRoot; public TreeNode increasingBST(TreeNode root) { backroll(root); return temp.right; } void backroll(TreeNode root){ if(root == null){ return; } backroll(root.left); newRoot.right = new TreeNode(root.val); while(newRoot.right != null){ newRoot = newRoot.right; } backroll(root.right); } } - 树中节点数的取值范围是
-
1011. 在 D 天内送达包裹的能力
难度中等
传送带上的包裹必须在 D 天内从一个港口运送到另一个港口。
传送带上的第
i个包裹的重量为weights[i]。每一天,我们都会按给出重量的顺序往传送带上装载包裹。我们装载的重量不会超过船的最大运载重量。返回能在
D天内将传送带上的所有包裹送达的船的最低运载能力。示例 1:
输入:weights = [1,2,3,4,5,6,7,8,9,10], D = 5 输出:15 解释: 船舶最低载重 15 就能够在 5 天内送达所有包裹,如下所示: 第 1 天:1, 2, 3, 4, 5 第 2 天:6, 7 第 3 天:8 第 4 天:9 第 5 天:10 请注意,货物必须按照给定的顺序装运,因此使用载重能力为 14 的船舶并将包装分成 (2, 3, 4, 5), (1, 6, 7), (8), (9), (10) 是不允许的。示例 2:
输入:weights = [3,2,2,4,1,4], D = 3 输出:6 解释: 船舶最低载重 6 就能够在 3 天内送达所有包裹,如下所示: 第 1 天:3, 2 第 2 天:2, 4 第 3 天:1, 4示例 3:
输入:weights = [1,2,3,1,1], D = 4 输出:3 解释: 第 1 天:1 第 2 天:2 第 3 天:3 第 4 天:1, 1提示:
1 <= D <= weights.length <= 500001 <= weights[i] <= 500
唯一一道没看题解就做出来的中等题,不过还是先看了下题解标题是二分法,就立马关掉题解自己写了,之前刚好看了二分法解有答案范围的题,真是很妙。————只要答案有范围,就可以二分法测试当前中点是否就是答案,难点就在于测试函数check()。
class Solution { public int shipWithinDays(int[] ws, int d) { //二分法,想要的答案x是[0,sum]之间的,sum是货物总重。 //关键在于如何判断船舶最大承受载重为x时,是否能在D天内运载完全部货物————直接货物一个一个加,不超过x就加,加到刚好不超过,这样货物分批运完看有没有D天即可,超过D就是false,否则true。 int sum = 0; int j = ws.length; for(int i = 0;i < j;i++){ sum+=ws[i]; } int left = 0,right = sum; while(left < right){ int medium = (left+right)/2; if(check(medium,ws,d,j)){ // System.out.println("YES"); right = medium; } else{ left = medium+1; } // System.out.println(medium); } return right; } boolean check(int x,int[] ws,int d,int len){ int temp = 0; int days = 1;//最后一天不管超没超都得+1,这里提前加好 for(int i = 0;i < len;i++){ if(ws[i] > x){//货物过大,直接false return false; } if(temp + ws[i] > x){ days++; temp = 0; } temp+=ws[i]; } return days <= d; } }效率也比较高,毕竟是O(nlogn)。
Top100
-
226. 翻转二叉树
难度简单
翻转一棵二叉树。
示例:
输入:
4 / \ 2 7 / \ / \ 1 3 6 9输出:
4 / \ 7 2 / \ / \ 9 6 3 1备注:
这个问题是受到 Max Howell 的 原问题 启发的 :谷歌:我们90%的工程师使用您编写的软件(Homebrew),但是您却无法在面试时在白板上写出翻转二叉树这道题,这太糟糕了。
/** * Definition for a binary tree node. * public class TreeNode { * int val; * TreeNode left; * TreeNode right; * TreeNode() {} * TreeNode(int val) { this.val = val; } * TreeNode(int val, TreeNode left, TreeNode right) { * this.val = val; * this.left = left; * this.right = right; * } * } */ class Solution { public TreeNode invertTree(TreeNode root) {//记得root始终是和node独立的。 if(root == null) return null; TreeNode node = new TreeNode(root.val); node.left = invertTree(root.right); node.right = invertTree(root.left); return node; } } -
难度简单
给定两个二叉树,想象当你将它们中的一个覆盖到另一个上时,两个二叉树的一些节点便会重叠。
你需要将他们合并为一个新的二叉树。合并的规则是如果两个节点重叠,那么将他们的值相加作为节点合并后的新值,否则不为 NULL 的节点将直接作为新二叉树的节点。
示例 1:
输入: Tree 1 Tree 2 1 2 / \ / \ 3 2 1 3 / \ \ 5 4 7 输出: 合并后的树: 3 / \ 4 5 / \ \ 5 4 7注意: 合并必须从两个树的根节点开始。
二叉树一律递归。递归的是节点,,返回的也是节点
/** * Definition for a binary tree node. * public class TreeNode { * int val; * TreeNode left; * TreeNode right; * TreeNode() {} * TreeNode(int val) { this.val = val; } * TreeNode(int val, TreeNode left, TreeNode right) { * this.val = val; * this.left = left; * this.right = right; * } * } */ class Solution { public TreeNode mergeTrees(TreeNode root1, TreeNode root2) { //二叉树一律递归。递归的是节点,,返回的也是节点。第四种情况是两棵树左/右孩子均为null,归纳到情况1中。 if(root1 == null){//情况1 return root2; } if(root2 == null){//情况2 return root1; } TreeNode merge = new TreeNode(root1.val + root2.val);//情况3 merge.left = mergeTrees(root1.left,root2.left); merge.right = mergeTrees(root1.right,root2.right); return merge; } } -
104. 二叉树的最大深度
难度简单
给定一个二叉树,找出其最大深度。
二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。
说明: 叶子节点是指没有子节点的节点。
示例:
给定二叉树[3,9,20,null,null,15,7],3 / \ 9 20 / \ 15 7返回它的最大深度 3 。
/** * Definition for a binary tree node. * public class TreeNode { * int val; * TreeNode left; * TreeNode right; * TreeNode() {} * TreeNode(int val) { this.val = val; } * TreeNode(int val, TreeNode left, TreeNode right) { * this.val = val; * this.left = left; * this.right = right; * } * } */ class Solution { int sum = 0; public int maxDepth(TreeNode root) { backtrack(root,0); return sum; } public void backtrack(TreeNode root,int now){ // System.out.println(now+"|"+sum); if(root == null){ sum = sum < now ? now : sum; return; } backtrack(root.left,now+1); backtrack(root.right,now+1); return; } } -
46. 全排列
难度中等1264收藏分享切换为英文接收动态反馈
给定一个 没有重复 数字的序列,返回其所有可能的全排列。
示例:
输入: [1,2,3] 输出: [ [1,2,3], [1,3,2], [2,1,3], [2,3,1], [3,1,2], [3,2,1] ]全排列的数字和字符串,用回溯。
class Solution { public List<List<Integer>> permute(int[] nums) { //全排列题-->回溯(操作,递归,撤销操作;类似于广度优先搜索) List<List<Integer>> result = new ArrayList<>(); backtrack(nums,result,new ArrayList<>(),0); return result; } public void backtrack(int[] nums,List<List<Integer>> result,List<Integer> now,int start){ if(now.size() == nums.length){ result.add(new ArrayList<>(now)); return; } for(int i = 0,j = nums.length;i < j;i++){ if(now.contains(nums[i])) continue; now.add(nums[i]); backtrack(nums,result,now,i+1); now.remove(now.size()-1); } } } -
94. 二叉树的中序遍历
难度中等
给定一个二叉树的根节点
root,返回它的 中序 遍历。/** * Definition for a binary tree node. * public class TreeNode { * int val; * TreeNode left; * TreeNode right; * TreeNode() {} * TreeNode(int val) { this.val = val; } * TreeNode(int val, TreeNode left, TreeNode right) { * this.val = val; * this.left = left; * this.right = right; * } * } */ class Solution { public List<Integer> inorderTraversal(TreeNode root) { List<Integer> result = new ArrayList<>(); backroll(root,result); return result; } public void backroll(TreeNode root,List<Integer> result){ if(root == null){ return; } backroll(root.left,result); result.add(root.val); backroll(root.right,result); } } -
406. 根据身高重建队列
难度中等
假设有打乱顺序的一群人站成一个队列,数组
people表示队列中一些人的属性(不一定按顺序)。每个people[i] = [hi, ki]表示第i个人的身高为hi,前面 正好 有ki个身高大于或等于hi的人。请你重新构造并返回输入数组
people所表示的队列。返回的队列应该格式化为数组queue,其中queue[j] = [hj, kj]是队列中第j个人的属性(queue[0]是排在队列前面的人)。示例 1:
输入:people = [[7,0],[4,4],[7,1],[5,0],[6,1],[5,2]] 输出:[[5,0],[7,0],[5,2],[6,1],[4,4],[7,1]] 解释: 编号为 0 的人身高为 5 ,没有身高更高或者相同的人排在他前面。 编号为 1 的人身高为 7 ,没有身高更高或者相同的人排在他前面。 编号为 2 的人身高为 5 ,有 2 个身高更高或者相同的人排在他前面,即编号为 0 和 1 的人。 编号为 3 的人身高为 6 ,有 1 个身高更高或者相同的人排在他前面,即编号为 1 的人。 编号为 4 的人身高为 4 ,有 4 个身高更高或者相同的人排在他前面,即编号为 0、1、2、3 的人。 编号为 5 的人身高为 7 ,有 1 个身高更高或者相同的人排在他前面,即编号为 1 的人。 因此 [[5,0],[7,0],[5,2],[6,1],[4,4],[7,1]] 是重新构造后的队列。示例 2:
输入:people = [[6,0],[5,0],[4,0],[3,2],[2,2],[1,4]] 输出:[[4,0],[5,0],[2,2],[3,2],[1,4],[6,0]]提示:
1 <= people.length <= 20000 <= hi <= 1060 <= ki < people.length- 题目数据确保队列可以被重建
//先根据hi升序排序,然后用ki降序排序,这样达到了局部最优解。然后根据ki作为下标插入结果数组里,遇到冲突就插在冲突的元素前面(LinkedList有一个add(index,element)方法刚好就是对应下标没有元素就插入该下标,有元素冲突了就插入到那个元素之前)。 class Solution { public int[][] reconstructQueue(int[][] people) { //贪心,局部最优->全局最优,只要没有反例即可解出答案。否则考虑动态规划。 Arrays.sort(people,new Comparator<int[]>(//局部排序的原理是先对[0]升序,再对[1]降序 ){ @Override public int compare(int[] person1,int[] person2){//返回正数,传入的参数就会正序排放 if(person1[0] == person2[0]){ return person1[1] - person2[1];//再对[1]降序 } else{ return person2[0] - person1[0];//先对[0]升序 } } }); //题解大佬的极简排序法 // Arrays.sort(people, (o1, o2) -> o1[0] == o2[0] ? o1[1] - o2[1] : o2[0] - o1[0]); LinkedList<int[]> result = new LinkedList<>(); for(int i = 0,j = people.length;i < j;i++){ result.add(people[i][1],people[i]); } return result.toArray(new int[result.size()][2]); } }注意:这题用到了Arrays.sort,这个静态方法一般用于int[]或int[][]排序,也可以用于T[]排序,但是两者比较流程不同:
对于自定义对象数组排序,首先需要这个对象继承Compare接口,重写compareTo方法,然后就可以直接用Arrays.sort方法对自定义对象数组排序,如:
class B implements Comparable{ @Override public int compareTo(Object o) { return 0; } } public class Test { public static void main(String[] args) { B[] bArr = new B[2]; Arrays.sort(bArr); } }对于int[][],无法对int这种基本数据类型进行重写比较方法,需要在Arrays.sort的参数上添加Comparetor接口并重写compare方法(题解即有)。
-
39. 组合总和
难度中等
给定一个无重复元素的数组
candidates和一个目标数target,找出candidates中所有可以使数字和为target的组合。candidates中的数字可以无限制重复被选取。说明:
- 所有数字(包括
target)都是正整数。 - 解集不能包含重复的组合。
示例 1:
输入:candidates = [2,3,6,7], target = 7, 所求解集为: [ [7], [2,2,3] ]示例 2:
输入:candidates = [2,3,5], target = 8, 所求解集为: [ [2,2,2,2], [2,3,3], [3,5] ]提示:
1 <= candidates.length <= 301 <= candidates[i] <= 200candidate中的每个元素都是独一无二的。1 <= target <= 500
这题是回溯的经典算法题。
//不知道为什么sum会出现不符合num数组总和的情况。 class Solution { public List<List<Integer>> combinationSum(int[] candidates, int target) { //回溯 List<List<Integer>> result = new ArrayList<>(); backroll(result,new ArrayList<Integer>(),candidates,target,0); return result; } public void backroll(List<List<Integer>> result,List<Integer> num,int[] candidates,int target,int sum){ if(sum == target){ //去掉重复的数组,如[2,2,3]和[2,3,2],方法是排序后插入,插入时排序后比较是否重复 System.out.println("排序前"+num); Collections.sort(num); System.out.println("排序后"+num); if(!result.contains(num)){ result.add(new ArrayList<>(num)); System.out.println(sum+" | "+num); } return; } if(sum > target){ return; } for(int i = 0,j = candidates.length;i < j;i++){ sum+=candidates[i]; num.add(candidates[i]); backroll(result,num,candidates,target,sum); sum-=candidates[i]; num.remove(num.size()-1); } } } //过的时候我还挺莫名其妙......去掉了1和4处,原因看2处。2处将i = 0修改为i = start(引入了start参数,这个参数一开始是0,然后是i,起到去重作用)。3处很有讲究,如果传入i+1就是得出不重复元素的子集。 class Solution { public List<List<Integer>> combinationSum(int[] candidates, int target) { //回溯 List<List<Integer>> result = new ArrayList<>(); backroll(result,new ArrayList<Integer>(),candidates,target,0,0); return result; } public void backroll(List<List<Integer>> result,List<Integer> num,int[] candidates,int target,int start,int sum){ if(sum == target){ //去掉重复的数组,如[2,2,3]和[2,3,2],方法是排序后插入,插入时排序后比较是否重复——这里不排序反而是对的。。。 // System.out.println("排序前"+num); // Collections.sort(num); // 1 // System.out.println("排序后"+num); //if(!result.contains(num)){ // 4 result.add(new ArrayList<>(num)); // System.out.println(sum+" | "+num); //} return; } if(sum > target){ return; } for(int i = start,j = candidates.length;i < j;i++){ // 2 sum+=candidates[i]; num.add(candidates[i]); backroll(result,num,candidates,target,i,sum); // 3 num.remove(num.size()-1); sum-=candidates[i]; } } } - 所有数字(包括
-
139. 单词拆分
难度中等
给定一个非空字符串 s 和一个包含非空单词的列表 wordDict,判定 s 是否可以被空格拆分为一个或多个在字典中出现的单词。
说明:
- 拆分时可以重复使用字典中的单词。
- 你可以假设字典中没有重复的单词。
示例 1:
输入: s = "leetcode", wordDict = ["leet", "code"] 输出: true 解释: 返回 true 因为 "leetcode" 可以被拆分成 "leet code"。示例 2:
输入: s = "applepenapple", wordDict = ["apple", "pen"] 输出: true 解释: 返回 true 因为 "applepenapple" 可以被拆分成 "apple pen apple"。 注意你可以重复使用字典中的单词。示例 3:
输入: s = "catsandog", wordDict = ["cats", "dog", "sand", "and", "cat"] 输出: false//时间超限,超限的那个例子故意给了原根字典里只有少数能匹配的字符(串),然后要匹配的字符串又特别长。 class Solution { boolean flag = false; public boolean wordBreak(String s, List<String> wordDict) { //回溯,每次做选择是从wordDict里做,直到可能的选择全部做完停止循环 int lens = s.length(); backroll(0,s,wordDict,lens); return flag; } void backroll(int start,String s, List<String> wordDict,int lens){ if(start == lens){ flag = true; return; } for(int i = 0;i < wordDict.size();i++){ int len = wordDict.get(i).length(); if(start+len > lens || !s.substring(start,start+len).equals(wordDict.get(i))){ continue; } start += len; backroll(start,s,wordDict,lens); start -= len; } } } //一开始以为哪里做的不对,改了下,还是不行,这才发现是例子的极端: class Solution { boolean flag = false; public boolean wordBreak(String s, List<String> wordDict) { //回溯,每次做选择是从wordDict里做,直到可能的选择全部做完停止循环 int lens = s.length(); backroll(0,s,wordDict,lens); return flag; } void backroll(int start,String s, List<String> wordDict,int lens){ if(start == lens){ flag = true; return; } for(String temp : wordDict){ int len = temp.length(); if(start+len > lens || !s.substring(start,start+len).equals(temp)){ continue; } start += len; backroll(start,s,wordDict,lens); start -= len; } } }超限的例子如下:
"acaaaaabbbdbcccdcdaadcdccacbcccabbbbcdaaaaaadb" ["abbcbda","cbdaaa","b","dadaaad","dccbbbc","dccadd","ccbdbc","bbca","bacbcdd","a","bacb","cbc","adc","c","cbdbcad","cdbab","db","abbcdbd","bcb","bbdab","aa","bcadb","bacbcb","ca","dbdabdb","ccd","acbb","bdc","acbccd","d","cccdcda","dcbd","cbccacd","ac","cca","aaddc","dccac","ccdc","bbbbcda","ba","adbcadb","dca","abd","bdbb","ddadbad","badb","ab","aaaaa","acba","abbb"]







 浙公网安备 33010602011771号
浙公网安备 33010602011771号