【软考】算法3-动态规划法

动态规划

动态规划法是考的最多的算法，最典型的是0-1背包，最长公共子序列，矩阵连乘

动态规划与分治法不同的是：动态规划法分解得到的子问题不是独立的。动态规划是全局最优解。

0-1背包问题

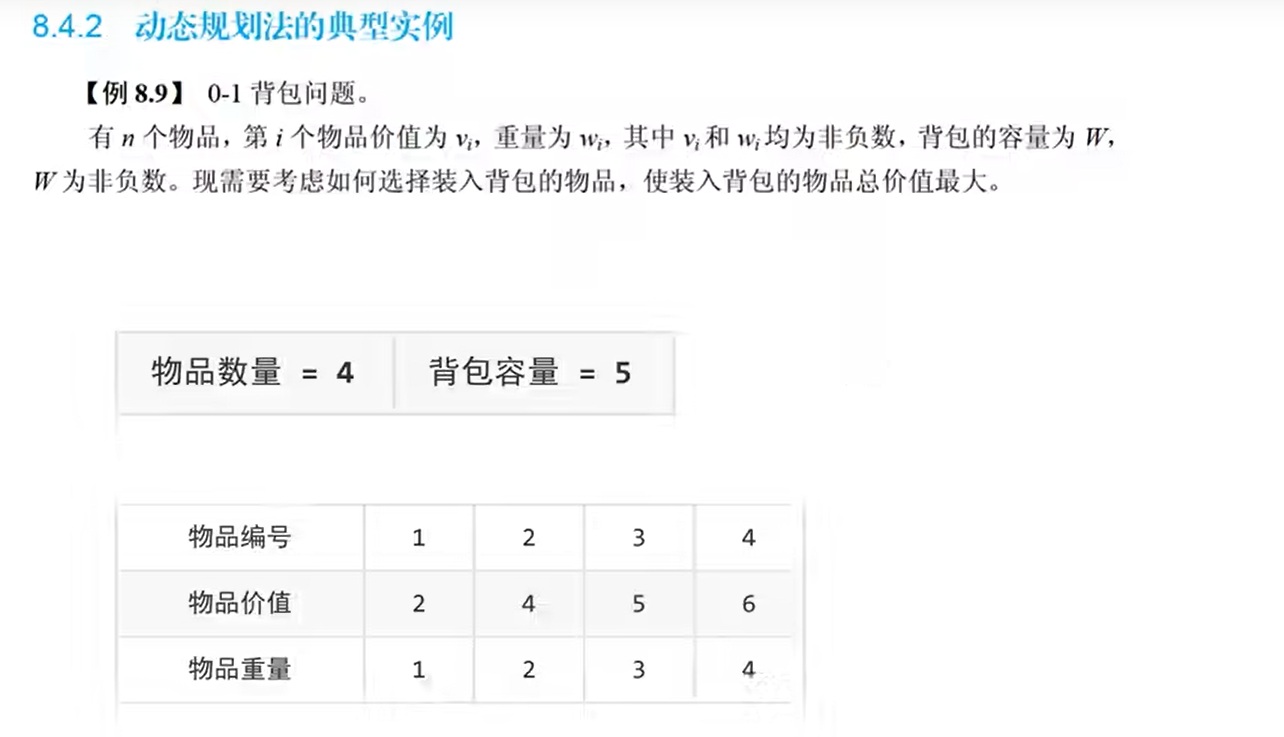
使用动态规划解决0-1背包问题。

用数组V[]来存价值，用W[]来存重量，然后考虑容量搭配问题，求得最优解。

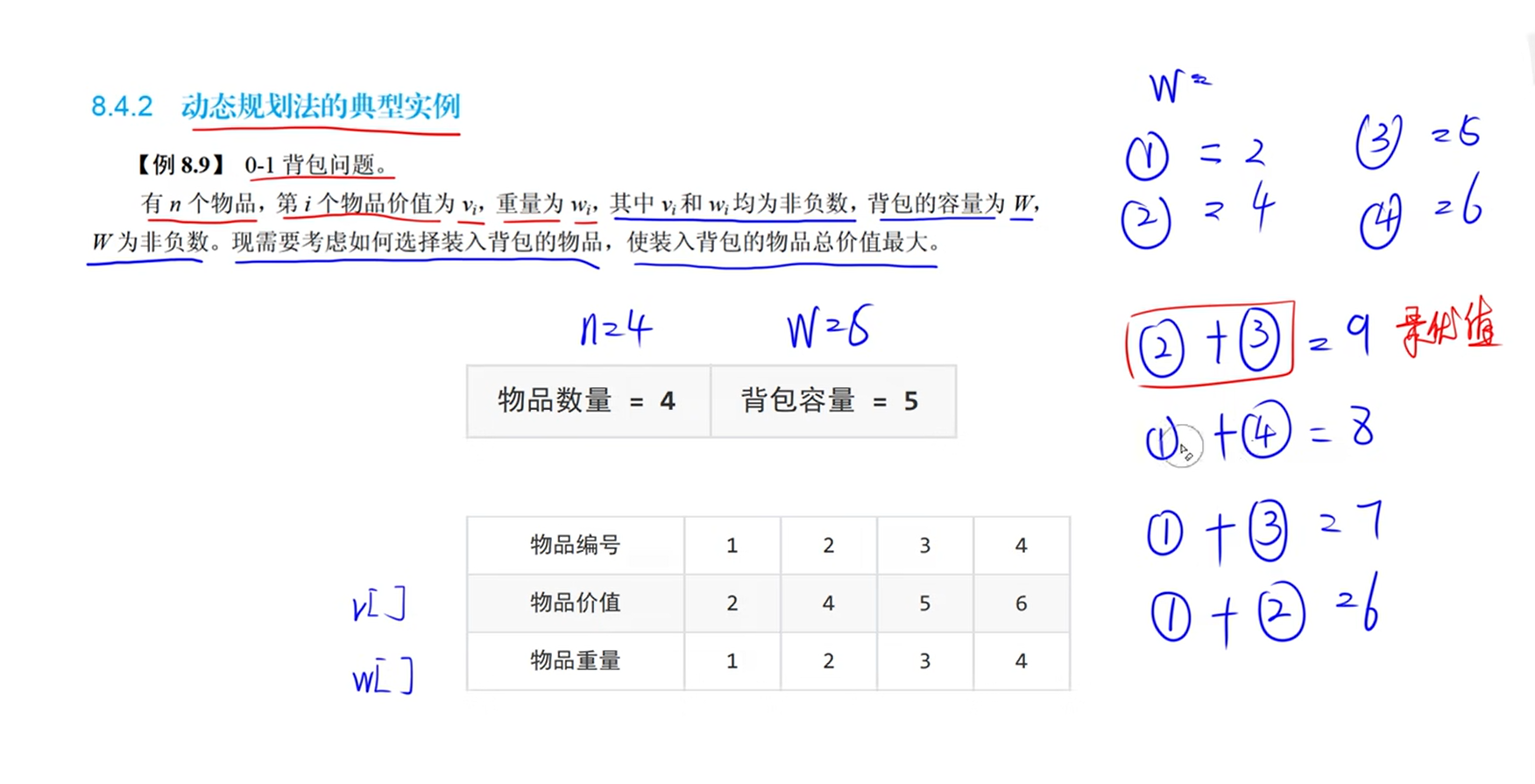
在有限的容量里，使价值最大。

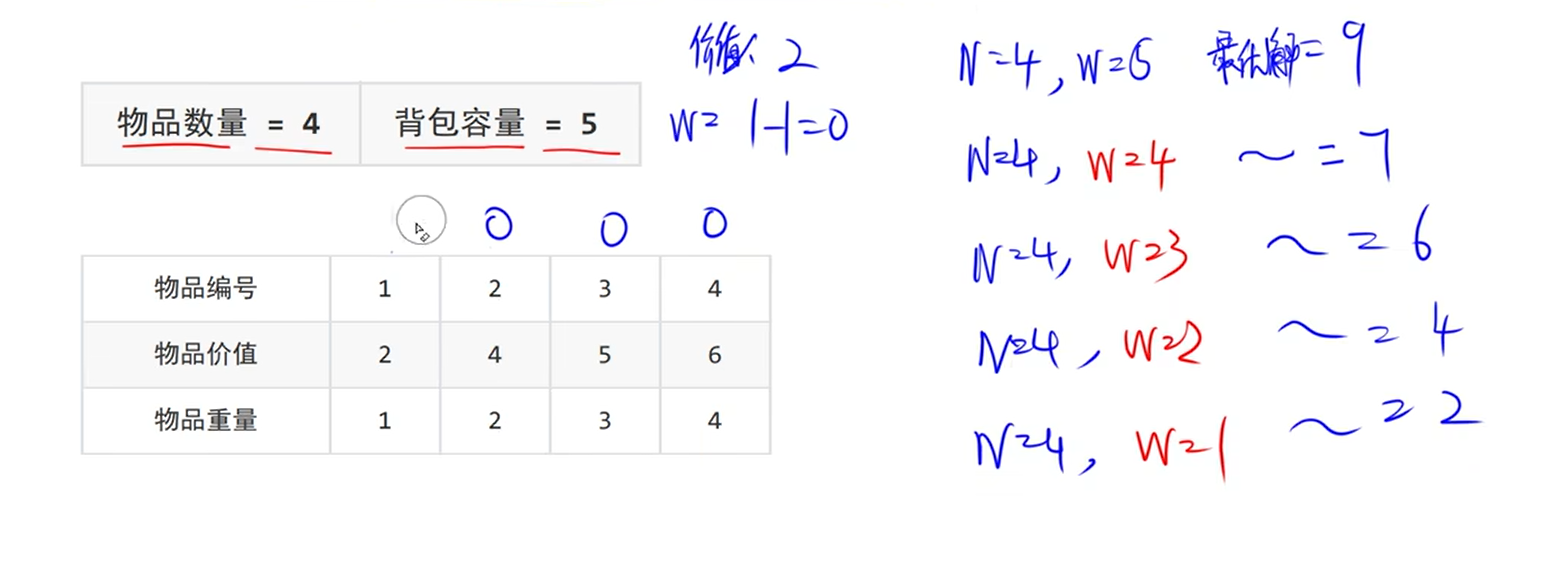
分解成子问题，比如W=5，W=4，...W=1的时候的情况。

也可以分解成：N=3，N=2，N=1的情况。

根据表格来做：

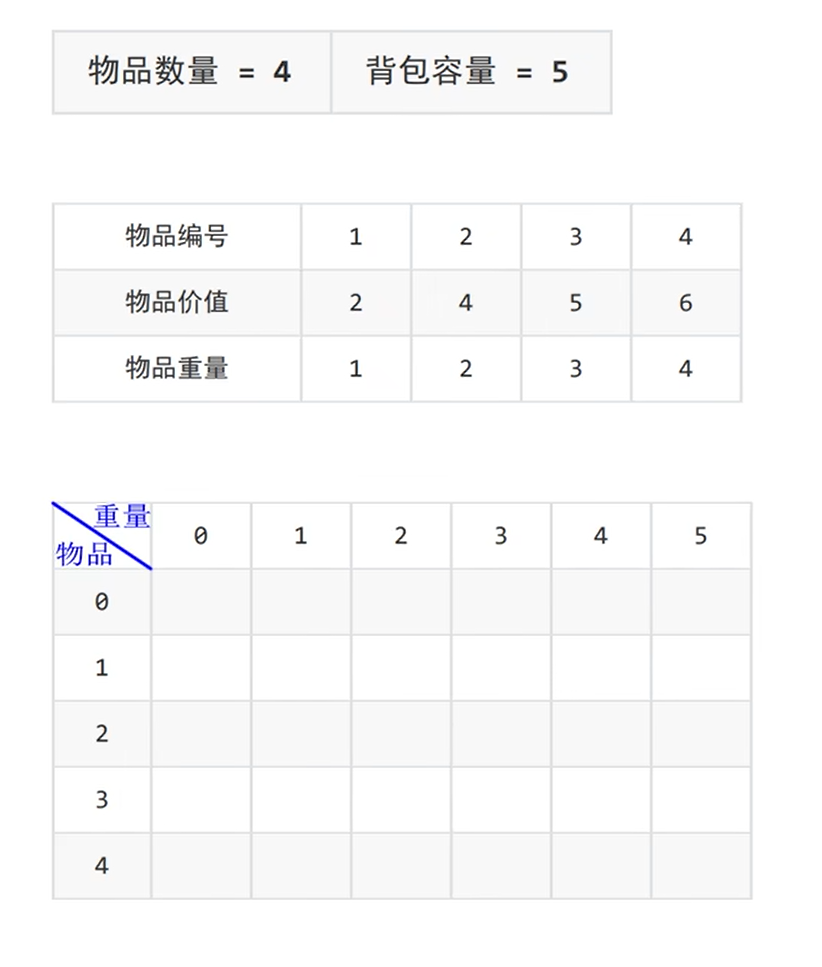
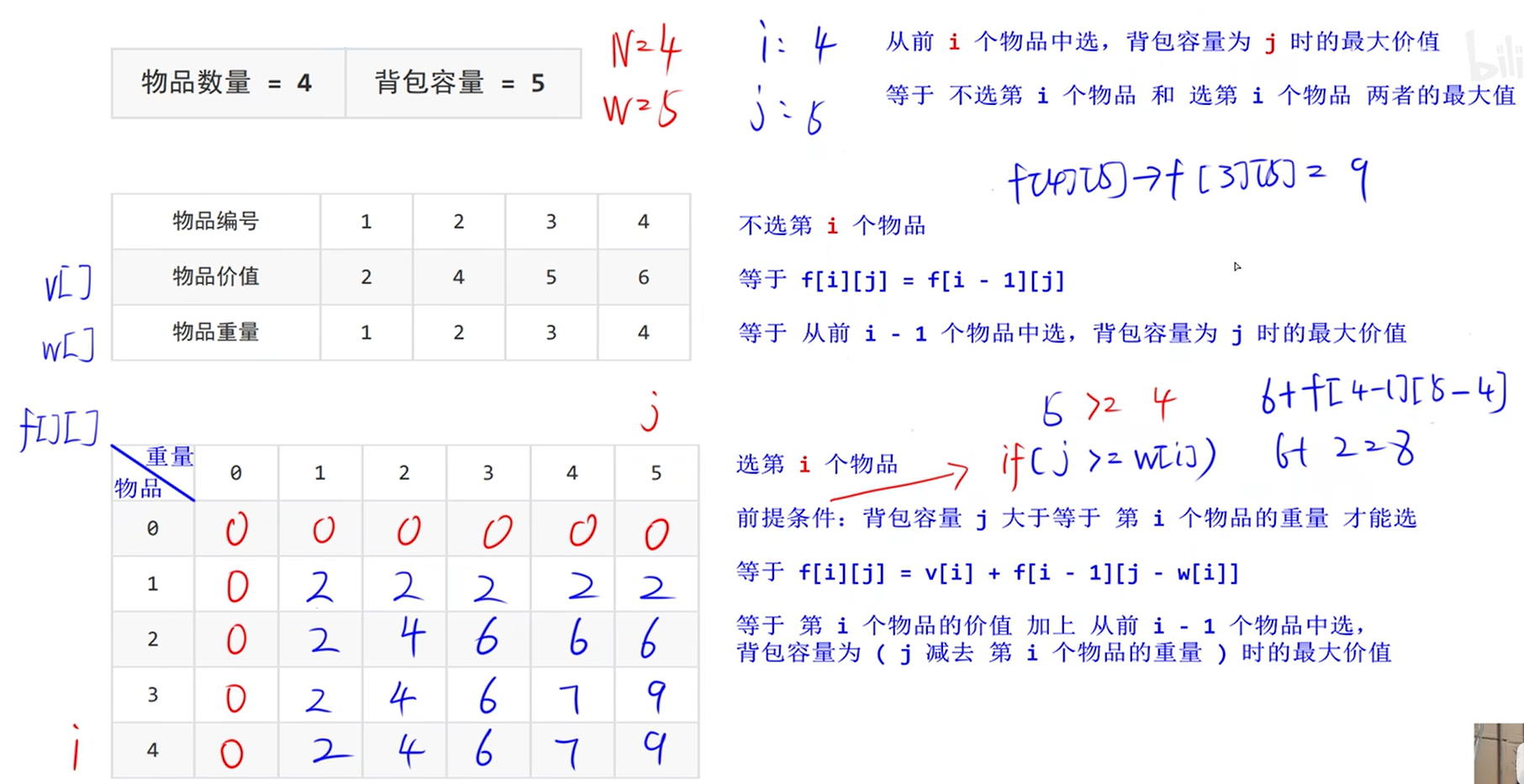
对于背包问题，要么不选，要么选，两种选择。

i是物品，j是背包容量。

不选第i个物品=从前第i-1个物品中选 = f[i] [j] == f[i-1] [j]，这个是代码形式。

选第i个物品，需要满足前提条件：有能装下这个物品的能力。if(j >= w[i])。

①其中j=w[i]表示恰好能装下第i个物品的能力。

②j >w[i]表示比第i个物品还多出一点容量。

i=0和j=0是边界。用数组V[]来存价值，用W[]来存重量，令问题为f[i] [j]，然后考虑容量搭配问题，求得最优解。

开始：

把问题分为j = w[i]和j > w[i]来讨论。有些时候只能满足j = w[i]，有些情况j >= w[i])，后者的情况提供两种选择余地，选或者是不选，此时比较不选第i个物品和选择第i个物品两者最大值。

1. i=1，j=1，即当前问题为f[1] [1]，f[1] [1]=f[0] [1]，从前1个物品中选。那么此时有两种选择：选，或者不选第i个物品。当前情况，只能选第一个物品。根据判断if(j > w[i])

​ 如果j=w[i]，恰好装下第1个物品，所以价值可以知道为2.

​ 如果j > w[i]，那也只能装物品1，所以价值为2.

2. i=2，j=3.那直接分情况：

​ 如果j=w[i]，那可以具有恰好装下第二个物品的容量，价值为4，但是这里j=3，所以还有空间。所以是j=3 > w[i]，能装第一个物品和第二个物品，价值为6，以此类推。

所以完成上面的图表。

可以总结出规律：当 j > w[i]，选中第i个物品之后，然后就从i-1中选出最有价值的物品，使得价值最大化。

比如f[2] [3]=4+f[i-1] [j-w[i]]=4+f[2-1] [3-2]

得出公式：f[i] [j] = v[i] + f[i-1] [j - w[i]]

---

前面有点乱，直接实操一次：

比如i=3，j=4。此时 j>=w[i]，分类讨论

①假如选择存入第i个商品，则f[3] [4] = v[3]+ f [3-1] [4-w[3]] = v[3] + f[2] [1]，然后分析f[2] [1]，所以这里就体现了递归的思想。

②假如选择不存入第i个商品。则f[3] [4] =f[2] [4]，也就是从i-1开始算了。

然后比较①和②谁的价值最高，然后输出最终结果。

---

可以结合上面的思路写出代码：

1. 首先定义数组：

#define N 4；
#define W 5；
int main(){
	int v[] = {0,2,4,5,6};//物品价值数组
	int w[] = {0,1,2,3,4};//物品重量数组	
	int f[N+1][W+1] = {};//子问题解数组
	
	int i,j;
	//用两个for循环来完成上面的表格遍历，也即各种f的解决方案
	for(i = 1;i<=N;i++){
		for(j = 1;j<=W;j++){
			/*在循环里面，讨论两种情况：选第i个物品和不选第i个物品*/
			if(j>=W[i]){//选第i个物品的前提条件
				f[i][j] = max{f[i-1][j],v[i]+f[i-1][j-w[i]]};//在上面的两种情况中选择价值最大的
			}else{
				f[i][j] = f[i-1][j];//不选第i个物品
			}
		}
	}
	printf("%d\n",f[N][W])；//输出原问题的解
	for(i = 1;i<=N;i++){
		for(j = 1;j<=W;j++){
			printf("%d\n",f[i][j])；//打印子问题的解
		}
	}
}

接下来就写max函数判断大小了：

int max(int a.int b){
	return a>b?a:b
}

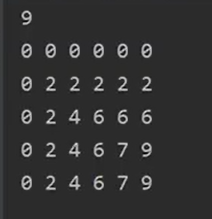
0-1背包时间/空间复杂度

时间复杂度：如果有两个嵌套for循环，时间复杂度是外层循环执行次数*内层循环执行次数，所以背包问题时间复杂度为：

O(N * w)

空间复杂度：也是一样的。O(N * w)

题型

2019年下半年

一般都是结合题型分析来进行在for和if里面判断挖空，以及函数体里面。太难了就放弃吧。