【软考】算法1-回溯法

序言

学习视频：https://www.bilibili.com/video/BV1uZ4y1y77y?p=1

算法题放到最后做，总共四个空，一般能拿到一般分已经可以了。代码部分能拿两个空，以及说出是什么类型得算法一个拿一个空。

关于时间复杂度的话，一般递归是看for循环，几个for循环则为几，如果不是递归，具体问题具体分析，要么是n，要么是nlgn。

一般来说，下午题基本都是四种算法之一：

（1）代码填空。4-5空，一空两分。

（2）时间/空间复杂度。/是什么算法。

（3）扩展。给一组数据，代入算法，求解。

回溯法（考过两次（截至2022年上半年之前））

经典例子：n皇后问题

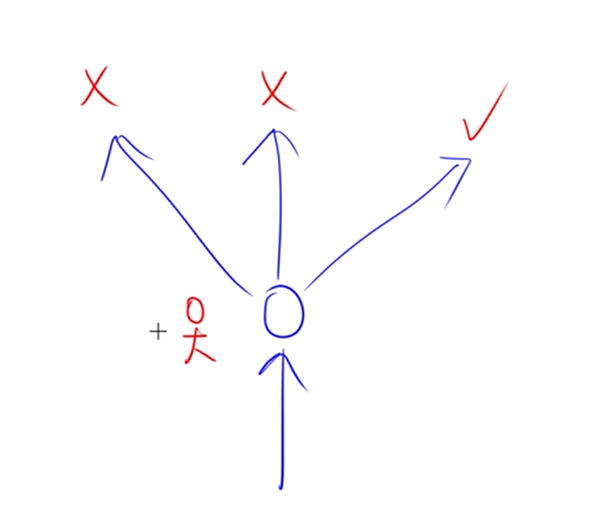
遇到错误的路就返回，即回溯。一条条路去试。

N皇后问题

非递归

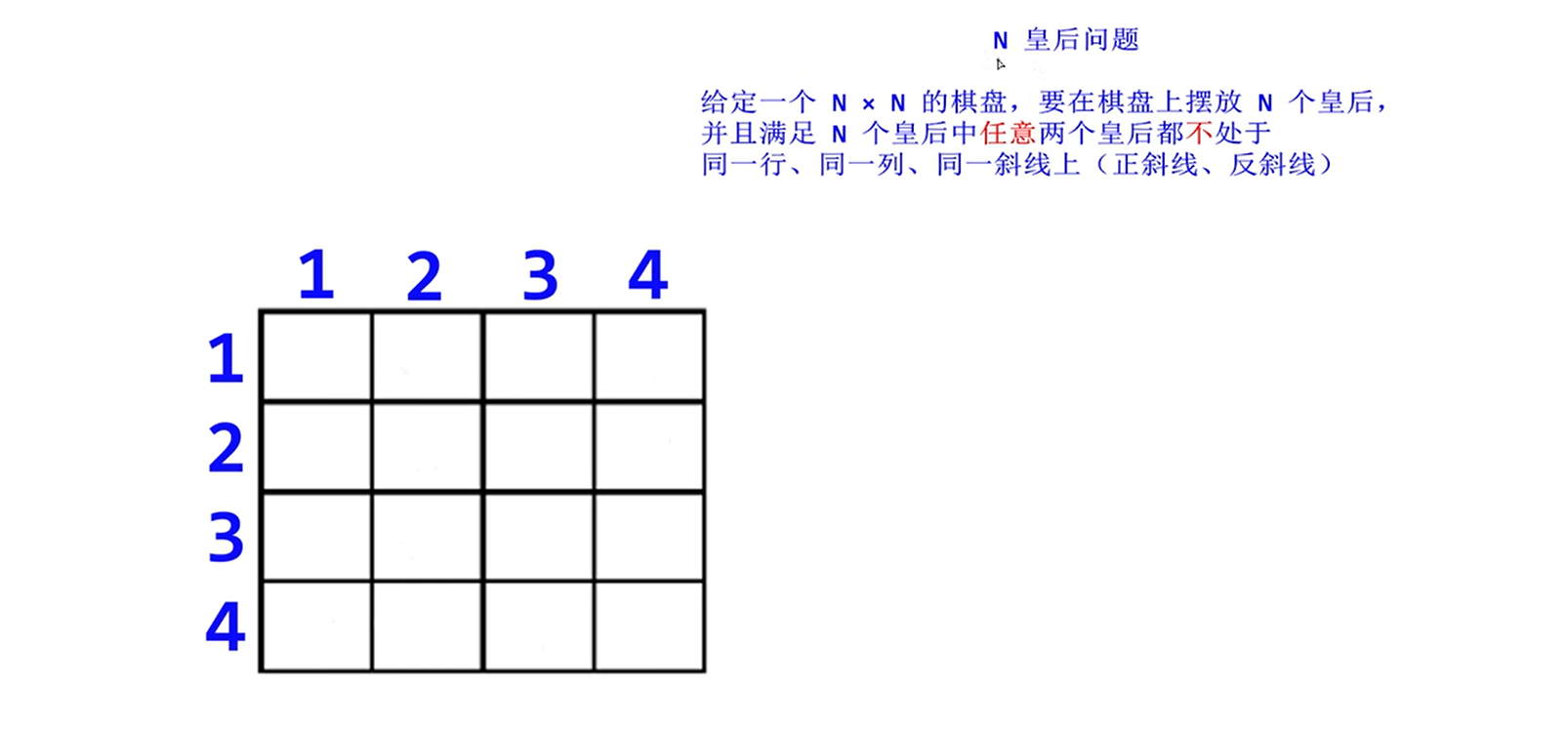
这里N=4。按行摆放皇后，摆完第一行后，然后跳到下一行一列列去试。

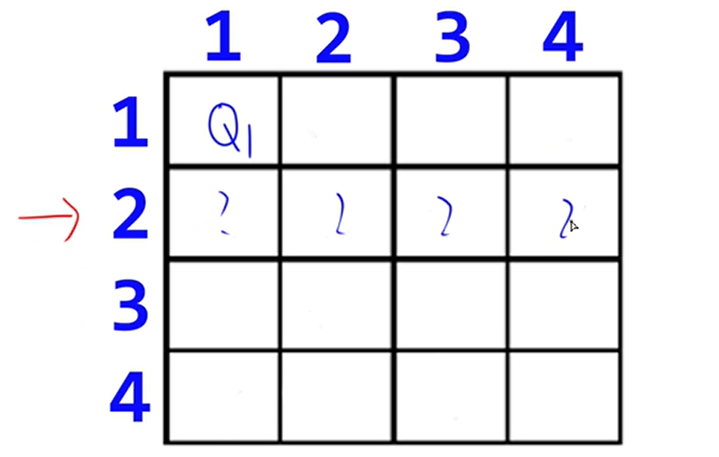
然后以此类推。具体的看视频：https://www.bilibili.com/video/BV1uZ4y1y77y?p=3

可以看到。比如第一行放Q1，第二行然后也安排一个Q2在（2，2），但是第三行皇后没有办法存放了，这时候就需要回溯到第二行重新摆放Q2，然后继续第三行第四行，如果在下面行仍然没有办法摆放，就一直回溯到能解决问题的行数为止，哪怕是第一行。

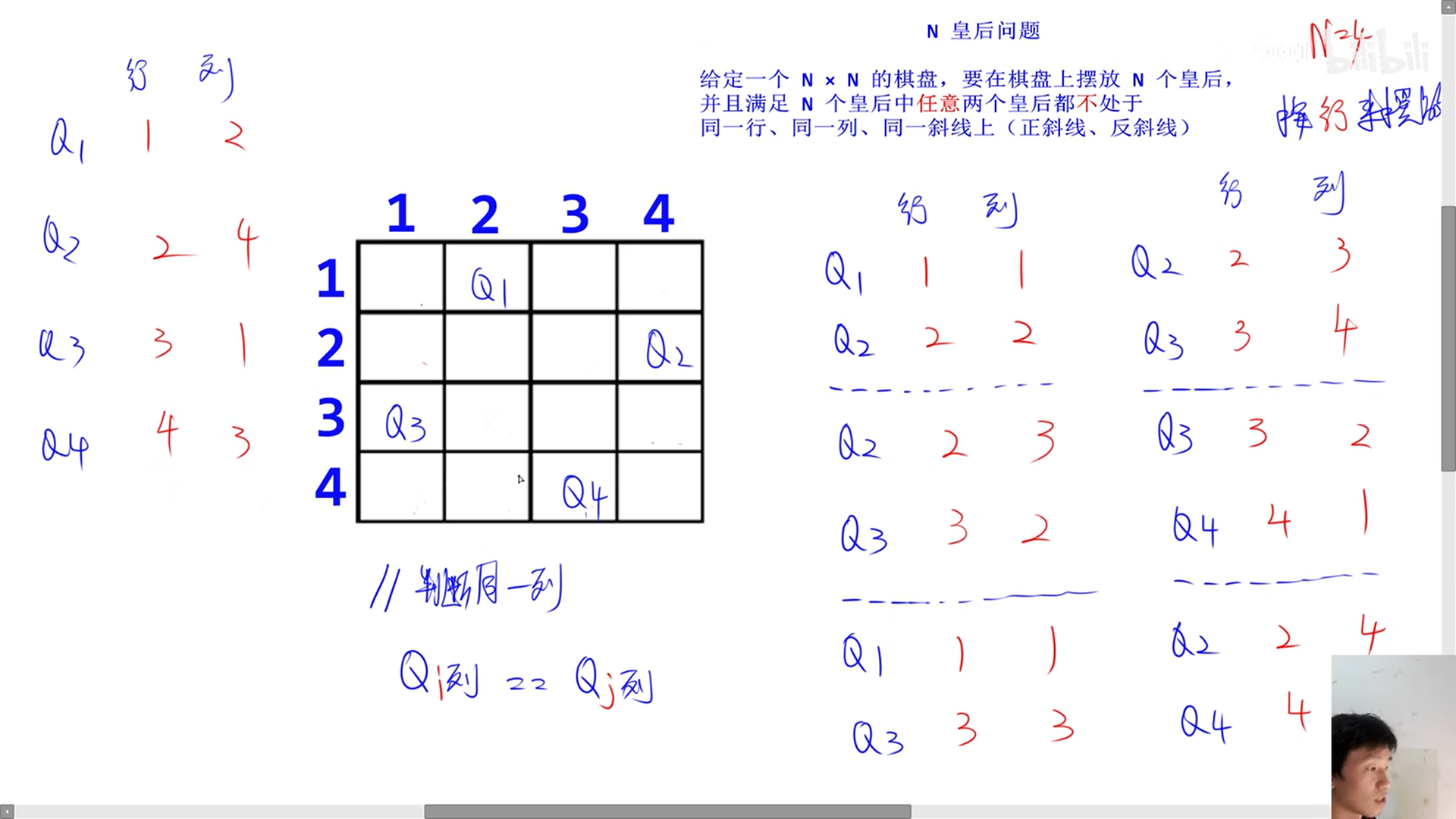
然后找到一组解，而软考里面一般表示列数：2，4，1，3

①判断是否在同一列：Qi列 == Qj列？？

②判断是否同一斜线：

观察规律可得，如果是斜线的，两颗皇后【行数之间的差值==列数之间的差值】，表示为：

abs【Qi行-Qi行】 == abs【Qi列-Qi列】

一、非递归（循环迭代）解决N皇后问题

1. 令i和j作为行数，【Q[i]和Q[j]】作为列数，C 语言中return 0 为假，检查代码为：

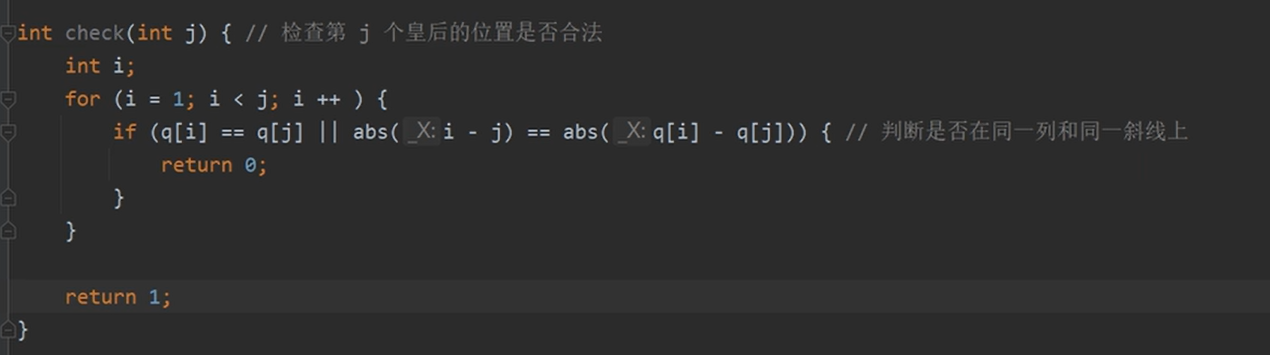
根据上面两个判断，如果return 0，即表示为假，如return 1，则表示为真。

2. 写皇后棋子摆放的方法：

一开始

int i;
for(i = 1;i<=N;i++){
	q[i]=0;
}

一开始对q[i]赋值为0，就是说明它们一开始还没有摆放在棋盘上。也就是把数组中的下标为0的地方，放初始值，这时候还没有摆上棋盘，棋盘是从数组的1开始的，到数组的5，中间就有4个位置了。

int answer = 0;//定义一个方案数，现在现别理他。

int j = 1;//表示正在摆放第j个皇后
while(j>=1){//待会儿解释j>=1
	q[j]=q[j]+1;//让棋子上棋盘，第j个皇后往后移一位。
	if(!check(j);){//判断是否合法
	q[j] = q[j]+1;
	}	
}

q[j]=q[j]+1;是因为初始值为0，这一步是上棋子端上棋盘，开始试探。

!check(j);是取反，当检查不合法，check返回0，那么if就要执行语句，所以把check进行取反，然后就让皇后的位置后移一位。

但是上面的if明显还不够，我们需要让棋子在不合法的时候一直挪，直到到棋盘的尽头。改进如下：

int j = 1;//表示正在摆放第j个皇后
while(j>=1){//待会儿解释j>=1
	q[j]=q[j]+1;//让棋子上棋盘，第j个皇后往后移一位。	
	   while(q[j]<=N &&!check(j)){	//不超出棋盘的边界，以及检查是否合法
	     q[j] = q[j]+1;
	}	
}

这时候要考虑外层while跳出循环的条件了：

①当棋子摆放的范围是不合理的，则这个后挪的操作就停止。

②当棋子摆放的范围合理，经过check方法检查也合理的，就停止循环。

可以用if语句来判断：

if(q[j]<=N){//表示第j个皇后没有超出边界
	
}else{//表示第j个皇后超出边界
	
}

if(q[j]<=N){//表示第j个皇后没有超出边界
	if(j == N){//找到一组皇后摆放方法的解
		answer = answer + 1；//方案就+1
		printf("方案&d",answer);
		for(i=1;i<=N;i++){//打印皇后
			printf("%d",q[i]);
		}
		printf("\n");
	}else{//还需要摆放下一个皇后
		j = j+1;
	}
}else{//表示第j个皇后超出边界
	j=j-1;
}

在棋子没有超出边界的时候，进行判断，判断有没有完成一组解。

j == N，其中j表示第n个皇后了，都已经摆到最后一个皇后了，那肯定完成了一种方法，那么就可以打印这种方法了，如果还没到N，那说明还没有到最后一个皇后，就需要继续打印。

如果棋子超出了边界，那证明当前没有更好的摆放选择，就需要回溯，所以j=j-1。

那么queen这个整体代码为：

void queen(){//求解N皇后方案
  int i;
  for(i = 1;i<=N;i++){
	q[i]=0;//初始化，不让棋子上桌
  }
  int answer = 0;//定义一个方案数
  int j = 1;//表示正在摆放第j个皇后
  /*从这里就开始让棋子上桌了*/
    while(j>=1){//开始让棋子上桌
	    q[j]=q[j]+1;//让棋子上棋盘，第j个皇后往后移一位。	
	    while(q[j]<=N &&!check(j)){	//不超出棋盘的边界，以及检查是否合法
	     q[j] = q[j]+1;
	     }	
	     /*上面的while就是让棋子进行试探，下面的if判断语句就是判断什么时候可以结束，要么找到了一组解，要么
	     *没有找到，回溯j-1*/
	    if(q[j]<=N){//表示第j个皇后没有超出边界
	         if(j == N){//找到一组皇后摆放方法的解
		     answer = answer + 1；//方案就+1
		     printf("方案&d",answer);
		     for(i=1;i<=N;i++){//打印皇后
			   printf("%d",q[i]);
		     }
		       printf("\n");
	     }else{//还需要摆放下一个皇后
		         j = j+1;
	          }
    }else{//表示第j个皇后超出边界
	        j=j-1;
         }
    }
}

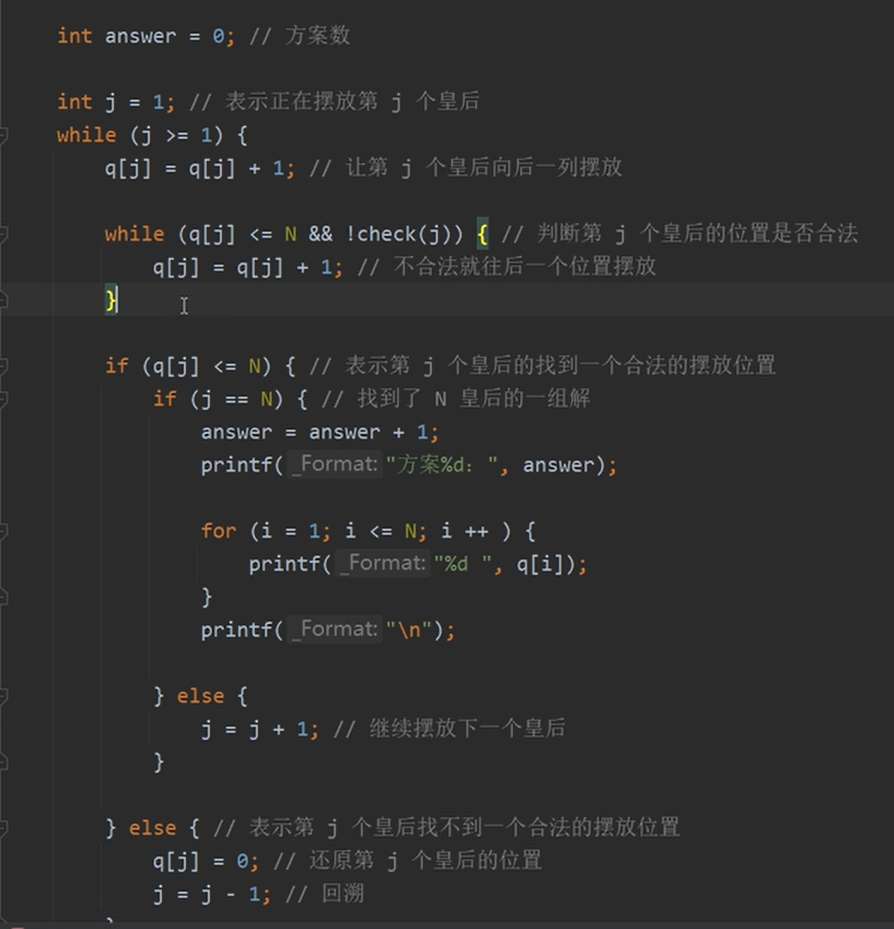
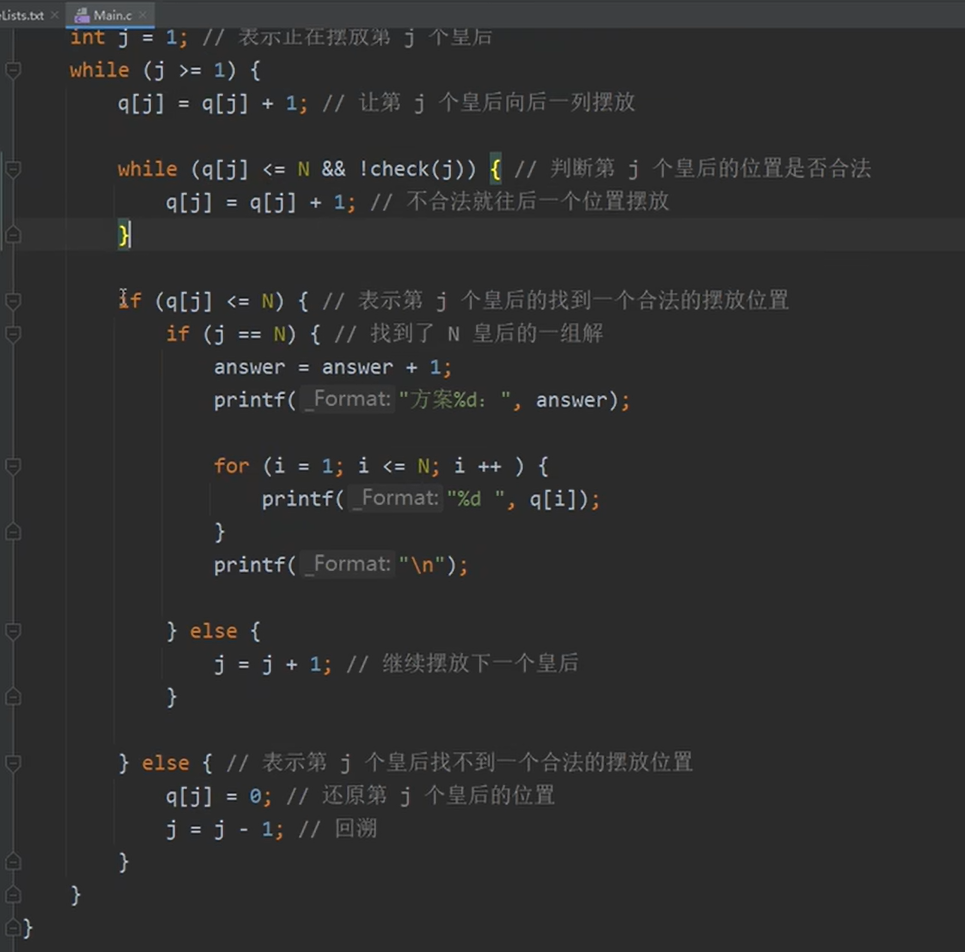
可以做出来2015年上半年的题目了。明白大致的挖空点就可以了。

递归

这里改变皇后棋子摆放的方法即可：

如果check为0，就不会进入if循环里面了，继续让皇后挪位（q[j] =i就是挪位的意思）如果check位真，就进入了if判断语句里面，就需要判断什么时候跳出循环了，如果j是最后一个就输出方案，如果j不是最后一个就摆放下一个皇后，而这里的回溯是通过递归来实现的。

只要记住挖空的点就好了，其它的感觉有点难理解。

可以做出来2019年上半年的题目了。

挖空的地方一般是if判断语句以及执行体内XXX+1这种。