数据结构与算法——图形结构(七)
数据结构——图
1、图的基本概念
2、图的数据表示法
2.1 邻接矩阵表示法
假设一个图A有n个顶点,我们以n*n的二维矩阵列来表示它,这个二维矩阵就是该图的邻接矩阵,此矩阵的定义如下:对于一个图G=(V,E),假设有n个顶点,n>=1,则可以将n个顶点的图使用一个n*n的二维矩阵来表示,其中A(i,j)=1,则表示图中有一条边(Vi,Vj)存在,反之,A(i,j)=0,则不存在(Vi,Vj)。
相关特性说明如下:
(1)对无向图而言,邻接矩阵一定是对称的,而对角线一定为0。有向图则不一定如此。
(2)在无向图中,任意结点 i 的度数就是第 i 行所有元素的和。在有向图中,结点 i 的出度就是第 i 行所有元素之和;结点 j 的入度就是第 j 列所有元素之和。
(3)用邻接矩阵法表示图共需要 n^2 个单位空间,由于无向图的邻接矩阵具有对称关系的,扣除对角线全部为 0 外,仅需要存储上三角形数据即可,因此仅需要n(n-1)/2。
接下来,我们看一个实际的例子,以邻接矩阵来表示无向图,无向图如下图所示:
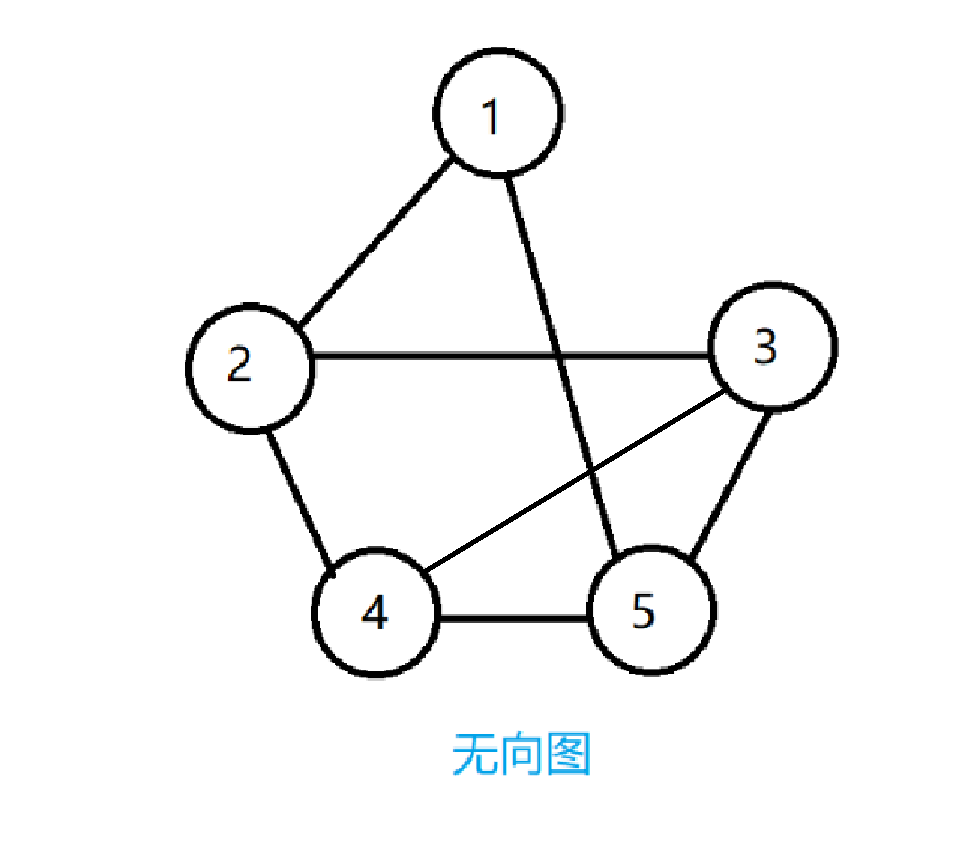
该无向图的邻接矩阵表示为:

我们接下来使用程序来创建邻接矩阵表示这个无向图,该程序使用Python2实现:
1 import numpy as np 2 3 #返回某个顶点在顶点列表中的位置索引 4 def find_index(node, node_list): 5 for i in range(len(node_list)): 6 if node == node_list[i]: 7 return i 8 return -1 9 10 #无向图的输入,采用二维数组 11 data = [[1, 2], [1, 5], [2, 3], [2, 4], [3, 4], [3, 5],[4, 5]] 12 #顶点列表 13 vertex_list = [1, 2, 3, 4, 5] 14 #创建一个邻接矩阵 15 Adj_matrix = np.zeros((5, 5), dtype=int) 16 #开始遍历图数据,生成邻接矩阵。 17 for i in range(len(data)): 18 temp1 = find_index(data[i][0], vertex_list) #找到顶点在顶点列表中的索引 19 temp2 = find_index(data[i][1], vertex_list) 20 Adj_matrix[temp1][temp2] = 1 #将有边的点出填入1 21 Adj_matrix[temp2][temp1] = 1 # 将有边的点出填入1 22 #输出邻接矩阵 23 for i in range(len(Adj_matrix)): 24 for j in range(len(Adj_matrix[0])): 25 print Adj_matrix[i][j], #python2的用法,在后面加“,”表示不换行。 26 print ""
运行的结果如下:
0 1 0 0 1
1 0 1 1 0
0 1 0 1 1
0 1 1 0 1
1 0 1 1 0
下面我们再看一个有向图的例子,以邻接矩阵来表示有向图,有向图如下图所示:

该有向图的邻接矩阵表示为:
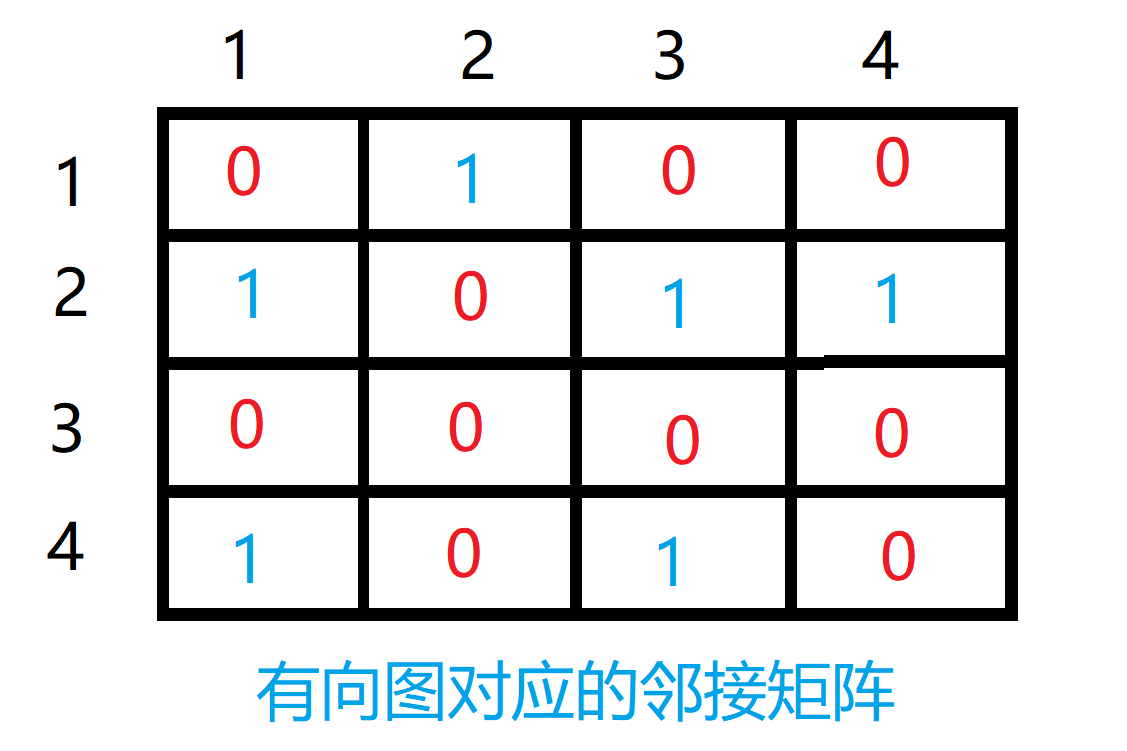
我们接下来使用程序来创建邻接矩阵表示这个有向图,该程序使用Python2实现:
1 import numpy as np 2 3 #返回某个顶点在顶点列表中的位置索引 4 def find_index(node, node_list): 5 for i in range(len(node_list)): 6 if node == node_list[i]: 7 return i 8 return -1 9 10 #有向图的输入,采用二维数组 11 data = [[1, 2], [2, 1], [2, 3], [2, 4], [4, 3], [4, 1]] 12 #顶点列表 13 vertex_list = [1, 2, 3, 4] 14 #创建一个邻接矩阵 15 Adj_matrix = np.zeros((5, 5), dtype=int) 16 #开始遍历数据,生成邻接矩阵。 17 for i in range(len(data)): 18 temp1 = find_index(data[i][0], vertex_list) #找到顶点在顶点列表中的索引 19 temp2 = find_index(data[i][1], vertex_list) 20 Adj_matrix[temp1][temp2] = 1 #将有边的点出填入1 21 #输出邻接矩阵 22 for i in range(len(Adj_matrix)): 23 for j in range(len(Adj_matrix[0])): 24 print Adj_matrix[i][j], #python2的用法,在后面加“,”表示不换行。 25 print ""
运行的结果如下:
0 1 0 0 0
1 0 1 1 0
0 0 0 0 0
1 0 1 0 0
0 0 0 0 0
2.2 邻接表法
前面所介绍的邻接矩阵法,优点是凭借着矩阵的运算又许多特别的应用。要在图中加入新边时,这个表示法的插入和删除相当简易。不过还要考虑到稀疏矩阵空间的浪费问题,另外,如果要计算所有顶点的度,其时间复杂度为O(n^2)。
因此可以考虑更有效的方法,就是邻接表法(Adjacency List)。这种表示法就是将一个n行的邻接矩阵表示成n个链表,这种做法和邻接矩阵相比较节省空间,如计算所有顶点的度时,其时间复杂度为O(n+e),缺点是:例如有新边加入图中或者从图中删除边时,就要修改相关的链接,较为麻烦费时。
首先,将图的n个顶点作为n个链表头,每个链表中的结点表示它们和链表头结点之间有边相连。每个结点的数据结构如下:
1 class list_node(object): #定义一个结点类 2 def __init__(self): #构造函数 3 self.data = 0 #结点的数据域 4 self.next = None #结点的指针域
在无向图中,因为对称关系,若有n个顶点、m个边,则形成n个链表头,2m个结点。若在有向图中,则有n个链表头以及m个结点,因此在邻接表中,求所有顶点的度所需的时间复杂度为O(n+m)。
接下来,我们看一个实际的例子,以邻接表来表示无向图,无向图如下图所示:

首先根据上图可知,因为5个顶点使用5个链表头,V1链表代表顶点1,与顶点1相邻的是顶点2和顶点5,以此类推,该无向图邻接表表示如下:
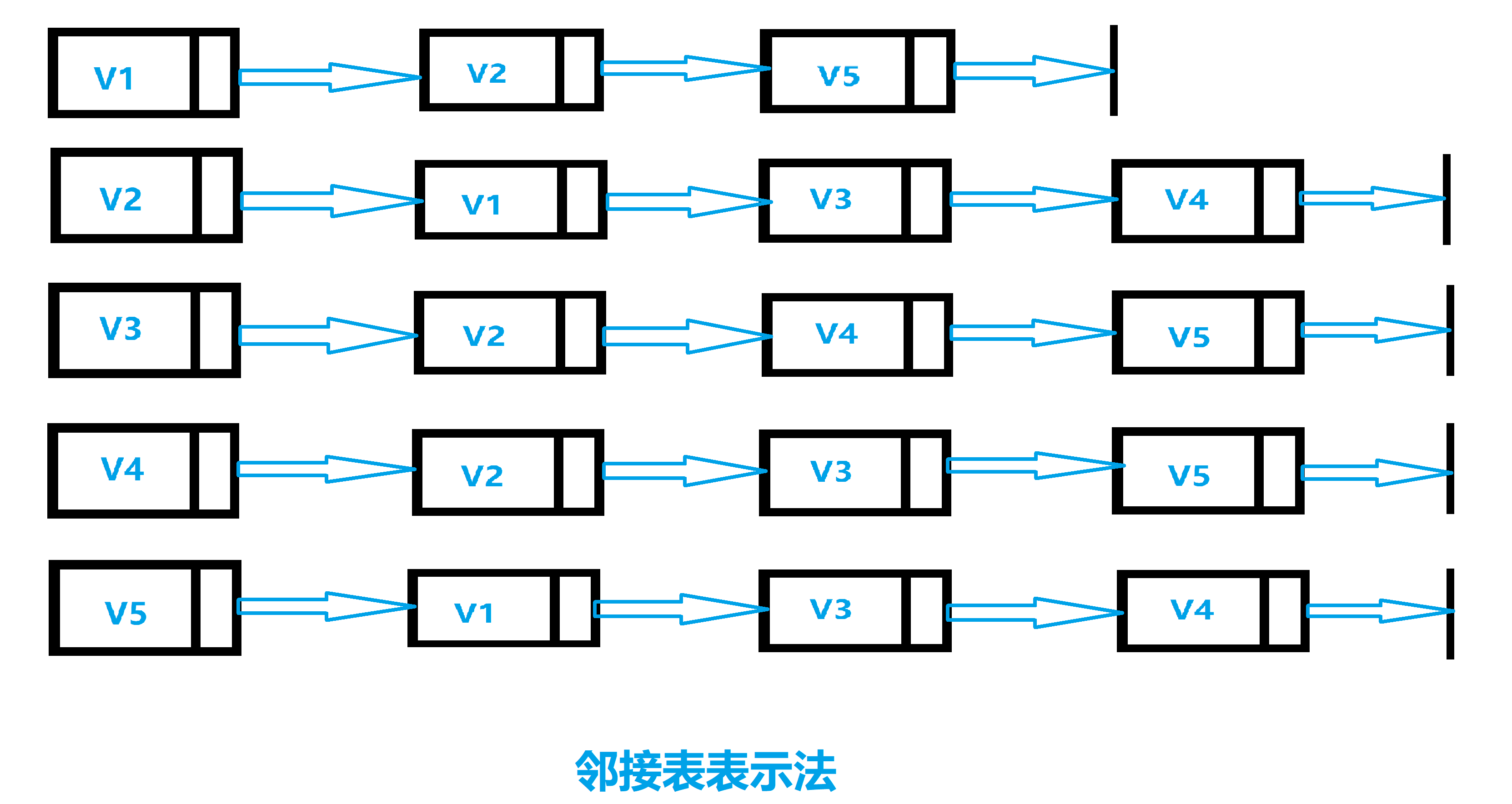
我们接下来使用程序来创建邻接矩阵表示这个有向图,该程序使用Python2实现:
1 class list_node(object): #定义一个结点类 2 def __init__(self): #构造函数 3 self.data = 0 #结点的数据域 4 self.next = None #结点的指针域 5 6 #顶点列表 7 vertex_list = [1, 2, 3, 4, 5] 8 head = [list_node] * len(vertex_list) #声明一个结点类型的列表 9 newnode = list_node() 10 data = [[1, 2], [2, 1], [1, 5], [5, 1], [2, 3], [3, 2], [2, 4], [4, 2], [3, 4], [4, 3], [3, 5], [5, 3], [4, 5], [5, 4]] 11 print len(data) 12 print "图的邻接表的内容" 13 print "-----------------------------------------------------" 14 15 for i in range(len(vertex_list)): #生成头结点,以五个顶点作为头结点 16 head[i].data = vertex_list[i] #分别将顶点列表的各个顶点元素存入头结点的数据域中 17 head[i].next = None #头结点指针域指向None 18 print "顶点 %d =>" % vertex_list[i], #打印头结点信息 19 for j in range(len(data)): #遍历整个传入的图的数据,通过它创建图的邻接链表结构 20 if data[j][0] == vertex_list[i]: #输入数据中的起始结点等于顶点,就在终止结点加入到该顶点的邻接链表中去。 21 newnode.data = data[j][1] #为终止顶点创建一个结点信息,并将其元素值加入到数据域中 22 newnode.next = head[i].next #采用头部插入的方式,插入该结点 23 head[i].next = newnode #这是头部插入法 24 print "[%d] " %newnode.data, #循环打印属于某一头结点邻接结点的所有数据元素。 25 print "" #表示换行
运行结果如下:
-----------------------------------------------------
顶点 1 => [2] [5]
顶点 2 => [1] [3] [4]
顶点 3 => [2] [4] [5]
顶点 4 => [2] [3] [5]
顶点 5 => [1] [3] [4]
2.3 图的特殊表示法(利用python的基本数据结构类型)
图是一种重要的数据结构,它可以代表各种结构和系统,从运输网络到通信网络,从细胞核中的蛋白质相互作用到人类在线交互。图是由顶点的有穷非空集合和顶点之间边的集合组成,通常表示为:G(V,E),其中,G表示一个图,V是图G中的顶点的集合,E是图G中边的集合。如下图:
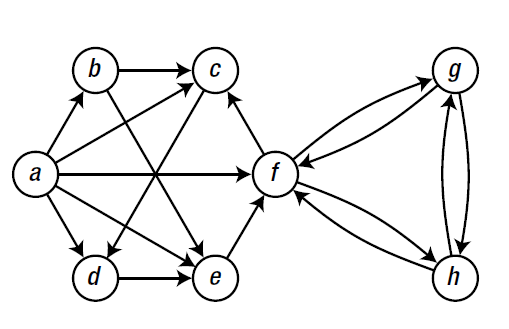
对于图结构的实现来说,最直观的方式之一就是使用邻接表来表示。基本上就是针对每一个节点设置一个邻接表,而对于邻接表的实现方式可以不同,针对python的特点以及内置的数据结构,可以使用列表、集合和字典来实现。
(1)邻接集合
第一种实现邻接表的方式是:针对每个结点设置一个邻居集合,在python中就是set。
1 a, b, c, d, e, f, g, h = range(8) 2 Adj_set = [ 3 {b, c, d, e, f}, 4 {c, e}, 5 {d}, 6 {e}, 7 {f}, 8 {c, g, h}, 9 {f, h}, 10 {f, g} 11 ] 12 #列表中的每个集合是每个结点的邻接点集 13 14 print b in Adj_set[a] #结点b是否是结点a的邻居结点 15 print len(Adj_set[a]) #结点a的出度
运行结果如下:
True
5
(2)邻接列表
第二种实现邻接表的方式是:针对每个结点设置一个邻居列表,在python中就是list。
1 a, b, c, d, e, f, g, h = range(8) 2 Adj_list = [ 3 [b, c, d, e, f], 4 [c, e], 5 [d], 6 [e], 7 [f], 8 [c, g, h], 9 [f, h], 10 [f, g] 11 ] 12 13 print b in Adj_list[a] #结点b是否是结点a的邻居结点 14 print len(Adj_list[a]) #结点a的出度
运行结果如下:
True
5
(3)加权的邻接字典
使用字典类型来代替集合或列表来表示邻接表。在字典类型中,每个邻居节点都会有一个键和一个额外的值,用于表示与其邻居节点(或出边)之间的关联性,如边的权重。
1 a, b, c, d, e, f, g, h = range(8) 2 Adj_dict_weight = [ 3 {b: 2, c: 1, d: 3, e: 9, f: 4}, 4 {c: 4, e: 3}, 5 {d: 8}, 6 {e: 7}, 7 {f: 5}, 8 {c: 2, g: 2, h: 2}, 9 {f: 1, h: 6}, 10 {f: 9, g: 8} 11 ] 12 13 14 print b in Adj_dict_weight[a] #结点b是否是结点a的邻居结点 15 print len(Adj_dict_weight[a]) #结点a的出度 16 print Adj_dict_weight[a][b] #边(a,b)的权重
运行结果如下:
True
5
2
(4)邻接集字典
以上图的表示方法都使用了list类型,其实,也可以使用字典结构dict和集合结构set的嵌套来实现。
1 Adj_set_dict = {'a':set('bcdef'), 2 'b':set('ce'), 3 'c':set('d'), 4 'd':set('e'), 5 'e':set('f'), 6 'f':set('cgh'), 7 'g':set('fh'), 8 'h':set('fg') 9 } 10 11 print Adj_set_dict["a"] #节点a的邻居节点 12 print "b" in Adj_set_dict["a"] #节点b是否是节点a的邻居节点
运行结果如下:
set(['c', 'b', 'e', 'd', 'f'])
True
(5)嵌套字典(最重要*****)
也可以使用嵌套字典的方式来实现加权图。
1 Nest_dict = {'a':{'b':2, 'c':1, 'd':3, 'e':9, 'f':4}, 2 'b':{'c':4, 'e':3}, 3 'c':{'d':8}, 4 'd':{'e':7}, 5 'e':{'f':5}, 6 'f':{'c':2, 'g':2, 'h':2}, 7 'g':{'f':1, 'h':6}, 8 'h':{'f':9, 'g':8} 9 }
3、图的遍历
图遍历又称图的遍历,属于数据结构中的重要内容。它指的是从图中的任一顶点出发,对图中的所有顶点访问一次且只访问一次。图的遍历操作和树的遍历操作功能相似。图的遍历是图的一种基本操作,图的许多其它操作都是建立在遍历操作的基础之上。
由于图结构本身的复杂性,所以图的遍历操作也较复杂,主要表现在以下四个方面:
(a)在图结构中,没有一个“自然”的首结点,图中任意一个顶点都可作为第一个被访问的结点。
(b)在非连通图中,从一个顶点出发,只能够访问它所在的连通分量上的所有顶点,因此,还需考虑如何选取下一个出发点以访问图中其余的连通分量。
(c)在图结构中,如果有回路存在,那么一个顶点被访问之后,有可能沿回路又回到该顶点。
(d)在图结构中,一个顶点可以和其它多个顶点相连,当这样的顶点访问过后,存在如何选取下一个要访问的顶点的问题。
(1)深度优先遍历(DFS)
深度优先遍历也称为深度优先搜索(Depth First Search),它类似于树的先序遍历,具体定义如下:假设初始状态是图中所有顶点均未被访问,则从某个顶点v出发,首先访问该顶点,然后依次从它的各个未被访问的邻接点出发深度优先搜索遍历图,直至图中所有和v有路径相通的顶点都被访问到。 若此时尚有其他顶点未被访问到,则另选一个未被访问的顶点作起始点,重复上述过程,直至图中所有顶点都被访问到为止。
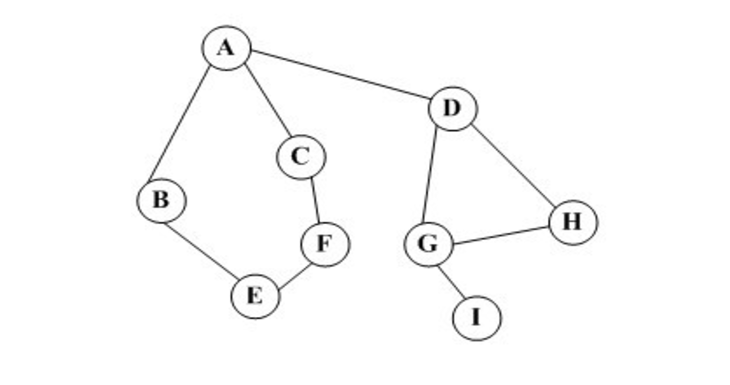
1 #创建一个图 2 Graph = {} 3 Graph['A'] = ['B', 'C', 'D'] 4 Graph['B'] = ['A', 'E'] 5 Graph['C'] = ['A', 'F'] 6 Graph['D'] = ['A', 'G', 'H'] 7 Graph['E'] = ['B', 'F'] 8 Graph['F'] = ['E', 'C'] 9 Graph['G'] = ['D', 'H', 'I'] 10 Graph['H'] = ['G', 'D'] 11 Graph['I'] = ['G'] 12 13 14 #使用堆栈来实现深度优先遍历 15 def DFSTraverse(G, start): 16 stack = [] #初始化一个堆栈 17 visited = set() #初始化一个访问过的节点集合 18 stack.append(start) #将起始结点入栈 19 while stack: #如果栈不为空,进入循环 20 node = stack.pop() #栈顶元素出栈 21 if node in visited: #判断栈顶元素是否被访问过 22 continue #元素被访问过,跳出循环,查看栈内的其他元素 23 else: #栈顶元素未被访问 24 print node, #访问栈顶元素 25 visited.add(node) #将其加入访问过的集合 26 for adj in G[node]: #将该元素的邻居节点加入到栈中去 27 if adj not in visited: 28 stack.append(adj) 29 print "\n" 30 31 32 if __name__ == '__main__': 33 34 print "深度优先搜索结果:" 35 DFSTraverse(Graph, 'A')
运行结果如下:
深度优先搜索结果:
A D H G I C F E B
(2)广度优先遍历(BFS)

因此,使用一个队列(Queue)辅助实现广度优先遍历(BFS)代码如下(python 2.7):
1 #创建一个图 2 Graph = {} 3 Graph['A'] = ['B', 'C', 'D'] 4 Graph['B'] = ['A', 'E'] 5 Graph['C'] = ['A', 'F'] 6 Graph['D'] = ['A', 'G', 'H'] 7 Graph['E'] = ['B', 'F'] 8 Graph['F'] = ['E', 'C'] 9 Graph['G'] = ['D', 'H', 'I'] 10 Graph['H'] = ['G', 'D'] 11 Graph['I'] = ['G'] 12 13 14 #使用队列来实现广度优先遍历 15 def BFSTraverse(G, start): 16 from collections import deque 17 queue = deque() #初始化一个队列 18 visited = set() #初始化一个存储访问过元素的集合 19 queue.append(start) #将起始结点加入队列 20 while queue: #当队列不为空时,进入循环 21 node = queue.popleft() #将队列的队首元素出队 22 if node in visited: #判断该元素是否被访问过,如果访问过,跳出本次循环 23 continue 24 else: 25 print node, 26 visited.add(node) 27 for adj in G[node]: 28 if adj not in visited: 29 queue.append(adj) 30 print "\n" 31 32 33 34 35 if __name__ == '__main__': 36 37 print "广度优先搜索结果:" 38 BFSTraverse(Graph, 'A')
运行结果如下:
广度优先搜索结果:
A B C D E F G H I
(3)DFS和BFS算法效率比较
空间复杂度:两者的空间复杂度都是O(n),分别借用了堆栈和队列。
时间复杂度:对于两者而言,时间复杂度只与图的存储结构(邻接矩阵或邻接表)有关,而与搜索路径无关。邻接矩阵:O(n^2),邻接表:O(n + e)。
4、最小生成树
4.1 什么是生成树
在图论的数学领域中,如果连通图 G的一个子图是一棵包含G 的所有顶点的树,则该子图称为G的生成树(SpanningTree)。生成树是连通图的包含图中的所有顶点的极小连通子图。图的生成树不惟一。从不同的顶点出发进行遍历,可以得到不同的生成树。


对于连通的带权图(连通网)G,其生成树也是带权的。生成树T各边的权值总和称为该树的权,记作:

其中,TE表示T的边集,w(u,v)表示边(u,v)的权。权最小的生成树称为G的最小生成树(Minimum SpannirngTree)。最小生成树可简记为MST。
求一个连通图的最小生成树的方法包括:Kruskal算法和Prim 算法。
4.3 最小生成树算法
接下来我们将以一个无向图来展示Kruskal算法和Prim 算法,无向图如下所示:
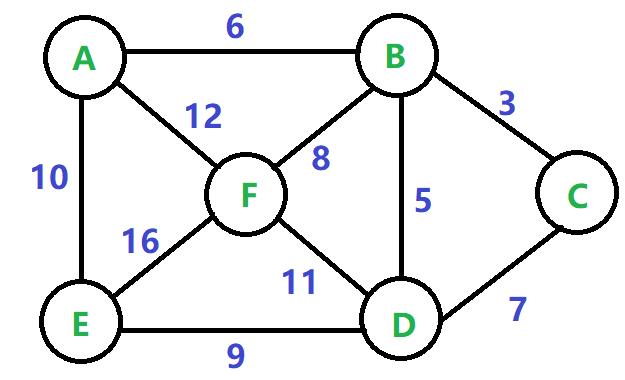
(1)Kruskal算法
Kruskal算法是一种用来查找最小生成树的算法,它是基于贪心的思想得到的。首先我们把所有的边按照权值先从小到大排列,接着按照顺序选取每条边,如果这条边的两个端点不属于同一集合,那么就将它们合并,直到所有的点都属于同一个集合为止。至于怎么合并到一个集合,那么这里我们就可以用到一个工具——-并查集。换而言之,Kruskal算法就是基于并查集的贪心算法。
Kruskal算法每次要从都要从剩余的边中选取一个最小的边。通常我们要先对边按权值从小到大排序,这一步的时间复杂度为为O(|Elog|E|)。Kruskal算法的实现通常使用并查集,来快速判断两个顶点是否属于同一个集合。最坏的情况可能要枚举完所有的边,此时要循环|E|次,所以这一步的时间复杂度为O(|E|α(V)),其中α为Ackermann函数,其增长非常慢,我们可以视为常数。所以Kruskal算法的时间复杂度为O(|Elog|E|),其中E和V分别是图的边集和点集。
因此,使用Kruskal算法查找最小生成树的代码如下(python 2.7):
1 Graph = {'A': {'B': 6, 'E': 10, 'F': 12}, 2 'B': {'A': 6, 'C': 3, 'D': 5, 'F': 8}, 3 'C': {'B': 3, 'D': 7}, 4 'D': {'B': 5, 'C': 7, 'E': 9, 'F': 11}, 5 'E': {'A': 10, 'D': 9, 'F': 16}, 6 'F': {'A': 12, 'B': 8, 'D': 11, 'E': 16}, 7 } 8 9 def Kruskal(G): 10 def f1(x): 11 return x[2] 12 record_node = set() #记录添加的边节点 13 mintree = [] #最小生成树的所有的边 14 cost = [] 15 edges = [] #获得图的所有的边,并对它排序 16 for key1 in G.keys(): 17 for key2 in G[key1].keys(): 18 edges.append([key1, key2, G[key1][key2]]) 19 edges.sort(key=f1, reverse=True) #对所有的边的成本进行从大到小排序 20 21 while edges: 22 edge = edges.pop() #选取最短的边 23 if (edge[0] in record_node) and (edge[1] in record_node): #如果这两个顶点同时在集合中,表示会形成环路,不能加入这条边 24 continue 25 else: 26 record_node.add(edge[0]) 27 record_node.add(edge[1]) 28 cost.append(edge.pop()) 29 mintree.append(edge) 30 print "克鲁斯卡尔Kruskal算法最小生成树:" 31 print "各个边的权值: ", cost 32 print "最小生成树的成本: ", sum(cost) 33 print "最小生成树的边: ", mintree 34 return cost, mintree 35 36 if __name__ == '__main__': 37 cost,mintree = Kruskal(Graph) 38 print "\n"
运行结果如下:
克鲁斯卡尔Kruskal算法最小生成树:
各个边的权值: [3, 5, 6, 8, 9]
最小生成树的成本: 31
最小生成树的边: [['B', 'C'], ['D', 'B'], ['B', 'A'], ['F', 'B'], ['D', 'E']]
(2)Prim算法
普里姆算法(Prim算法)是图论中的一种算法,可在加权连通图里搜索最小生成树。意即由此算法搜索到的边子集所构成的树中,不但包括了连通图里的所有顶点,且其所有边的权值之和亦为最小。

对于任意图,假设包含n个顶点,m条边。Prim算法是从顶点出发的,其算法时间复杂度与顶点数目有关系。(注意:prim算法适合稠密图,其时间复杂度为O(n^2),其时间复杂度与边得数目无关,而Kruskal算法的时间复杂度为O(ElogE)跟边的数目有关,适合稀疏图。)
Prim算法是一种构造性算法。假设G=(V,E)是一个具有n个顶点的带权连通无向图,T=(U,TE)是G的最小生成树,其中U是T的顶点集,TE是T的边集,则由G构造从起始顶点v出发的最小生成树T的步骤如下:
(a)初始化U={v},以v到其他顶点的所有边为候选边;
(b)重复以下步骤(n-1)次,使得其他(n-1)个顶点被加入到U中:
(1)从侯选边中挑选权值最小的边加入TE,设该边在V-U中的顶点是k,将k加入U中;(加入后不能形成环)
(2)考察当前V-U中所有顶点j,修改侯选边,若边(k,j)的权值小于原来和顶点j关联的侯选边,则用边(k,j)取代后者作为侯选边。(加入后不能形成环)
因此,使用Prim算法查找最小生成树的代码如下(python 2.7):
1 Graph = {'A': {'B': 6, 'E': 10, 'F': 12}, 2 'B': {'A': 6, 'C': 3, 'D': 5, 'F': 8}, 3 'C': {'B': 3, 'D': 7}, 4 'D': {'B': 5, 'C': 7, 'E': 9, 'F': 11}, 5 'E': {'A': 10, 'D': 9, 'F': 16}, 6 'F': {'A': 12, 'B': 8, 'D': 11, 'E': 16}, 7 } 8 9 def Prim(G): 10 U = set(G.keys()) #图G的顶点集合U,它包含了该图的所有顶点 11 V = set(G.keys()[0]) #将起始顶点加入集合V 12 min_tree = [] #存储要返回的最小生成树的所有的边 13 cost = [] #记录最小生成树各边的权重的值 14 while U.difference(V): #当集合U和V不想等时,进入循环 15 min_value = float("inf") #初始化一个最小值 16 node1 = None #用于记录加入边的第一个节点 17 node2 = None #用于记录加入边的第二个节点 18 for v in V: #遍历访问过的节点 19 for u in U.difference(V): #遍历未访问过的节点 20 if u in G[v]: #如果两个节点之间存在相连的边 21 if G[v][u] < min_value: #判断该值是否是所有访问过节点存在的相邻边中的最小值 22 min_value = G[v][u] #更新边权重的最小值 23 node1 = v #记录边权重最小值的第一个节点 24 node2 = u #记录边权重最小值的第二个节点 25 V.add(node2) #将第二个节点加入到访问过的节点集合V,因为第二个节点来自于未访问过的节点集合 26 min_tree.append([node1, node2]) #将包括两个节点的边加入到最小生成树边列表 27 cost.append(min_value) #将边的权重加入到成本列表中 28 print "普利姆Prim算法最小生成树:" 29 print "各个边的权值: ", cost 30 print "最小生成树的成本: ", sum(cost) 31 print "最小生成树的边: ", min_tree 32 return cost, min_tree 33 34 if __name__ == '__main__': 35 36 Prim(Graph)
运行结果如下:
普利姆Prim算法最小生成树:
各个边的权值: [6, 3, 5, 8, 9]
最小生成树的成本: 31
最小生成树的边: [['A', 'B'], ['B', 'C'], ['B', 'D'], ['B', 'F'], ['D', 'E']]
(3)两种算法比较

5、最短路径问题




 浙公网安备 33010602011771号
浙公网安备 33010602011771号