2022.10.14练习

T1传送锚点     T2传送锚点

题目描述

在企鹅国，企鹅们是通过滑冰出行的。每次滑冰需要选择一个营地作为起点，一个营地作为终点，然后从营地 A(a_x​,a_y​) 滑到营地 B(b_x​,b_y​) 需要的时间是 min{∣a_x​−b_x​∣,∣a_y−b_y​∣}。

现在企鹅豆豆在 1 号营地，他需要赶到 N 号营地参加活动，他想知道他最少需要花费多少时间？

可能存在营地重合的情况。

输入格式

第一行一个整数 n ，代表营地个数。

接下来 n 行，每行 2 个数字 x_i​，y_i​ ，表示一个营地的坐标。

输出格式

输出一个整数表示需要的最少时间。

样例

输入数据 1

5
2 2
1 1
4 5
7 1
6 7

输出数据 1

2

样例1说明

从营地 1 先到达营地 4 ，花费 1 单位时间。

再从营地 4 到达营地 5，花费 1 单位时间。

数据规模与约定

对于 5% 的数据，x_i=y_i​。

对于 30%的数据，n≤1000。

对于另外 35% 的数据，x_i​,y_i 均单调不减。

对于 100% 的数据，1≤n≤2×10⁵,0≤x_i,y_i​≤10⁹。

 

【算法分析】

考虑对于三个点 i，j，k，i，j，k，若 x_i<x_j<x_k​， 则 i→k=x_k​−x_i​=(x_k​−x_j)+(x_j−x_i)=i→j→k，边 i→k是根本不用连的。

所以将所有点的 x 坐标排序，然后从小到大连边即可。

对于 y 坐标同理。

然后对于限制条件 min(∣a_x​−b_x​∣,∣a_y​−b_y​∣)， 只需要跑最短路即可，因为最短路不可能把你导向一条长的路径。

Code:

#include<bits/stdc++.h>
using namespace std;
const int N=2e5+5;
int n,tot;
bool vis[N];
long long ans,d[N];
int fi[N],ne[N<<2],to[N<<2],w[N<<2];
priority_queue<pair<int,int> > q;
struct xiao 
{
    int x,y,id;
}a[N];

inline void add(int x,int y,int z) 
{
    ne[++tot]=fi[x],fi[x]=tot,to[tot]=y,w[tot]=z;
    ne[++tot]=fi[y],fi[y]=tot,to[tot]=x,w[tot]=z;
}

inline bool node1(const xiao &a,const xiao &b) 
{
    return a.x<b.x;
}

inline bool node2(const xiao &a,const xiao &b) 
{
    return a.y<b.y;
}

inline void dijkstra() 
{
    memset(d,0x3f,sizeof(d));
    d[1]=0;
    q.push(make_pair(0,1));
    while(!q.empty()) 
    {
        int x=q.top().second;
        q.pop();
        if(vis[x]) continue;
        vis[x]=1;
        for(int i=fi[x];i;i=ne[i]) {
            int v=to[i];
            if(d[v]>d[x]+w[i]) 
            {
                d[v]=d[x]+w[i];
                q.push(make_pair(-d[v],v));
            }
        }
    }
}
int main() 
{
    cin>>n;
    for(int i=1;i<=n;i++) 
    {
        cin>>a[i].x>>a[i].y;
        a[i].id=i;
    }
    sort(a+1,a+n+1,node1);
    for(int i=1;i<n;i++) 
        add(a[i].id,a[i+1].id,a[i+1].x-a[i].x);
    sort(a+1,a+n+1,node2);
    for(int i=1;i<n;i++) 
        add(a[i].id,a[i+1].id,a[i+1].y-a[i].y);
    dijkstra();
    cout<<d[n]<<'\n';
    return 0;
}

题目描述

给定一张 n 个点 m 条边的连通图，每条边有权值 w ，定义从 u₁ 到 u_x​ 经过边 e₁，e₂​，…，e_k 的路径长度为：

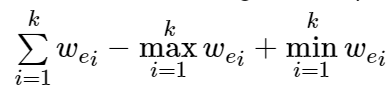
请分别对于每个点 i∈[2,n] 求出点 1 到 i 的长度最小的路径。

输入格式

第一行两个数，代表 n，m。

接下来 mm 行每行三个数 u，v，w，代表一条连接 u，v 长度为 w 的边。

输出格式

对于每个 i 输出点 1 到 i 长度最小的路径的长度，用空格分隔。

样例

输入：

5 4
5 3 4
2 1 1
3 2 2
2 4 2

输出：

1 2 2 4

样例1说明

• 当 i=2 时经过路径 1→2
• 当 i=3 时经过路径 1→2→3
• 当 i=4 时经过路径 1→2→4
• 当 i=5 时经过路径 1→3→5

数据规模与约定

对于 30% 的数据，1≤n≤1000

对于另 30%的数据，m=n−1

对于 100% 的数据，1≤n,m≤1×10⁵；0≤wi​≤10⁹

【算法分析】

当 m=n−1 时，1 到 i 的路径唯一，直接 dfs 即可。

考虑图的情况，我们可以转化一下题意，转化为 1 到 i 的路径中将某一条边权值变为 0 并将某一条边权值变为 2w 的最小值。

操作只能进行一次，所以考虑分层图解法，做一次操作就向上走一层，因为高层不能回到低层，所以可以保证每种操作只做一次，而做一次操作才能上一层，所以顶层的点可以保证两次操作都被进行。

然后考虑如何找到最大和最小权值的边，答案很简单，直接跑最短路即可，因为程序一定会在最大权值的边上一层，在最小权值的边再上一层，否则总会有一条更短路存在。

然后分先走 max 上第二层和先走 min 上第二层建两个分层图讨论一下即可。

最后特判掉走一条边即可从 1 到 i 的情况即可，因为此时 min，max 走的是同一条边，在分层图上无法实现。

Code：

 

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=1e6+10;
int n,m,tot;
int fi[N],to[N*2],ne[N*2],w[N*2],d[N];
bool vis[N];

void add(int x,int y,int z) 
{
    ne[++tot]=fi[x];
    fi[x]=tot;
    to[tot]=y;
    w[tot]=z;
}

void spfa() 
{
    memset(d,0x3f,sizeof(d));
    queue<int> q;
    d[1]=0;
    q.push(1);
    vis[1]=1;
    while (!q.empty())
    {
        int x=q.front();
        q.pop();
        vis[x]=0;
        for(int i=fi[x];i;i=ne[i])
        {
            int v=to[i];
            if (d[v]>d[x]+w[i])
            {
                d[v]=d[x]+w[i];
                if(!vis[v])
                {
                    vis[v]=1;
                    q.push(v);
                }
            }
        }
    }
}

signed main() 
{
    cin>>n>>m;
    for(int i=1;i<=m;i++)
    {
        int x,y,z;
        cin>>x>>y>>z;
        for(int i=0;i<=3;i++)
        {
            add(x+i*n,y+i*n,z);
            add(y+i*n,x+i*n,z);
        }
        add(x,y+n,0),add(y,x+n,0);
        add(x,y+2*n,2*z),add(y,x+2*n,2*z);
        add(x+n,y+3*n,2*z),add(y+n,x+3*n,2*z);
        add(x+2*n,y+3*n,0),add(y+2*n,x+3*n,0);
    }
    spfa();
    for(int i=2;i<=n;i++)
    {
        int ans=min(d[i],d[i+3*n]);
        printf("%lld ",ans); 
    }
    return 0;
}