AC自动机

参考自：OI Wiki

概述

AC 自动机是 以 Trie 的结构为基础，结合 KMP 的思想 建立的。

解释

简单来说，建立一个 AC 自动机有两个步骤：

基础的 Trie 结构：将所有的模式串构成一棵 Trie。
KMP 的思想：对 Trie 树上所有的结点构造失配指针。

然后就可以利用它进行多模式匹配了。

字典树构建

AC 自动机在初始时会将若干个模式串丢到一个 Trie 里，然后在 Trie 上建立 AC 自动机。这个 Trie 就是普通的 Trie，该怎么建怎么建。

这里需要仔细解释一下 Trie 的结点的含义，尽管这很小儿科，但在之后的理解中极其重要。Trie 中的结点表示的是某个模式串的前缀。我们在后文也将其称作状态。一个结点表示一个状态，Trie 的边就是状态的转移。

形式化地说，对于若干个模式串s₁,s₂…s_n ，将它们构建一棵字典树后的所有状态的集合记作Q。

失配指针

AC 自动机利用一个 fail 指针来辅助多模式串的匹配。

状态 u 的 fail 指针指向另一个状态v ，其中v∈Q，且 v 是 u 的最长后缀（即在若干个后缀状态中取最长的一个作为 fail 指针）。

AC 自动机在做匹配时，同一位上可匹配多个模式串。

构建指针

构建 fail 指针，可以参考 KMP 中构造 Next 指针的思想。

考虑字典树中当前的结点x ，x 的父结点是 y，y 通过字符 c 的边指向x ，即tr[y][c]==x 。假设深度小于 x 的所有结点的 fail 指针都已求得。

如果 tr[fail[y]][c] 存在：则让 u 的 fail 指针指向tr[fail[y]][c] 。相当于在 y 和 fail[y]后面加一个字符 c，分别对应 x 和 fail[x]。
如果 tr[fail[y]][c] 不存在：那么我们继续找到tr[fail[fail[y]]][c] 。重复 1 的判断过程，一直跳 fail 指针直到根结点。
如果真的没有，就让 fail 指针指向根结点。

如此即完成了 fail[x] 的构建

例子

对字符串 i , he , his , she , hers 组成的字典树构建 fail 指针：

黄色结点：当前的结点。
绿色结点：表示已经 BFS 遍历完毕的结点，
橙色的边：fail 指针。
红色的边：当前求出的 fail 指针。

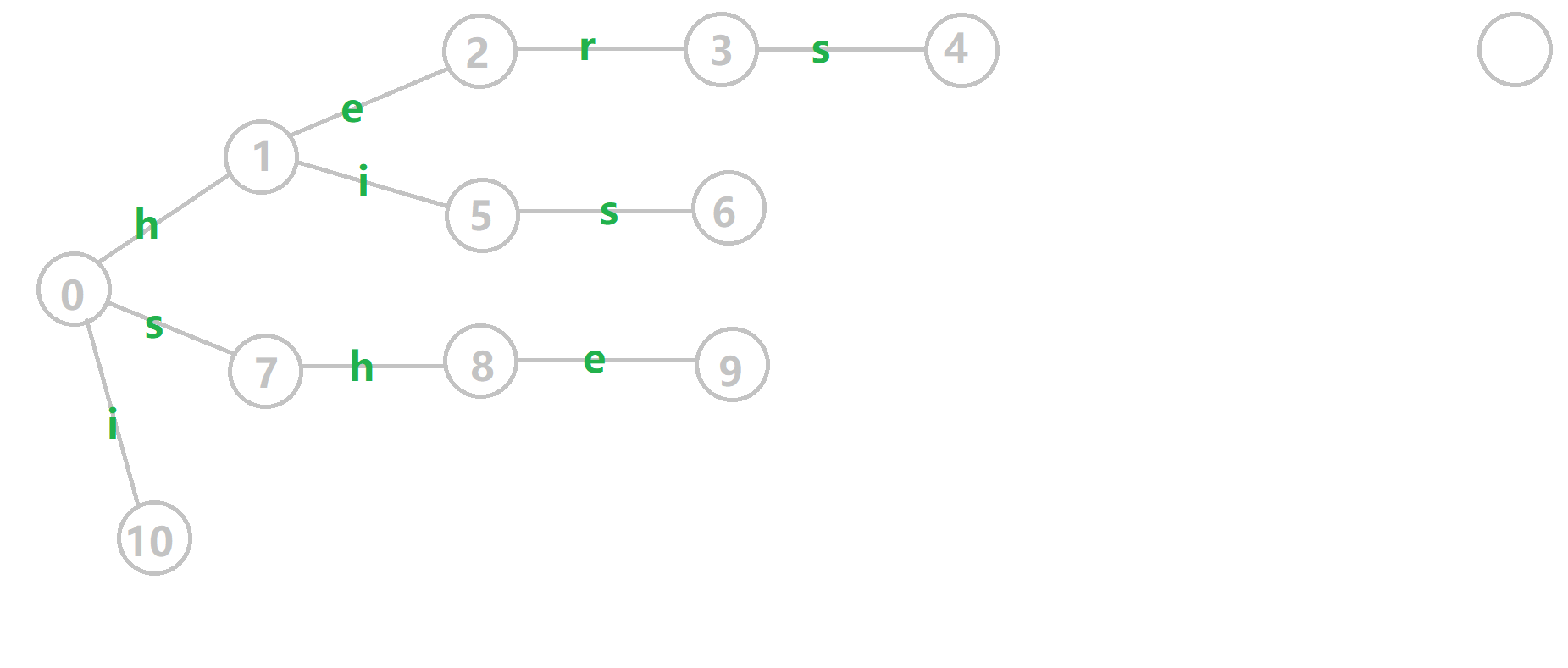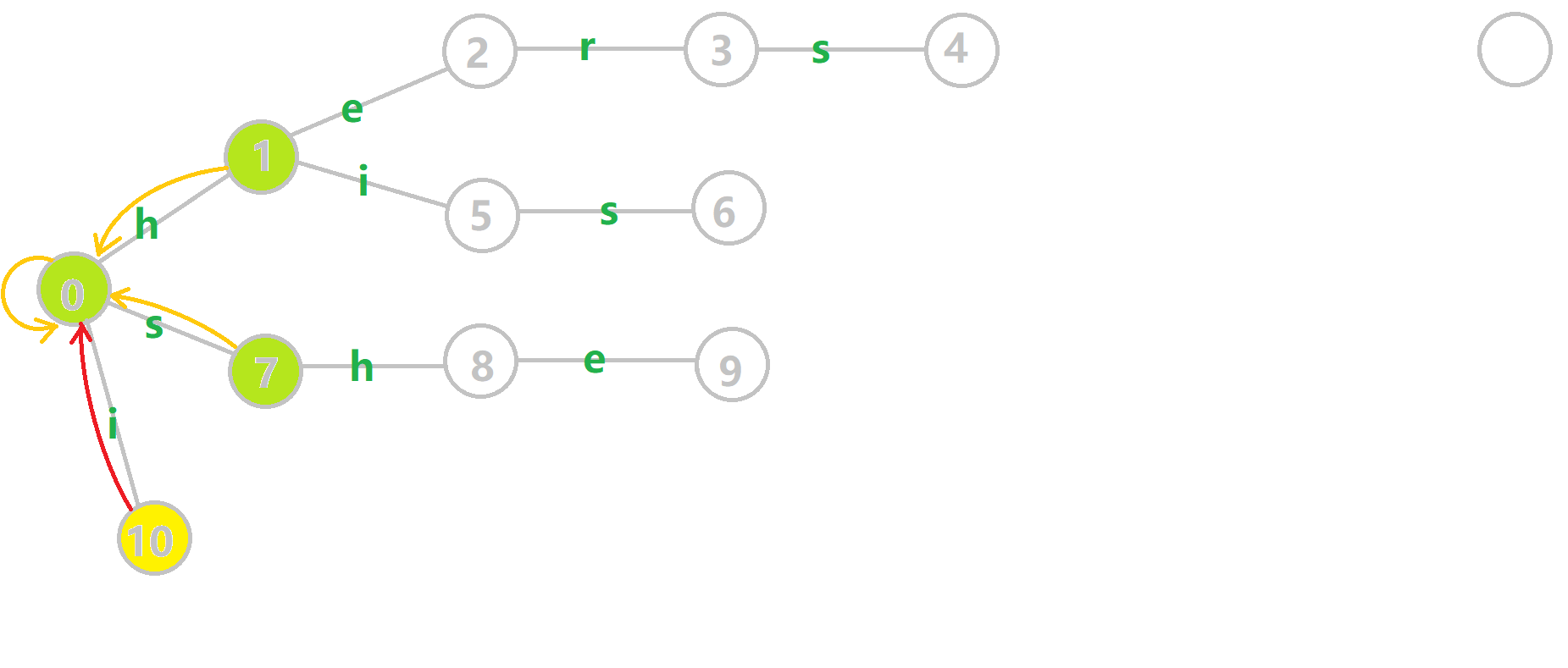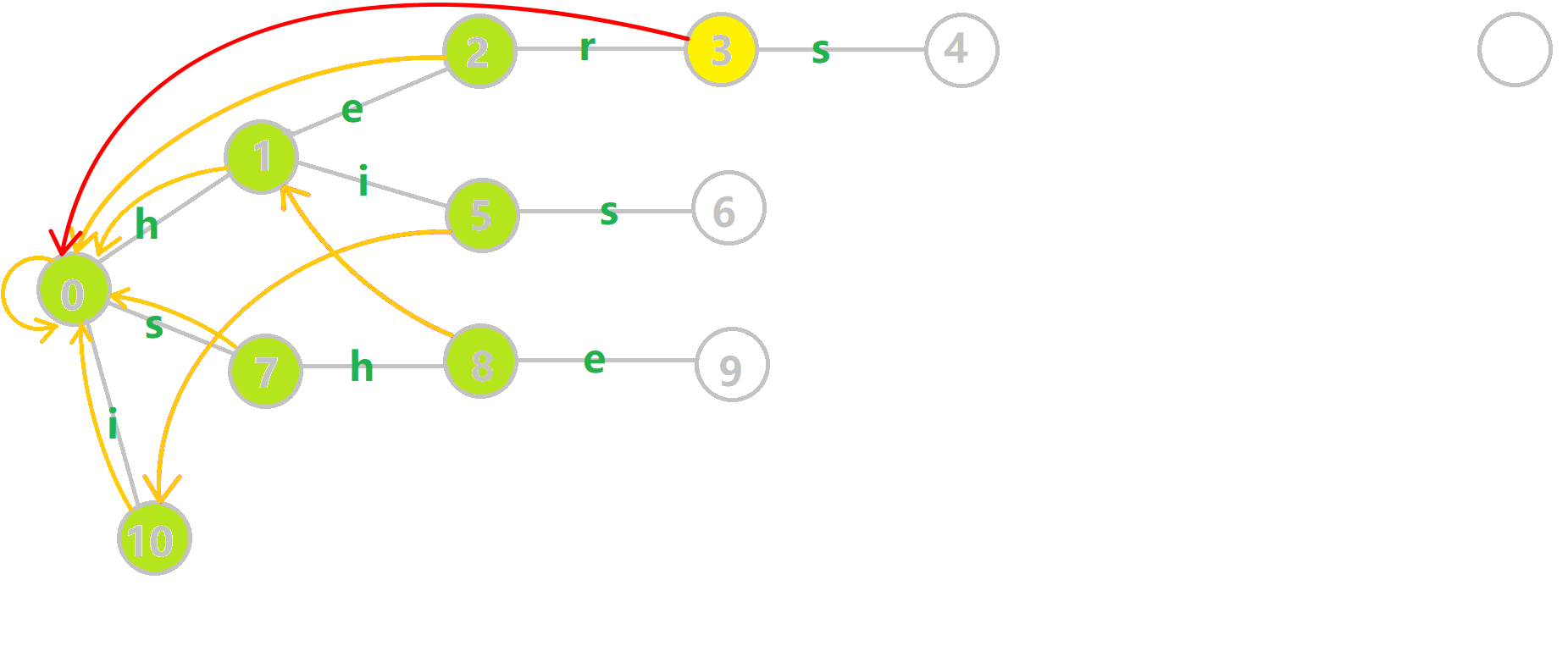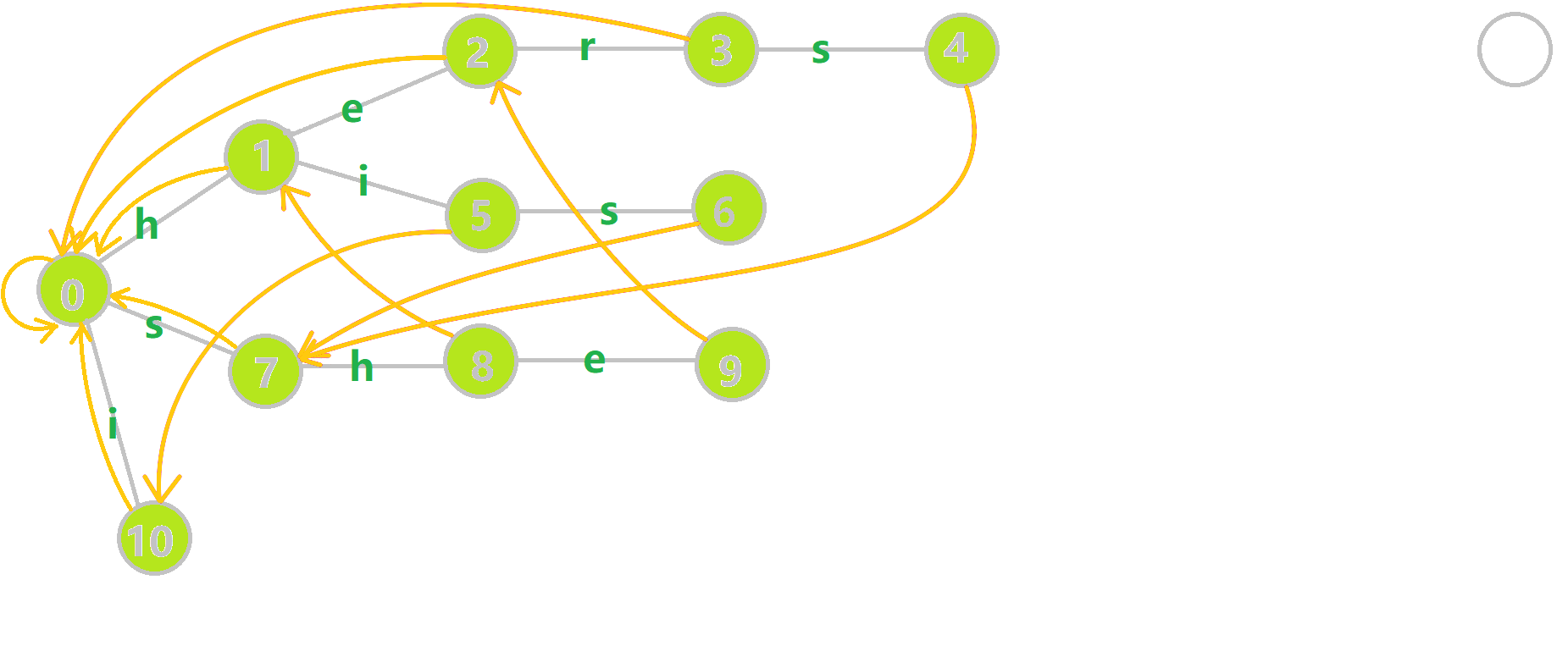
我们重点分析结点 6 的 fail 指针构建：

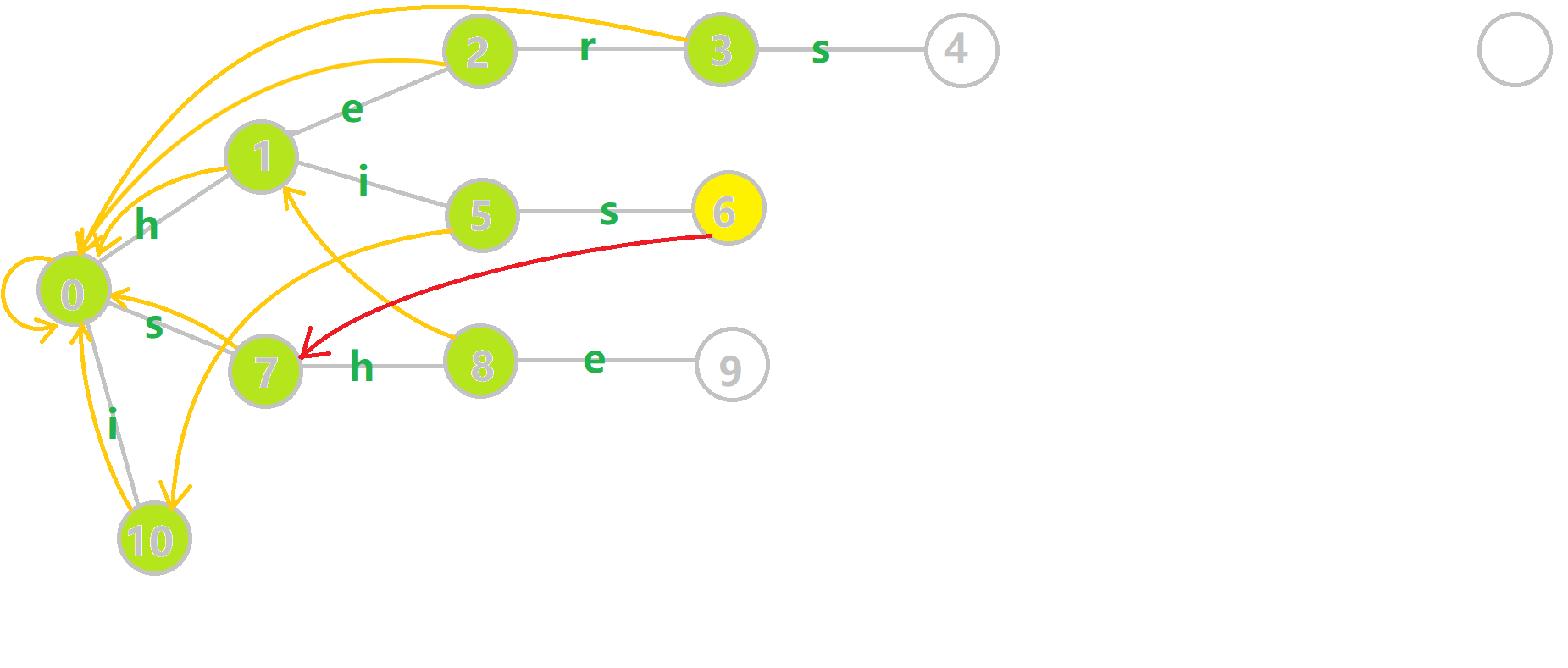
找到 6 的父结点 5，fail[5]=10。然而 10 结点没有字母 s 连出的边；继续跳到 10 的 fail 指针，fail[10]=0。发现 0 结点有字母 s 连出的边，指向 7 结点；所以 fail[6]=7。最后放一张建出来的图

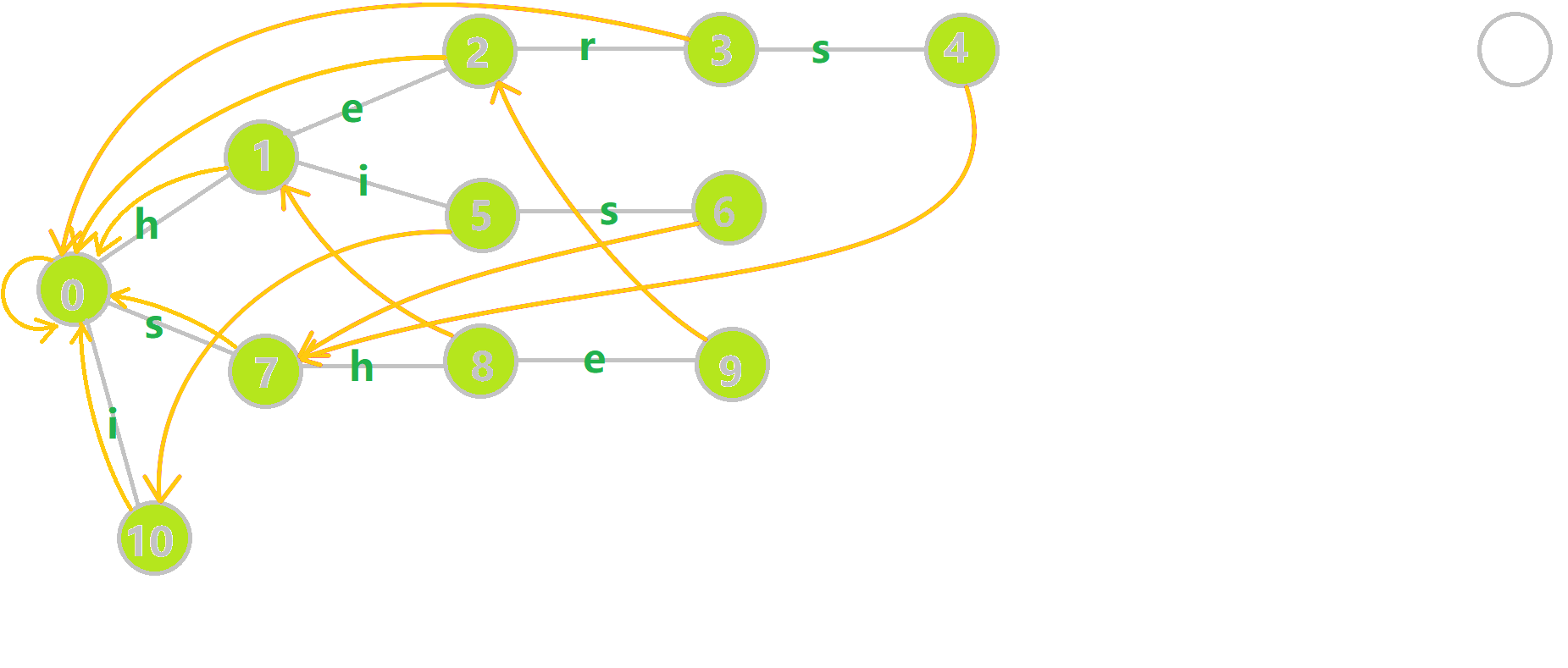
finish

于是乎，重点差不多了。

下面看看：

AC自动机- Keywords Search

背景

题目来源：HDU2222

题目描述

有一个由

输入格式

输入有多组数据，第

对于每组数据：第

输出格式

对于每组输入数据，输出一行答案，该答案为一个整数，该整数表示单词库中有几个单词在文章中出现过。

样例

输入数据 1

1
5
she
he
say
shr
her
yasherhs

输出数据 1

数据规模与约定

对于 100% 的数据：

Code:

#include<bits/stdc++.h>
using namespace std;

const int maxn=1000010;
const int maxm=50*10010;
char t[60],s[maxn];
int n;
int ch[maxm][26];         //Trie树节点 
int val[maxm];            //每个字符串的结尾节点都有一个非0的val 
int fail[maxm];           //前缀指针，fail[i]表示i的前缀指针
int last[maxm];           //lase[i]=j，j节点表示的单词是i节点单词的后缀，且j节点是单词节点 
int sz;                   //节点编号

void insert(char *s)      //构建Trie树 
{
    int u=0;
    int n=strlen(s);
    for(int i=0;i<n;i++)
    {
        int c=s[i]-'a';   //把a..z转为0..25
        if(!ch[u][c])
        {
            memset(ch[sz],0,sizeof(ch[sz]));
            val[sz]=0;
            ch[u][c]=sz++;
        }
        u=ch[u][c];
    }
    val[u]++;               //val[u]表示节点0～节点u构成的单词数量
}

                            //当节点u匹配失败时，我们需要找到另一个串v，使得它有尽量长的前缀与u所代表的串的后缀相等
void getfail()              //计算前缀指针指向v 
{
    queue<int> q;           //普通队列
    fail[0]=0;              //根
    int u=0;
    for(int i=0;i<26;i++)   //根的26个节点的前缀指针都指向根，并入队
    {
        u=ch[0][i];
        if(u)
        {
            q.push(u);      //入队
            fail[u]=0;
            last[u]=0;
        }
}
    while(!q.empty())                                   //广搜计算fail 
    {
        int r=q.front();q.pop();                        //队首r出队
        for(int i=0;i<26;i++)                           //枚举r的26个子节点u，求fail[u]
        {
            u=ch[r][i];
            if(!u)                                       //如果u不存在，则跳向其父节点r前缀指针指向的第i个子节点
            {
                ch[r][i]=ch[fail[r]][i];
                continue;                                //继续枚举r的下一个子节点
            }
            q.push(u);                                   //如果u存在，则入队
            int v=fail[r];
            while(v&&!ch[v][i]) v=fail[v];               //v存在并且v没有第i个子节点，则跳到v的前缀指针指向的节点
            fail[u]=ch[v][i];                            //v存在并且v的第i个子节点也存在，就可以确定前缀指针
            last[u]=val[fail[u]]?fail[u]:last[fail[u]];  //如果fail[u]是一个完整单词且是u的后缀     否则
        } 
    }
}

int find(char *s)             //在s中查找出现了哪几个模板的单词 
{
    int u=0,cnt=0;            //从根开始，cnt为答案
    int n=strlen(s);
    for(int i=0;i<n;i++)      //扫描文章中的每个字符，
    {
        int c=s[i]-'a';       //把a..z转为0..25
        u=ch[u][c];
        int temp=0;              //必须赋初值为0，否则如果下面两个判断都不成立，while也可正常执行
        if(val[u])            //如果u是一个完整单词
            temp=u;
        else if(last[u])      //如果u的后缀last[u]存在 
                temp=last[u];
        while(temp)
        {
            cnt+=val[temp];   //累加单词数量
            val[temp]=0;      //标记，加过了不能再加
            temp=last[temp];  //跳到当前temp的后缀（比temp段），更新temp
        }
    }
    return cnt;
}

int main()
{    
    int T;
    scanf("%d",&T);
    
    while(T--)
    {       
        memset(ch[0],0,sizeof(ch[0])); //初始化0号节点的相关信息（多组数据，每次需要初始化） 
        memset(last,0,sizeof(last));
        sz=1;
             
        scanf("%d",&n);                //读入n个单词
        for(int i=1;i<=n;i++)          //构建Trie树 
        {
            scanf("%s",t);
            insert(t);    
        }
        getfail();                     //计算前缀指针
        scanf("%s",s);                 //读入文章
        int ans=find(s);               //查找 
        printf("%d\n",ans);
    }
    return 0;
}

posted @ 2022-10-13 08:21 光暗之影x 阅读(13) 评论(0) 收藏举报

刷新页面返回顶部

光暗之影