DP引入

选自题单：传送锚点

P1164 小A点菜

题目背景

uim 神犇拿到了 uoi 的 ra（镭牌）后，立刻拉着基友小 A 到了一家……餐馆，很低端的那种。

uim 指着墙上的价目表（太低级了没有菜单），说：“随便点”。

题目描述

不过 uim 由于买了一些书，口袋里只剩 M 元(M≤10000)。

餐馆虽低端，但是菜品种类不少，有 N 种(N≤100)，第 i 种卖a_i元(a_i≤1000)。由于是很低端的餐馆，所以每种菜只有一份。

小 A 奉行“不把钱吃光不罢休”，所以他点单一定刚好把 uim 身上所有钱花完。他想知道有多少种点菜方法。

由于小 A 肚子太饿，所以最多只能等待 1 秒。

输入格式

第一行是两个数字，表示 N 和 M。

第二行起 N 个正数 a_i​（可以有相同的数字，每个数字均在 10001000 以内）。

输出格式

一个正整数，表示点菜方案数，保证答案的范围在 int 之内。

输入输出样例

输入 #1复制

4 4
1 1 2 2

输出 #1复制

3

说明/提示

2020.8.29，增添一组 hack 数据 by @yummy

表废话，接下来解题：

这是一道简单的动规题，定义f[i][j]为用前i道菜用光j元钱的办法总数，其状态转移方程如下：

（1）if(j==第i道菜的价格)f[i][j]=f[i-1][j]+1;

（2）if(j>第i道菜的价格) f[i][j]=f[i-1][j]+f[i-1][j-第i道菜的价格];

（3）if(j<第i道菜的价格) f[i][j]=f[i-1][j];

说的简单一些，这三个方程，每一个都是在吃与不吃之间抉择。若钱充足，办法总数就等于吃这道菜的办法数与不吃这道菜的办法数之和；若不充足，办法总数就只能承袭吃前i-1道菜的办法总数。依次递推，在最后，我们只要输出f[n][m]的值即可。

这不就是0/1背包吗？！？！？！

Code：

#include<bits/stdc++.h>
using namespace std;
int n,m;
int a[105];
int f[105][10005];

int main()
{
    cin>>n>>m;
    for(int i=1;i<=n;i++)
        cin>>a[i];
    for(int i=1;i<=n;i++)
        for(int j=1;j<=m;j++)
            if(j>a[i]) f[i][j]=f[i-1][j]+f[i-1][j-a[i]];
            else if(j==a[i]) f[i][j]=f[i-1][j]+1;
            else f[i][j]=f[i-1][j];
    cout<<f[n][m]<<'\n';
}

P1077 [NOIP2012 普及组] 摆花

题目描述

小明的花店新开张，为了吸引顾客，他想在花店的门口摆上一排花，共 m 盆。通过调查顾客的喜好，小明列出了顾客最喜欢的 n 种花，从 1 到 n 标号。为了在门口展出更多种花，规定第 i 种花不能超过a_i​ 盆，摆花时同一种花放在一起，且不同种类的花需按标号的从小到大的顺序依次摆列。

试编程计算，一共有多少种不同的摆花方案。

输入格式

第一行包含两个正整数 n 和 m，中间用一个空格隔开。

第二行有 n 个整数，每两个整数之间用一个空格隔开，依次表示 a₁​,a₂​,⋯,a_n​。

输出格式

一个整数，表示有多少种方案。注意：因为方案数可能很多，请输出方案数对 10⁶+7 取模的结果。

输入输出样例

输入 #1复制

2 4
3 2

输出 #1复制

2

说明/提示

【数据范围】

对于 20% 数据，有0<n≤8,0<m≤8,0≤a_i​≤8。

对于 50% 数据，有0<n≤20,0<m≤20,0≤a_i≤20。

对于 100% 数据，有0<n≤100,0<m≤100,0≤a_i​≤100。

NOIP 2012 普及组 第三题

开始操作：

定义状态：f(i, j)f(i,j) 表示前 i 个数总和为 j 的方案数。

那么，易得状态转移方程：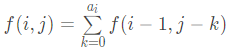

其中, k是枚举当前第 i 个数的取值。

时间复杂度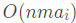：，稳得一批。

空间复杂度：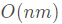

 

 可以看看大佬讲解：传送锚点

Code:

#include<bits/stdc++.h>
using namespace std;
const int mod=1e6+7;
int n,m;
int a[105];
int f[105][105];

int main()
{
    cin>>n>>m;
    for(int i=1;i<=n;i++)
        cin>>a[i];
    f[0][0]=1;
    for(int i=1;i<=n;i++)
        for(int j=0;j<=m;j++)
            for(int k=0;k<=min(a[i],j);k++)
                f[i][j]=(f[i][j]+f[i-1][j-k])%mod;
    cout<<f[n][m]<<'\n';
    return 0;
}

P3842 [TJOI2007]线段

题目描述

在一个n×n 的平面上，在每一行中有一条线段，第i行的线段的左端点是(i,L_i​)，右端点是(i,R_i​)。

你从 (1,1) 点出发，要求沿途走过所有的线段，最终到达(n,n) 点，且所走的路程长度要尽量短。

更具体一些说，你在任何时候只能选择向下走一步（行数增加 1）、向左走一步（列数减少 1）或是向右走一步（列数增加 1）。当然，由于你不能向上行走，因此在从任何一行向下走到另一行的时候，你必须保证已经走完本行的那条线段。

输入格式

第一行有一个整数 n。

以下 n 行，在第 i 行（总第 (i+1) 行）的两个整数表示 L_i​ 和 R_i​。

输出格式

仅包含一个整数，你选择的最短路程的长度。

输入输出样例

输入 #1复制

6
2 6
3 4
1 3
1 2
3 6
4 5

输出 #1复制

24

说明/提示

我们选择的路线是

 (1, 1) (1, 6)
 (2, 6) (2, 3)
 (3, 3) (3, 1)
 (4, 1) (4, 2)
 (5, 2) (5, 6)
 (6, 6) (6, 4) (6, 6)

不难计算得到，路程的总长度是 2424。

对于 100\%100% 的数据中，n≤2×10⁴，1≤L_i≤R_i​≤n。

 又是DP。

f[i][0]表示走完第i行且停在第i行的左端点最少用的步数

f[i][1]同理，停在右端点的最少步数。

那么转移就很简单了，走完当前行且停到左端点，那么一定是从右端点过来的，那么从上一行左端点转移的话就是

f[i][0]=abs(上一行左端点的坐标-本行右端点的坐标+本行线段长度)

从上一行右端点转移同理。 不需要什么判断。边界f[1][0]=r[1]+r[1]-l[1]-1,f[1][1]=r[1]-1，然后直接搞就行了，时间复杂度O(n)。

注：abs(i)是求i的绝对值。

Code:

#include<bits/stdc++.h>
using namespace std;
const int N=2e4+5;
int n;
int l[N],r[N];
int f[N][2];

int main()
{
    cin>>n;
    for(int i=1;i<=n;i++)
        cin>>l[i]>>r[i];
    f[1][0]=r[1]+r[1]-l[1]-1;
    f[1][1]=r[1]-1;
    for(int i=2;i<=n;i++)
    {
        f[i][0]=min(f[i-1][0]+abs(l[i-1]-r[i])+r[i]-l[i]+1,f[i-1][1]+abs(r[i-1]-r[i])+r[i]-l[i]+1);
        f[i][1]=min(f[i-1][0]+abs(l[i-1]-l[i])+r[i]-l[i]+1,f[i-1][1]+abs(r[i-1]-l[i])+r[i]-l[i]+1);
    }
    cout<<min(f[n][0]+n-l[n],f[n][1]+n-r[n]);
}

P1064 [NOIP2006 提高组] 金明的预算方案

题目描述

金明今天很开心，家里购置的新房就要领钥匙了，新房里有一间金明自己专用的很宽敞的房间。更让他高兴的是，妈妈昨天对他说：“你的房间需要购买哪些物品，怎么布置，你说了算，只要不超过 n 元钱就行”。今天一早，金明就开始做预算了，他把想买的物品分为两类：主件与附件，附件是从属于某个主件的，下表就是一些主件与附件的例子：

主件	附件
电脑	打印机，扫描仪
书柜	图书
书桌	台灯，文具
工作椅	无

如果要买归类为附件的物品，必须先买该附件所属的主件。每个主件可以有 0 个、1 个或 2 个附件。每个附件对应一个主件，附件不再有从属于自己的附件。金明想买的东西很多，肯定会超过妈妈限定的 n 元。于是，他把每件物品规定了一个重要度，分为 5 等：用整数1∼5 表示，第 5 等最重要。他还从因特网上查到了每件物品的价格（都是 10 元的整数倍）。他希望在不超过 n 元的前提下，使每件物品的价格与重要度的乘积的总和最大。

设第 j 件物品的价格为 v_j​，重要度为w_j​，共选中了 k 件物品，编号依次为 j₁​,j₂​,…,j_k，则所求的总和为：v_j1​​×w_j1+v_j2×w_j2​​+⋯+v_jk​​×w_jk。

请你帮助金明设计一个满足要求的购物单。

输入格式

第一行有两个整数，分别表示总钱数 n 和希望购买的物品个数 m。

第 2 到第 (m+1) 行，每行三个整数，第(i+1) 行的整数 v_i，p_i，q_i 分别表示第 i 件物品的价格、重要度以及它对应的的主件。如果q_i=0，表示该物品本身是主件。

输出格式

输出一行一个整数表示答案。

输入输出样例

输入 #1复制

1000 5
800 2 0
400 5 1
300 5 1
400 3 0
500 2 0

输出 #1复制

2200

说明/提示

数据规模与约定

对于全部的测试点，保证 1≤n≤3.2×10⁴，1≤m≤60，0≤v_i≤10⁴，1≤p_i​≤5，0≤q_i≤m，答案不超过 2×10⁵。

日常水题解：

这题乍一看：又是主件又是附件的，感觉好复杂。再一看：附件数量不超过2，物品个数才不到60。

感觉自己能行，不就是DP吗，搞得好像谁不会DP一样。

由于买了主件才买附件且附件数量不超过2，我们不妨直接将主件和附件捆绑成一组。

对于有两个附件的组别，无非只有以下4种情况：

  1.只买主件

  2.主件+附件1。

  3.主件+附件2

  4.主件+附件1+附件2

而对于有一个附件的组别，则没有情况3和情况4；对于只有主件的组别，则只有情况1。

故而直接设w[i][j]表示组别 i 的第 j 种情况的价格，u[i][j]表示则表示对应w与重要度的乘积，sl[i]表示组别 i 的情况数量，tot表示总的组别数量。

将这些信息预处理出来，然后就可以做DP了。

DP过程很简单，从每个组别挑选0到1种情况，总价格不超过m而u最大，典型的分组背包。

Code:

#include<bits/stdc++.h>
using namespace std;
int n,m,tot;
int v[65],p[65],q[65],z[65],sl[65];
int f[32005],w[65][65],u[65][65];

int main()
{
    cin>>n>>m;
    for(int i=1;i<=m;i++)
    {
        cin>>v[i]>>p[i]>>q[i];
        if(q[i]==0)
        {
            w[++tot][++sl[tot]]=v[i];
            u[tot][sl[tot]]=v[i]*p[i];
            z[i]=tot;
        }
    }
    for(int i=1;i<=m;i++)
    {
        if(q[i]!=0)
        {
            int x=z[q[i]];
            w[x][++sl[x]]=v[i]+w[x][1];
            u[x][sl[x]]=v[i]*p[i]+u[x][1];
            if(sl[x]==3)
            {
                w[x][++sl[x]]=w[x][2]+w[x][3]-w[x][1];
                u[x][sl[x]]=u[x][2]+u[x][3]-u[x][1];
            }
        }
    }
    for(int i=1;i<=tot;i++)
        for(int j=n;j>=0;j-=10)
            for(int k=1;k<=sl[i];k++)
                if(j>=w[i][k])
                    f[j]=max(f[j],f[j-w[i][k]]+u[i][k]);
    cout<<f[n]<<endl;
}

P2392 kkksc03考前临时抱佛脚

题目背景

kkksc03 的大学生活非常的颓废，平时根本不学习。但是，临近期末考试，他必须要开始抱佛脚，以求不挂科。

题目描述

这次期末考试，kkksc03 需要考 4 科。因此要开始刷习题集，每科都有一个习题集，分别有 s₁​,s₂​,s₃​,s₄​ 道题目，完成每道题目需要一些时间，可能不等（A₁,A₂​,…,A_s1，B₁,B₂,…,B_s2​​，C₁​,C₂,…,C_s3​​，D₁​,D₂​,…,D_s4）。

kkksc03 有一个能力，他的左右两个大脑可以同时计算 2 道不同的题目，但是仅限于同一科。因此，kkksc03 必须一科一科的复习。

由于 kkksc03 还急着去处理洛谷的 bug，因此他希望尽快把事情做完，所以他希望知道能够完成复习的最短时间。

输入格式

本题包含 5 行数据：第 1 行，为四个正整数 s₁,s₂,s₃​,s₄。

第 2 行，为 A₁​,A₂,…,A_s1​​ 共 s₁​ 个数，表示第一科习题集每道题目所消耗的时间。

第 3 行，为 B₁,B₂​,…,B_s2 共 s₂ 个数。

第 4 行，为 C₁,C₂​,…,C_s3 共 s₃​ 个数。

第 5 行，为 D₁​,D₂,…,D_s4​​ 共 s₄​ 个数，意思均同上。

输出格式

输出一行,为复习完毕最短时间。

输入输出样例

输入 #1复制

1 2 1 3		
5
4 3
6
2 4 3

输出 #1复制

20

说明/提示

1≤s₁,s₂​,s₃​,s₄≤20。

1≤A₁​,A₂​,…,A_s1​​,B₁​,B₂​,…,B_s2​​,C₁​,C₂​,…,C_s3​​,D₁​,D₂​,…,D_s4​​≤60。

人都要做麻了呀：

首先理清思路:

• 1.所求最少时间即4科最少时间的总和

• 2.因为kkksc03是双核,故单科最少总时间分配给两核的时间应尽量相同

• 3.故:以单科总时间一半为界限,做0/1背包是所花时间尽量靠近与half

• 4.背包结束后 dp[half]总是小于等于tot-dp[half],应累加较大值即后式

详见：传送锚点

Code：

#include<bits/stdc++.h>
using namespace std;
const int N=1e5+5;
int tot,ans;
int a[5],b[5][21];
int f[N];

int main()
{
    for(int i=1;i<5;i++)
        cin>>a[i];
    for(int i=1;i<5;i++)
    {
        memset(f,0,sizeof(f));
        tot=0;
        for(int j=1;j<=a[i];j++)
        {
            cin>>b[i][j];
            tot+=b[i][j];
        }
        for(int j=1;j<=a[i];j++)
            for(int k=tot/2;k>=b[i][j];k--)
                f[k]=max(f[k],f[k-b[i][j]]+b[i][j]);
        ans+=tot-f[tot>>1];
    }
    cout<<ans<<'\n';
}