[UOJ#221][BZOJ4652][Noi2016]循环之美

[UOJ#221][BZOJ4652][Noi2016]循环之美

试题描述

牛牛是一个热爱算法设计的高中生。在他设计的算法中，常常会使用带小数的数进行计算。牛牛认为，如果在 k 进制下，一个数的小数部分是纯循环的，那么它就是美的。现在，牛牛想知道：对于已知的十进制数 n 和 m，在 k 进制下，有多少个数值上互不相等的纯循环小数，可以用分数 x/y 表示,其中 1≤x≤n,1≤y≤m，且 x,y是整数。一个数是纯循环的，当且仅当其可以写成以下形式：a.c1˙c2c3…cp-1cp˙其中，a 是一个整数，p≥1；对于 1≤i≤p，ci是 kk 进制下的一位数字。例如，在十进制下，0.45454545……=0.4˙5˙是纯循环的，它可以用 5/11、10/22 等分数表示；在十进制下，0.1666666……=0.16˙则不是纯循环的，它可以用 1/6 等分数表示。需要特别注意的是，我们认为一个整数是纯循环的，因为它的小数部分可以表示成 0 的循环或是 k?1 的循环；而一个小数部分非 0 的有限小数不是纯循环的。
提示

这部分将提供一个将分数化为对应的小数的方法，如果你已经熟悉这个方法，你不必阅读本提示。

分数可以通过除法，用分子除以分母化为对应的小数。有些分数在除法过程中无法除尽,这样的分数在不断进行的除法过程中余数一定会重复出现。从商数的个位所对应的余数起，设第一次重复出现的余数前两次出现的位置所对应的商数位分别是小数点后第 aa 位和小数点后第 bb 位（特殊地：如果其中一个对应的商数位是个位，则认为 a=0；不妨设 a<b），则其循环部分可以用小数点后第 a+1 位到小数点后第 b 位的循环来表示。

例如：在十进制下，将 5/11 转化为小数时，个位开始的商数依次为 4,5,4,…，对应的余数分别为 6,5,6,…。余数第一次重复出现的位置是个位和小数点后第 2 位,那么 a=0,b=2 即其循环部分可以用小数点第 1 位到第 3 位来表示。表示为：5/11=0.45454545…=0.4˙5˙。

在十进制下，将 1/6 转化为小数时,个位开始的商数依次为 1,6,6,…，对应的余数分别为 4,4,4,…。余数第一次重复出现的位置是小数点后第 1 位和小数点后第 2 位,即其循环部分可以用小数点后第 2 位来表示。表示为：16=0.1666……=0.16˙。

需要注意的是：商数重复出现并不代表进入了循环节。

输入

只有一行，包含三个十进制数N,M,K意义如题所述,保证 1≤n≤10^9,1≤m≤10^9,2≤k≤2000

输出

一行一个整数，表示满足条件的美的数的个数。

输入示例

2 6 10

输出示例

4

数据规模及约定

见“输入”

题解

根据它的提示，我们可以列一列式子：（令商第 i 位后的余数为 pi）

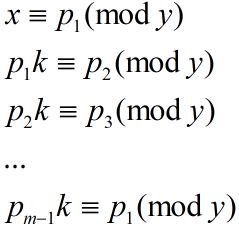
联立得到

又有 (x, y) = 1，所以得到 km mod y = 1，即 (k, y) = 1。

那么现在题目就是在求：

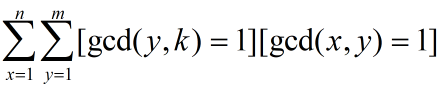
纯暴力 24 分可以拿到了。

接下来，学习了莫比乌斯反演，我们知道它可以变形

交换一下枚举顺序，得到

那么如果最右边那个Σ能够 O(1) 得到，枚举 d 即可 O(nlogk) 求解，那个Σ求法如下

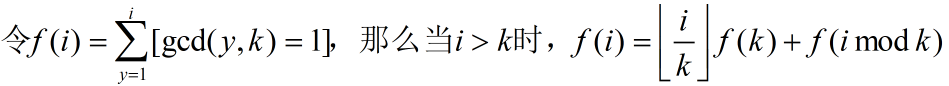
所以我们只需要预处理出 i = 1, 2, ..., k 时 f(i) 的值即可。至此我们拿到了 84 分。

#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <cctype>
#include <algorithm>
using namespace std;

int read() {
	int x = 0, f = 1; char c = getchar();
	while(!isdigit(c)){ if(c == '-') f = -1; c = getchar(); }
	while(isdigit(c)){ x = x * 10 + c - '0'; c = getchar(); }
	return x * f;
}

#define maxn 20000001
#define maxk 2010
#define LL long long

bool vis[maxn];
int cp, prime[maxn], mu[maxn];
void init() {
	mu[1] = 1;
	for(int i = 2; i < maxn; i++) {
		if(!vis[i]) prime[++cp] = i, mu[i] = -1;
		for(int j = 1; i * prime[j] < maxn && j <= cp; j++) {
			vis[i*prime[j]] = 1;
			if(i % prime[j] == 0){ mu[i*prime[j]] = 0; break; }
			mu[i*prime[j]] = -mu[i];
		}
	}
	return ;
}

int gcd(int a, int b) { return b ? gcd(b, a % b) : a; }

int f[maxk];
int calc(int n, int k) {
	return n / k * f[k] + f[n%k];
}

int main() {
	init();
	
	int n = read(), m = read(), k = read();
	for(int i = 1; i <= k; i++) f[i] = f[i-1] + (gcd(i, k) == 1);
	
	LL sum = 0;
	for(int d = 1; d <= n; d++) if(gcd(d, k) == 1) sum += (LL)mu[d] * (n / d) * calc(m / d, k);
	printf("%lld\n", sum);
	
	return 0;
}

接着推式子

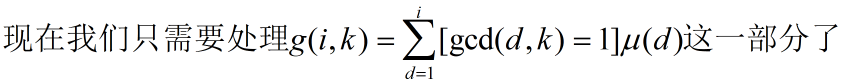
如果我们能快速求出 g(i, k) 的值，那么可以给后面 [n / d] 以及 f([m / d]) 的值分成 2(sqrt(n) + sqrt(m)) 类并最终高效地求得答案。

考虑 k 的一个质因数 p，那么 k = ptq，[gcd(d,k)=1] 的部分 = [gcd(d,q)=1] 的部分 - [gcd(d,p)>1][gcd(d,q)=1]的部分，所以得到

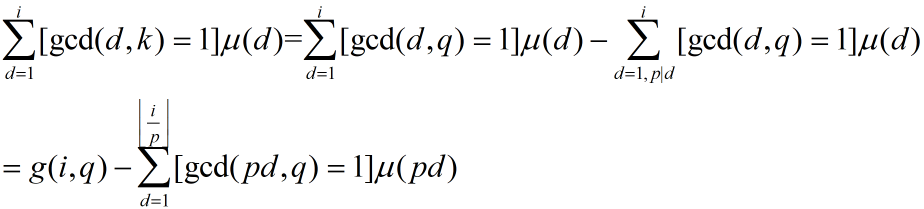
显然 [gcd(pd,q)=1] = [gcd(p,q)=1][gcd(d,q)=1] = [gcd(d,q)=1]

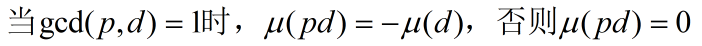
又因为 [gcd(d,q)=1][gcd(d,p)=1] = [gcd(d,pq)=1]，所以，把上式接着变化

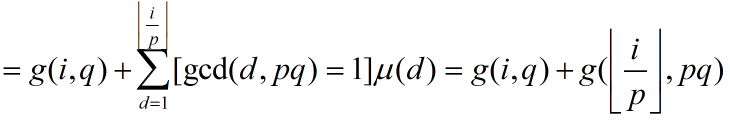
这样，我们就可以递归求 g(i, k) 了，每次要么 k 除掉一个它的质因数（除干净），要么 i 变成 [i / p]，所以状态数会非常少。

递归边界：i = 0 时 g(i, k) = 0；k = 1 时 g(i, k) 就是莫比乌斯函数的前缀和，学习了杜教筛，就迎刃而解了。

#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <cctype>
#include <algorithm>
using namespace std;

int read() {
	int x = 0, f = 1; char c = getchar();
	while(!isdigit(c)){ if(c == '-') f = -1; c = getchar(); }
	while(isdigit(c)){ x = x * 10 + c - '0'; c = getchar(); }
	return x * f;
}

#define maxn 1000001
#define maxk 2010
#define MOD 1000007
#define LL long long
#define oo 2147483647

bool vis[maxn];
int cp, prime[maxn], mu[maxn], smu[maxn];
void init() {
	mu[1] = 1; smu[1] = 1;
	for(int i = 2; i < maxn; i++) {
		if(!vis[i]) prime[++cp] = i, mu[i] = -1;
		for(int j = 1; i * prime[j] < maxn && j <= cp; j++) {
			vis[i*prime[j]] = 1;
			if(i % prime[j] == 0){ mu[i*prime[j]] = 0; break; }
			mu[i*prime[j]] = -mu[i];
		}
		smu[i] = smu[i-1] + mu[i];
	}
	return ;
}

int gcd(int a, int b) { return b ? gcd(b, a % b) : a; }

int f[maxk];
int calc(int n, int k) {
	return n / k * f[k] + f[n%k];
}

struct Hash {
	int ToT, head[MOD], nxt[maxn], num[maxn], num2[maxn], val[maxn];
	Hash() { ToT = 0; memset(head, 0, sizeof(head)); }
	void Insert(int x, int v) {
		int u = x % MOD;
		nxt[++ToT] = head[u]; num[ToT] = x; val[ToT] = v; head[u] = ToT;
		return ;
	}
	void Insert2(int x1, int x2, int v) {
		int u = ((LL)x1 * 233 + x2) % MOD;
		nxt[++ToT] = head[u]; num[ToT] = x1; num2[ToT] = x2; val[ToT] = v; head[u] = ToT;
		return ;
	}
	int Find(int x) {
		int u = x % MOD;
		for(int e = head[u]; e; e = nxt[e]) if(num[e] == x) return val[e];
		return 0;
	}
	int Find2(int x1, int x2) {
		int u = ((LL)x1 * 233 + x2) % MOD;
		for(int e = head[u]; e; e = nxt[e]) if(num[e] == x1 && num2[e] == x2) return val[e];
		return oo;
	}
} hh, hh2;

int getsum(int n) {
	if(n < maxn) return smu[n];
	if(hh.Find(n)) return hh.Find(n);
	int sum = 1;
	for(int i = 2, lst; i <= n; i = lst + 1) {
		lst = n / (n / i);
		sum -= getsum(n / i) * (lst - i + 1);
	}
	hh.Insert(n, sum);
	return sum;
}

int fir_p[maxk], lst_q[maxk];
int Find(int n, int k) {
	if(!n) return 0;
	if(k == 1) return getsum(n);
	if(hh2.Find2(n, k) < oo) return hh2.Find2(n, k);
	int p = fir_p[k], q = lst_q[k];
	int tmp = Find(n, q) + Find(n / p, p * q);
	hh2.Insert2(n, k, tmp);
	return tmp;
}

int main() {
	init();
	
	int n = read(), m = read(), k = read();
	for(int i = 1; i <= k; i++) f[i] = f[i-1] + (gcd(i, k) == 1);
	
	for(int K = 2; K <= k; K++)
		for(int i = 1; i <= cp; i++) if(K % prime[i] == 0) {
			fir_p[K] = prime[i];
			lst_q[K] = K; while(lst_q[K] % fir_p[K] == 0) lst_q[K] /= fir_p[K];
			break;
		}
	LL sum = 0;
	for(int i = 1, lst; i <= min(n, m); i = lst + 1) {
		lst = min(n / (n / i), m / (m / i));
		sum += (LL)(Find(lst, k) - Find(i - 1, k)) * (n / i) * calc(m / i, k);
	}
	printf("%lld\n", sum);
	
	return 0;
}

顺便补一下杜教筛的核心公式：

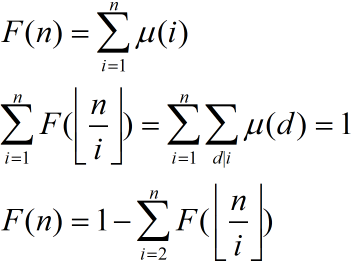
然后我们就可以通过对 [n / i] 的值分类递归求出 F(n) 了（第二行第一个等号画画表理解吧。。。）

其实杜教筛适用于所有狄利克雷卷积非常好算的数论函数。

posted @ 2017-06-28 20:02  xjr01  阅读(325)  评论(0)  编辑  收藏  举报