HDU 4421 2-SAT
Bit Magic
Problem Description
Yesterday, my teacher taught me about bit operators: and (&), or (|), xor (^). I generated a number table a[N], and wrote a program to calculate the matrix table b[N][N] using three kinds of bit operator. I thought my achievement would get teacher's attention.
The key function is the code showed below.
![]()
There is no doubt that my teacher raised lots of interests in my work and was surprised to my talented programming skills. After deeply thinking, he came up with another problem: if we have the matrix table b[N][N] at first, can you check whether corresponding number table a[N] exists?
The key function is the code showed below.
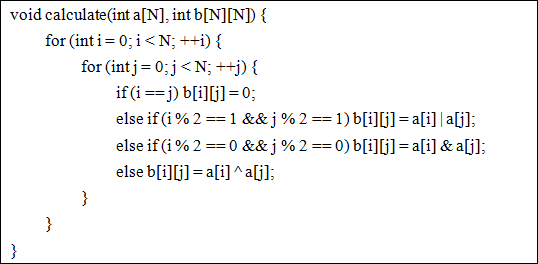
There is no doubt that my teacher raised lots of interests in my work and was surprised to my talented programming skills. After deeply thinking, he came up with another problem: if we have the matrix table b[N][N] at first, can you check whether corresponding number table a[N] exists?
Input
There are multiple test cases.
For each test case, the first line contains an integer N, indicating the size of the matrix. (1 <= N <= 500).
The next N lines, each line contains N integers, the jth integer in ith line indicating the element b[i][j] of matrix. (0 <= b[i][j] <= 2 31 - 1)
For each test case, the first line contains an integer N, indicating the size of the matrix. (1 <= N <= 500).
The next N lines, each line contains N integers, the jth integer in ith line indicating the element b[i][j] of matrix. (0 <= b[i][j] <= 2 31 - 1)
Output
For each test case, output "YES" if corresponding number table a[N] exists; otherwise output "NO".
Sample Input
2 0 4 4 0 3 0 1 24 1 0 86 24 86 0
Sample Output
YES NO
题意:给定一个矩阵b,看是否存在一个数组a,使得满足条件。
解题思路:判断b数组每一位,然后根据矛盾关系建图,2-sat判定,做31次2-sat判定即可。
代码:
#include<iostream>
#include<stdio.h>
#include<string.h>
#include<algorithm>
#include<string>
using namespace std;
struct node
{
int to,next;
}edge[9000000];
int head[300000],tol,low[300000],dfn[300000],indexx,Stack[3000000],instack[300000],belong[300000],scc,top,m,n,s[600][600];
void add(int u,int v)
{
edge[tol].to=v;
edge[tol].next=head[u];
head[u]=tol++;
}
void tarjin(int u)
{
low[u]=dfn[u]=++indexx;
Stack[top++]=u;instack[u]=1;
int i,v;
for(int i=head[u];i!=-1;i=edge[i].next)
{
v=edge[i].to;
if(!dfn[v])
{
tarjin(v);
if(low[u]>low[v])low[u]=low[v];
}
else if(instack[v]&&low[u]>dfn[v])low[u]=dfn[v];
}
if(low[u]==dfn[u])
{
scc++;
do
{
v=Stack[--top];
instack[v]=0;
belong[v]=scc;
}while(u!=v);
}
}
int solve()
{
int i,j,u,v;
memset(belong,0,sizeof(belong));
memset(dfn,0,sizeof(dfn));
memset(instack,0,sizeof(instack));
indexx=scc=top=0;
for(i=0;i<2*n;i++)if(!dfn[i])tarjin(i);
for(i=0;i<n;i++)if(belong[2*i]==belong[2*i+1])return 0;
return 1;
}
bool judge()
{
int i,j;
for(i=0;i<n;i++)
for(j=0;j<n;j++)
{
if(i==j)if(s[i][j])return 0;
else
{
if(s[i][j]!=s[j][i])return 0;
}
}
return 1;
}
int main()
{
int i,j,k,T,t;
while(~scanf("%d",&n))
{
for(i=0;i<n;i++)
for(j=0;j<n;j++)scanf("%d",&s[i][j]);
if(!judge())
{
puts("NO");continue;
}
int flag=1;
for(k=0;flag&&k<31;k++)
{
memset(head,-1,sizeof(head));tol=0;
for(i=0;i<n;i++)
for(j=i+1;j<n;j++)
{
if(i%2&&j%2)
{
if((s[i][j]>>k)&1)
{
add(2*i+1,2*j);
add(2*j+1,2*i);
}
else
{
add(2*i,2*i+1);
add(2*j,2*j+1);
}
}
else if(i%2==0&&j%2==0)
{
if((s[i][j]>>k)&1)
{
add(2*i+1,2*i);
add(2*j+1,2*j);
}
else
{
add(2*i,2*j+1);
add(2*j,2*i+1);
}
}
else
{
if((s[i][j]>>k)&1)
{
add(2*i,2*j+1);
add(2*i+1,2*j);
add(2*j,2*i+1);
add(2*j+1,2*i);
}
else
{
add(2*i,2*j);
add(2*i+1,2*j+1);
add(2*j,2*i);
add(2*j+1,2*i+1);
}
}
}
if(!solve())flag=0;
}
if(flag)puts("YES");else puts("NO");
}
return 0;
}
#include<stdio.h>
#include<string.h>
#include<algorithm>
#include<string>
using namespace std;
struct node
{
int to,next;
}edge[9000000];
int head[300000],tol,low[300000],dfn[300000],indexx,Stack[3000000],instack[300000],belong[300000],scc,top,m,n,s[600][600];
void add(int u,int v)
{
edge[tol].to=v;
edge[tol].next=head[u];
head[u]=tol++;
}
void tarjin(int u)
{
low[u]=dfn[u]=++indexx;
Stack[top++]=u;instack[u]=1;
int i,v;
for(int i=head[u];i!=-1;i=edge[i].next)
{
v=edge[i].to;
if(!dfn[v])
{
tarjin(v);
if(low[u]>low[v])low[u]=low[v];
}
else if(instack[v]&&low[u]>dfn[v])low[u]=dfn[v];
}
if(low[u]==dfn[u])
{
scc++;
do
{
v=Stack[--top];
instack[v]=0;
belong[v]=scc;
}while(u!=v);
}
}
int solve()
{
int i,j,u,v;
memset(belong,0,sizeof(belong));
memset(dfn,0,sizeof(dfn));
memset(instack,0,sizeof(instack));
indexx=scc=top=0;
for(i=0;i<2*n;i++)if(!dfn[i])tarjin(i);
for(i=0;i<n;i++)if(belong[2*i]==belong[2*i+1])return 0;
return 1;
}
bool judge()
{
int i,j;
for(i=0;i<n;i++)
for(j=0;j<n;j++)
{
if(i==j)if(s[i][j])return 0;
else
{
if(s[i][j]!=s[j][i])return 0;
}
}
return 1;
}
int main()
{
int i,j,k,T,t;
while(~scanf("%d",&n))
{
for(i=0;i<n;i++)
for(j=0;j<n;j++)scanf("%d",&s[i][j]);
if(!judge())
{
puts("NO");continue;
}
int flag=1;
for(k=0;flag&&k<31;k++)
{
memset(head,-1,sizeof(head));tol=0;
for(i=0;i<n;i++)
for(j=i+1;j<n;j++)
{
if(i%2&&j%2)
{
if((s[i][j]>>k)&1)
{
add(2*i+1,2*j);
add(2*j+1,2*i);
}
else
{
add(2*i,2*i+1);
add(2*j,2*j+1);
}
}
else if(i%2==0&&j%2==0)
{
if((s[i][j]>>k)&1)
{
add(2*i+1,2*i);
add(2*j+1,2*j);
}
else
{
add(2*i,2*j+1);
add(2*j,2*i+1);
}
}
else
{
if((s[i][j]>>k)&1)
{
add(2*i,2*j+1);
add(2*i+1,2*j);
add(2*j,2*i+1);
add(2*j+1,2*i);
}
else
{
add(2*i,2*j);
add(2*i+1,2*j+1);
add(2*j,2*i);
add(2*j+1,2*i+1);
}
}
}
if(!solve())flag=0;
}
if(flag)puts("YES");else puts("NO");
}
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号