HDU 3594 仙人掌图

Cactus

Problem Description

1. It is a Strongly Connected graph.
2. Each edge of the graph belongs to a circle and only belongs to one circle.
We call this graph as CACTUS.



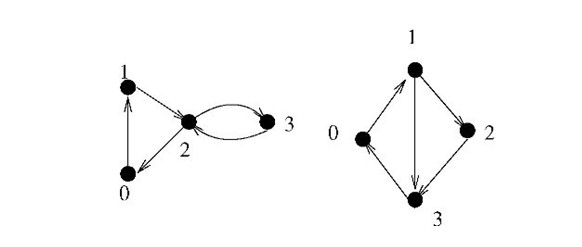
There is an example as the figure above. The left one is a cactus, but the right one isn’t. Because the edge (0, 1) in the right graph belongs to two circles as (0, 1, 3) and (0, 1, 2, 3).

 

Input

The input consists of several test cases. The first line contains an integer T (1<=T<=10), representing the number of test cases.
For each case, the first line contains a integer n (1<=n<=20000), representing the number of points.
The following lines, each line has two numbers a and b, representing a single-way edge (a->b). Each case ends with (0 0).
Notice: The total number of edges does not exceed 50000.

 

Output

For each case, output a line contains “YES” or “NO”, representing whether this graph is a cactus or not.

 

Sample Input

2
4
0 1
1 2
2 0
2 3
3 2
0 0
4
0 1
1 2
2 3
3 0
1 3
0 0

 

Sample Output

YES
NO

题意：判断一个图是否为仙人掌图。

其中，仙人掌图满足两个条件：

（1） 为强连通图，即只有一个强连通分量。

（2）每条边有且仅属于一个有向环。

解题思路：tarjin缩点，在缩点的时候，如果出现两个连通分量，则直接跳出，返回NO，遇到一个点在栈内，就从当前访问的点沿着父亲，一路往回，统计每条边出现的次数，只要出现有一条边出现两次，就直接返回NO，否则返回YES。

代码：

#include<iostream>
#include<stdio.h>
#include<algorithm>
#include<string.h>
#include<string>
using namespace std;
const int maxn=200000;
int head[maxn],tol,scc,top,indexx,low[maxn],instack[maxn],Stack[maxn],flag[maxn],ok,n,fa[maxn],dfn[maxn];
struct node
{
        int to,next;
}edge[10*maxn];
void  add(int u,int v)
{
        edge[tol].to=v;
        edge[tol].next=head[u];
        head[u]=tol++;
}
void sign(int v,int x)
    {
        while(fa[x]!=v)
        {
            flag[x]++;
            if(flag[x]>1)
            {
                ok=false;
                return ;
            }
            x=fa[x];
        }
    }
void tarjin(int u)
{
        low[u]=dfn[u]=++indexx;
        Stack[top++]=u;instack[u]=1;
        int i,v;
        for(int i=head[u];i!=-1;i=edge[i].next)
        {
                v=edge[i].to;
                if(!dfn[v])
                {
                        fa[v]=u;
                        tarjin(v);
                        if(low[u]>low[v])low[u]=low[v];
                }
                else if(instack[v])
                {
                        if(low[u]>dfn[v])low[u]=dfn[v];
                        sign(v,u);
                        if(ok==0)return;
                }
        }
        if(low[u]==dfn[u])
        {
                scc++;
                if(scc>1)
                {
                        ok=0;
                        return;
                }
                do
                {
                        v=Stack[--top];
                        instack[v]=0;
                }while(u!=v);
        }
}

int main()
{
        int i,j,k,T,m;
        scanf("%d",&T);
        while(T--)
        {
                scanf("%d",&n);
                memset(head,-1,sizeof(head));tol=0;
                while(~scanf("%d%d",&i,&j))
                {
                        if(i+j==0)break;
                        add(i,j);
                }
                memset(dfn,0,sizeof(dfn));
                memset(instack,0,sizeof(instack));
                memset(fa,0,sizeof(fa));
                memset(flag,0,sizeof(flag));
                ok=1;
                indexx=scc=top=0;
                for(i=0;i<n;i++)if(ok&&!dfn[i])tarjin(i);
              //  cout<<scc<<endl;
                if(ok)puts("YES");
                else puts("NO");
        }
        return 0;
}