POJ 2296 二分+2-SAT

                                                                                         Map Labeler

Time Limit: 1000MS		Memory Limit: 65536K
Total Submissions: 1408		Accepted: 456

Description

Map generation is a difficult task in cartography. A
vital part of such task is automatic labeling of the cities in a map; where for
each city there is text label to be attached to its location, so that no two
labels overlap. In this problem, we are concerned with a simple case of
automatic map labeling.

Assume that each city is a point on the plane,
and its label is a text bounded in a square with edges parallel to x and y axis.
The label of each city should be located such that the city point appears
exactly in the middle of the top or bottom edges of the label. In a good
labeling, the square labels are all of the same size, and no two labels overlap,
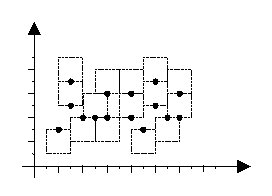
although they may share one edge. Figure 1 depicts an example of a good labeling
(the texts of the labels are not shown.)

Given the coordinates of all
city points on the map as integer values, you are to find the maximum label size
(an integer value) such that a good labeling exists for the map.

Input

The first line contains a single integer t (1 <= t
<= 10), the number of test cases. Each test case starts with a line
containing an integer m (3 ≤ m ≤ 100), the number of cities followed by m lines
of data each containing a pair of integers; the first integer (X) is the x and
the second one (Y) is the y coordinates of one city on the map (-10000 ≤X, Y≤
10000). Note that no two cities have the same (x, y) coordinates.

Output

The output will be one line per each test case
containing the maximum possible label size (an integer value) for a good
labeling.

Sample Input

1
6
1 1
2 3
3 2
4 4
10 4
2 5

Sample Output

2

题意：不解释。

解题思路：二分+2-SAT

代码：
#include<iostream>
#include<stdio.h>
#include<string.h>
#include<algorithm>
#include<map>
#include<string>
#include<vector>
#include<stack>
#include<math.h>
#include<iomanip>
using namespace std;
const int maxn=210;
const int maxm=1000000;
struct point
{
        int x,y;
}p[maxn];
int head[maxn],tol,low[maxn],dfn[maxn],Stack[maxn],instack[maxn],belong[maxn],scc,top,indexx,n;
struct node
{
        int next,to;
}edge[maxm];
void add(int u,int v)
{
        edge[tol].next=head[u];
        edge[tol].to=v;
        head[u]=tol++;
}
void tarjin(int u)
{
        low[u]=dfn[u]=++indexx;
        Stack[top++]=u;instack[u]=1;
        int i,v;
        for(i=head[u];i!=-1;i=edge[i].next)
        {
                v=edge[i].to;
                if(!dfn[v])
                {
                        tarjin(v);
                        if(low[u]>low[v])low[u]=low[v];
                }
                else if(instack[v]&&low[u]>dfn[v])low[u]=dfn[v];
        }
        if(low[u]==dfn[u])
        {
                scc++;
                do
                {
                        v=Stack[--top];
                        instack[v]=0;
                        belong[v]=scc;
                }while(u!=v);
        }
}
int solve(int r)
{
        memset(head,-1,sizeof(head));
        memset(instack,0,sizeof(instack));
        memset(dfn,0,sizeof(dfn));
        memset(belong,0,sizeof(belong));
        indexx=scc=top=0;tol=0;
        int i,j;
        for(i=0;i<n;i++)
        for(j=i+1;j<n;j++)
        {
               if(abs(p[i].x-p[j].x)>=r)continue;
               if(p[i].y==p[j].y)
               {
                       add(2*i,2*j+1);
                       add(2*i+1,2*j);
                       add(2*j,2*i+1);
                       add(2*j+1,2*i);
               }
               else if(p[i].y>p[j].y)
               {
                     if(p[i].y-p[j].y>=2*r)continue;
                     if(p[i].y-p[j].y<r)
                     {
                             add(2*i+1,2*i);
                             add(2*j,2*j+1);
                     }
                     else
                     {
                             add(2*i+1,2*j+1);
                             add(2*j,2*i);
                     }
               }
               else
               {
                       if(p[j].y-p[i].y>=2*r)continue;
                       if(p[j].y-p[i].y<r)
                       {
                               add(2*j+1,2*j);
                               add(2*i,2*i+1);
                       }
                       else
                       {
                               add(2*j+1,2*i+1);
                               add(2*i,2*j);
                       }
               }
        }
        //cout<<tol<<endl;
        for(i=0;i<2*n;i++)if(!dfn[i])tarjin(i);
        for(i=0;i<n;i++)if(belong[2*i]==belong[2*i+1])return 0;
        return 1;
}
int fun()
{
       char ch;
       int flag=1,a=0;
       while(ch=getchar())
       {
              if((ch>='0'&&ch<='9')||ch=='-')break;
       }
       if(ch=='-')flag=-1;
       else a=ch-'0';
       while(ch=getchar())
       {
              if(ch>='0'&&ch<='9')a=10*a+ch-'0';
              else break;
       }
       return flag*a;
}

int main()
{
        int i,j,k,m,T;
        T=fun();
        while(T--)
        {
                n=fun();
                for(i=0;i<n;i++)
                {
                        p[i].x=fun();
                        p[i].y=fun();
                }
                int left=0,right=80000,mid;
                int ans;
                while(left<right)
                {
                        mid=(left+right+1)/2;
                        i=solve(mid);
                        if(!i)right=mid-1;
                        else left=mid;
                }
               // while(solve(left)==0)left--;
                printf("%d\n",left);
               // cout<<solve(1)<<endl;
        }
        return 0;
}