第三次作业：小批量梯度下降

一.作业要求

问题一：

• 使用minibatch的方式进行梯度下降
• 采用随机选取数据的方式
• batch size分别选择5，10，15进行运行

复习讲过的课程并回答关于损失函数的 2D 示意图的问题：

• 问题2：为什么是椭圆而不是圆？如何把这个图变成一个圆？
• 问题3：为什么中心是个椭圆区域而不是一个点？

项目	内容
这个作业属于哪个课程	人工智能实战
我在这个课程的目标是	将人工智能技术与本专业知识联系
这个作业在哪个具体方面帮助我实现目标	通过代码实现加深对SGD以及小批量梯度下降的理解
作业正文	链接

二、解决方法

在示例代码的基础上进行一些修改添加，实现随机数据选取

1. 随机选取数据的方式

def GetRandomBatchSamples(X,Y,batch_size,iteration):
    rnd_idx = np.random.permutation(len(X[0]))
    num_feature = X.shape[0]
    start = iteration * batch_size
    end = start + batch_size
    batch_x=[]
    batch_y=[]
    for i in range(batch_size):
        batch_x.append(X[0][rnd_idx[i]])
        batch_y.append(Y[0][rnd_idx[i]])
    batch_x=np.array(batch_x).reshape(num_feature,batch_size)
    batch_y=np.array(batch_y).reshape(num_feature,batch_size)
    return batch_x, batch_y

三、结果展示

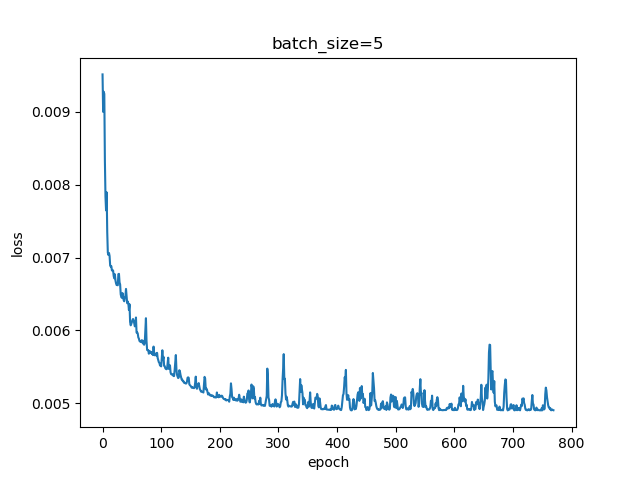
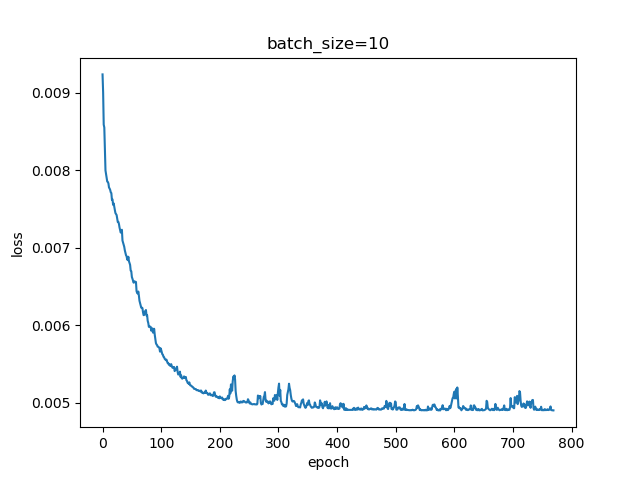
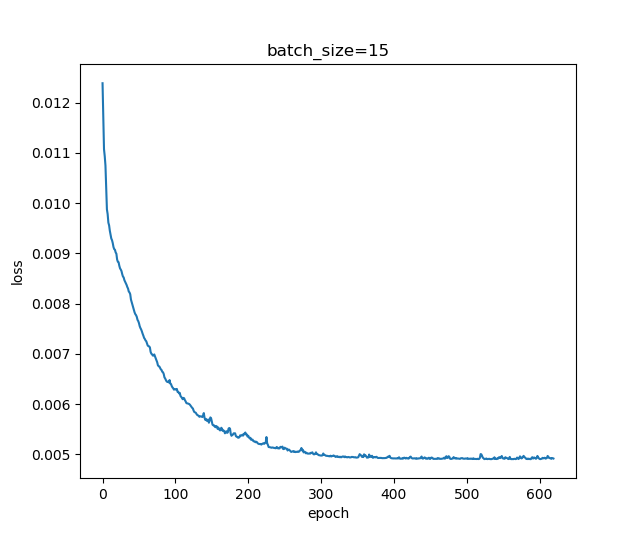
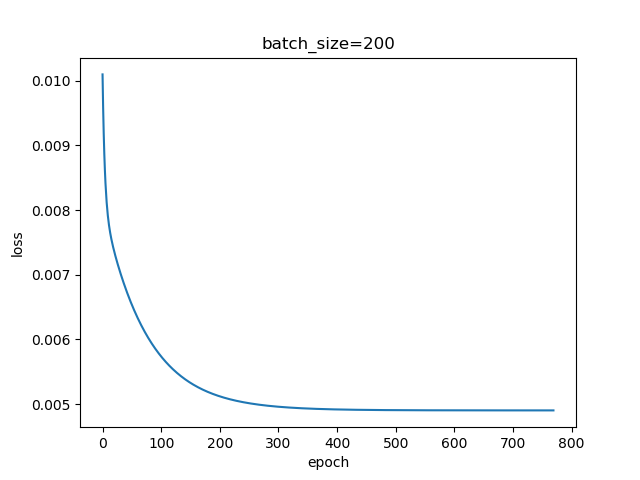
从以上结果可以看出随着批量的增加，迭代过程的波动逐渐变小，收敛速度变快。

四、问题解答

1. 为什么是椭圆而不是圆？如何把这个图变成一个圆？

   本质上讲这个是因为w,b对loss函数的影响程度不同造成的：

\[\begin{array}{l}{\text {Loss}=\frac{1}{m} \sum_{i=1}^{m}\left(w x_{i}+b-y_{i}\right)^{2}} \\ {\quad=\frac{1}{m} \sum_{i=1}^{m}\left(x_{i}^{2} w^{2}+b^{2}+2 x_{i} w b-2 y_{i} b-2 x_{i} y_{i} w\right)+c o n s t} \\ {\quad=\frac{1}{m} \sum_{i=1}^{m} x_{i}^{2} w^{2}+b^{2}+\frac{2}{m} \sum_{i=1}^{m} x_{i} w b-\frac{2}{m} \sum_{i=1}^{m} y_{i} b-\frac{2}{m} \sum_{i=1}^{m} x_{i} y_{i} w+c o n s t}\end{array} \]

由上的推导可知：loss的函数为双曲椭圆，若想让图像为圆，需要消去交叉项以及让w,b前面的系数相同。

2. 为什么中心是个椭圆区域而不是一个点？

   因为梯度下降方法受到步长的限制，在一个极小的区域内原本设定的学习率会使目标函数不断震荡。如下图：
   
   我们可以想象在一个学习率能到达的最小势阱中；迭代的情况不断在一个等势面上跳来跳去，永远也不能下降。最终所能到达的等势面的投影就是最小的椭圆。
   并且在loss2d函数中我们对loss函数值进行了四舍五入，这样造成的误差会让中心区域计算出的loss值趋于同一值。

五、解答验证

这是几张不同eta值；不同四舍五入状态下的loss2d图：




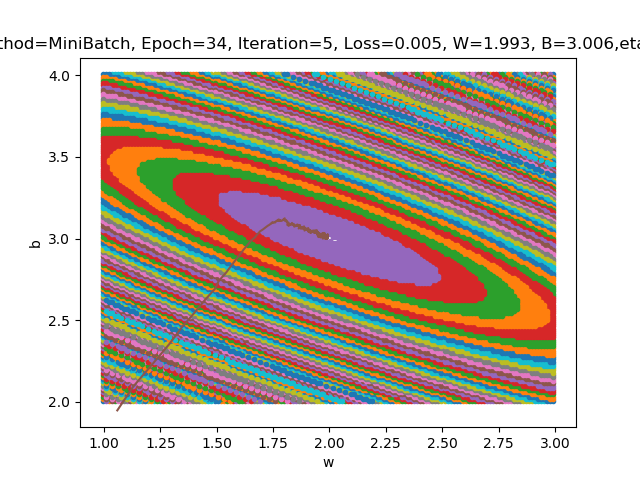
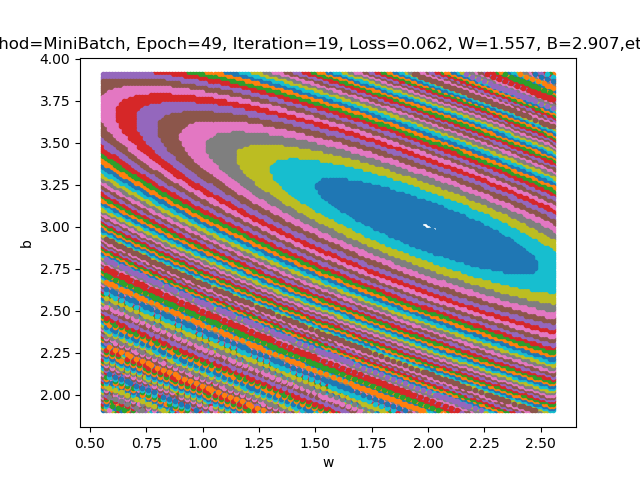
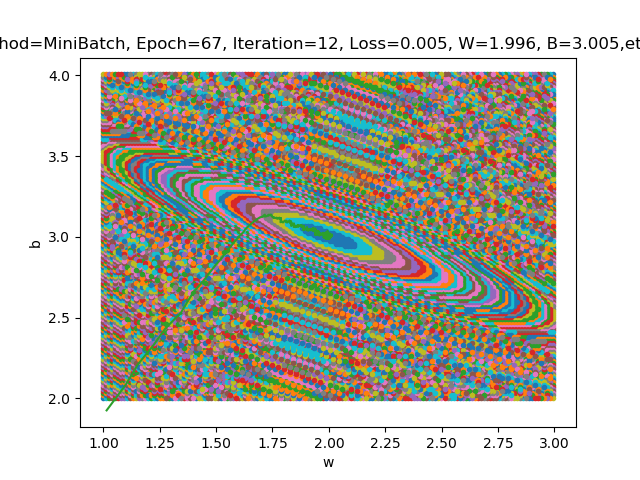
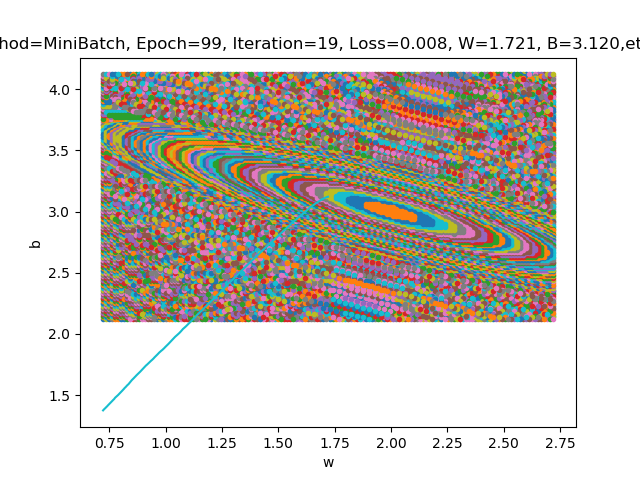
这四张图分别对应；eta=0.1;四舍五入2位；eta=0.002;四舍五入2位；eta=0.1;四舍五入3位；eta=0.002；四舍五入3位。可以看出四舍五入对最后椭圆大小的影响十分明显;eta的改变受四舍五入后数据影响；结果不明显。