[NOIP2007 普及组] Hanoi 双塔问题

题目链接：https://www.luogu.com.cn/problem/P1096

试题分析：

我们可以先根据一个盘子的汉诺塔问题来寻找规律：

一方面，对于n+1个盘，先用f(n)次移动将1至n号盘移到第三根柱子上，再将n+1号盘移到中间的柱子上，最后再用f(n)次将1至n号盘移到中间的柱子上，故2f(n)+1次能完成n+1个盘的移动，即f(n+1 ) ≤ 2f(n)+1 。

另一方面，考虑第n+1 号盘第一次被移动，此时1至n号盘必然均在另一根柱子上，因n个盘时最少移动次数为f(n)，故在n+1号盘第一次被移动之前，已经移动了至少f(n)次；类似的，考虑第n+1号盘最后一次被移动之后，1至n号盘亦均在另一根柱子上，故还需移动至少f(n)次，即f(n+1 ) ≥ f(n)+1+f(n)。

综上，f(n+1)=2f(n)+1，并且由上述证明不难看出：满足移动次数最少的移动方案是唯一的，即第三段中所述的移动方案。

另外，通过f（n+1）+1=2（f（n）+1）可得f(n)=2^n-1。

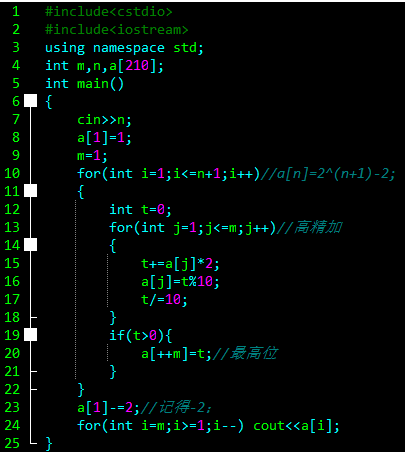
$由此，我们得出了一个盘子时的汉诺塔规律，两个盘子也就是在一个盘子的基础上*2，所以最终规律为f(n)=2^(n+1)-2。$

$注意：题目n的范围最大为200，所以我们这里需要用高精度。$

$代码：$