有点意思的题

个人认为有点意思的题，判定可能很迷。

ABC410G Longest Chord Chain

Tag: 断环为链 LIS

我们发现，这个圆十分不好搞，考虑断环为链。

断完之后，原图长的就是这样：

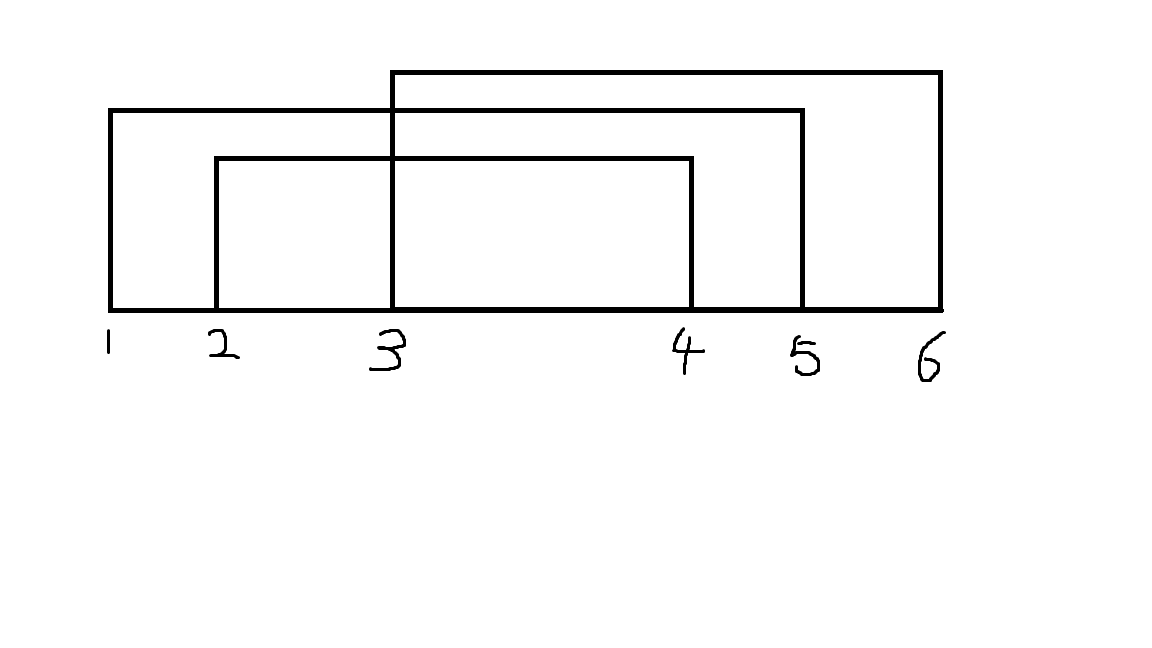
问题转化为选至多两个不交的部分，每个部分满足 \(l _ 1 \lt l _ 2 \lt \ldots \lt l _ k \wedge r _ 1 \gt r _ 2 \gt \ldots \gt r _ k\)，使得包含的线段尽量多。

升序排序 \(r\) 之后，一个部分就是 \(l\) 的最长下降子序列。

第一部分是没有限制的，设 \(dp _ i\) 表示以 \(i\) 结尾的最长下降子序列，则 \(dp _ i = 1 + \max \limits _ {j \lt i \wedge l _ j \gt l _ i}dp _ j\)。

第二部分的限制是与第一部分无交，钦定第二部分在第一部分后面，则我们直接更新 \(dp\) 数组，由于我们的 \(r\) 已经排好序了，所以 \(j \gt i\) 被天然满足，因此有 \(dp _ i = dp _ i + \max \limits _ {l _ j \gt r _ i} dp _ j\)。

那就好搞了，开棵线段树，维护 \(l _ i\) 对应的 \(dp\) 值，正常转移第一部分，然后复用线段树，直接查询 \([r,2n]\) 求出第二部分。

JOI2015A Copy and Paste 2

Tag：正难则反

显然这玩意不能直接维护，发现这个 \(k\) 很小，考虑一个 \(\Omicron(nk)\) 的算法。

最后的位置是固定的，所以我们可以对这个位置的所属区间分类讨论，设 \(len = b _ p - a _ p\)：

• \(i \le c _ p\)：这个操作没有影响到，不变。
• \(i \in [c _ p + 1,c _ p + len]\)：是复制的区间，转到原区间，\(i \gets i - c _ p + a _ p\)
• \(i \gt c _ p + len\)：是后面的区间，直接减去区间长度，\(i \gets i - len\)

然后没了，对每个位置直接模拟输出。