CS61A Fall 2020 Homework 2 Recursion 我的思路
HW2 Description: https://inst.eecs.berkeley.edu/~cs61a/fa20/hw/hw02/
我会把题目倒着放,因为通常后面的题能带给我的思考更多(也更可能做不出来😂)…… 放在后面我以后revisit的机会就更少了~
Q5: Anonymous factorial (并没有做出来)
The recursive factorial function can be written as a single expression by using a conditional expression.
>>> fact = lambda n: 1 if n == 1 else mul(n, fact(sub(n, 1)))>>> fact(5)120
Write an expression that computes n factorial using only call expressions, conditional expressions, and lambda expressions (no assignment or def statements). Note in particular that you are not allowed to use make_anonymous_factorial in your return expression. The sub and mul functions from the operator module are the only built-in functions required to solve this problem.
这道题实在是不会……先写了下有lambda但是也有recursion的情况:
def fact(n):
"""Sample
>>> fact(5)
120
"""
return 1 if n == 1 else mul(n, fact(sub(n, 1)))看看以后有没有机会想明白吧……
Q4: Count coins
Given a positive integer total, a set of coins makes change for total if the sum of the values of the coins is total. Here we will use standard US Coin values: 1, 5, 10, 25. For example, the following sets make change for 15:
- 15 1-cent coins
- 10 1-cent, 1 5-cent coins
- 5 1-cent, 2 5-cent coins
- 5 1-cent, 1 10-cent coins
- 3 5-cent coins
- 1 5-cent, 1 10-cent coin
Thus, there are 6 ways to make change for 15. Write a recursive function count_coins that takes a positive integer total and returns the number of ways to make change fortotalusing coins. Use the next_largest_coin function given to you to calculate the next largest coin denomination given your current coin. I.e. next_largest_coin(5) = 10.
Hint: Refer the implementation of count_partitions for an example of how to count the ways to sum up to a total with smaller parts. If you need to keep track of more than one value across recursive calls, consider writing a helper function.
想法:
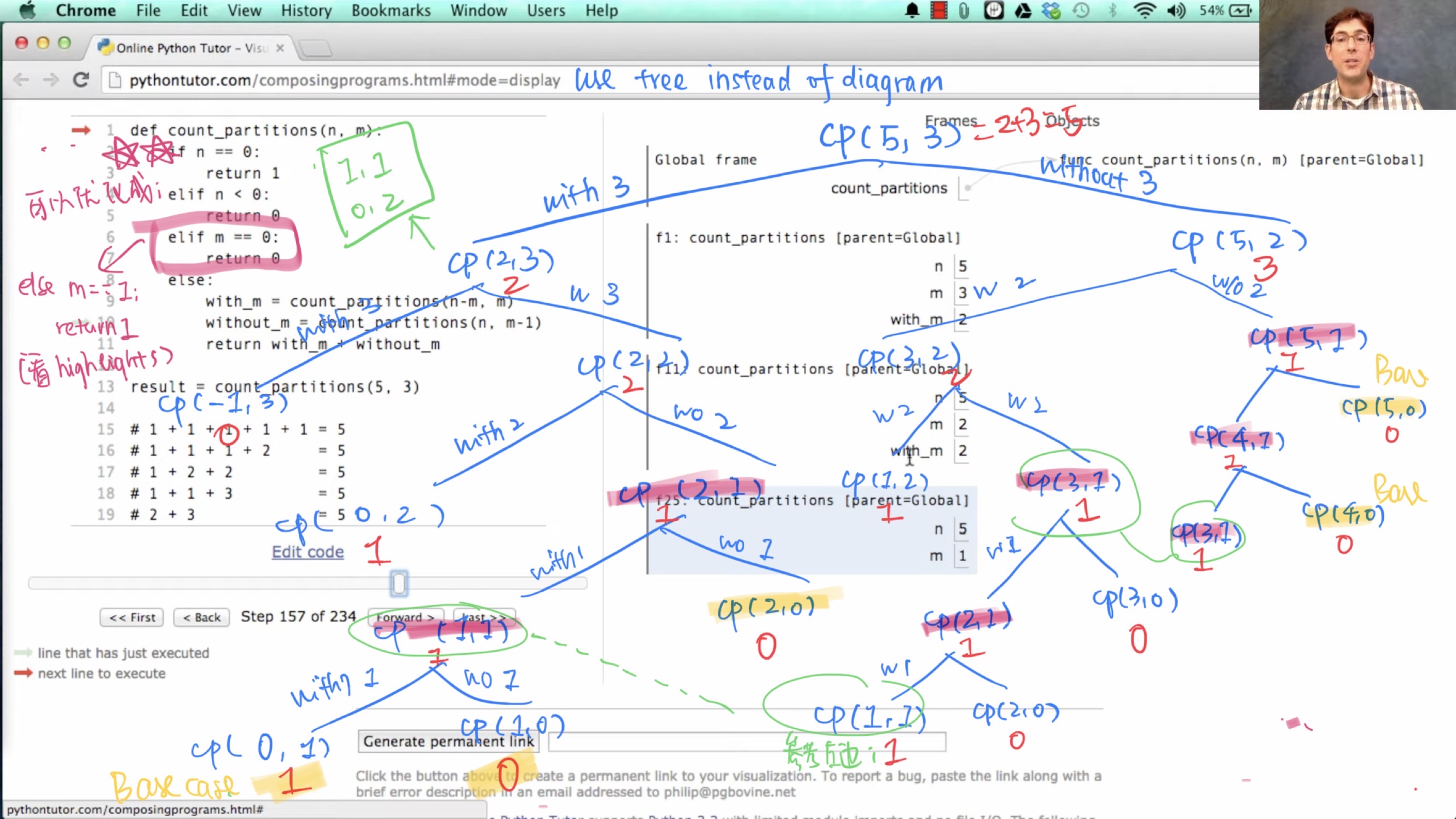
这道题也不允许用while或者loop的循环语句,要求用递归处理。count_partitions的implementation和tree_recursion大概看起来是下图这样子的,极简单但是跑起来费时间。
我的想法是:1)和higher-order-function不同,这种recursion,特别是double recursion的问题,用environment diagram非常不好懂,吃力不讨好,还不如直接画树来得快;
2)找对base case可以省很多步,比如下面的code,如果把elif m==0: return 0改成elif m == 1: return 1,那树下最后一步的分解都省了,input够大的时候大概能节省一半的步骤吧。
思路:
这道题需要一个helper2 func(2个input的function)来做。
我先用28的例子画了棵树(下图)(为什么是28呢,因为这涵盖了用上25的硬币的可能性)。
图示说明:例如helper2(28, 5)就是说找28分,其中有1个5美分、(注意隐藏statement)其他都用1美分补齐(这样就只有1种可能的组合)。
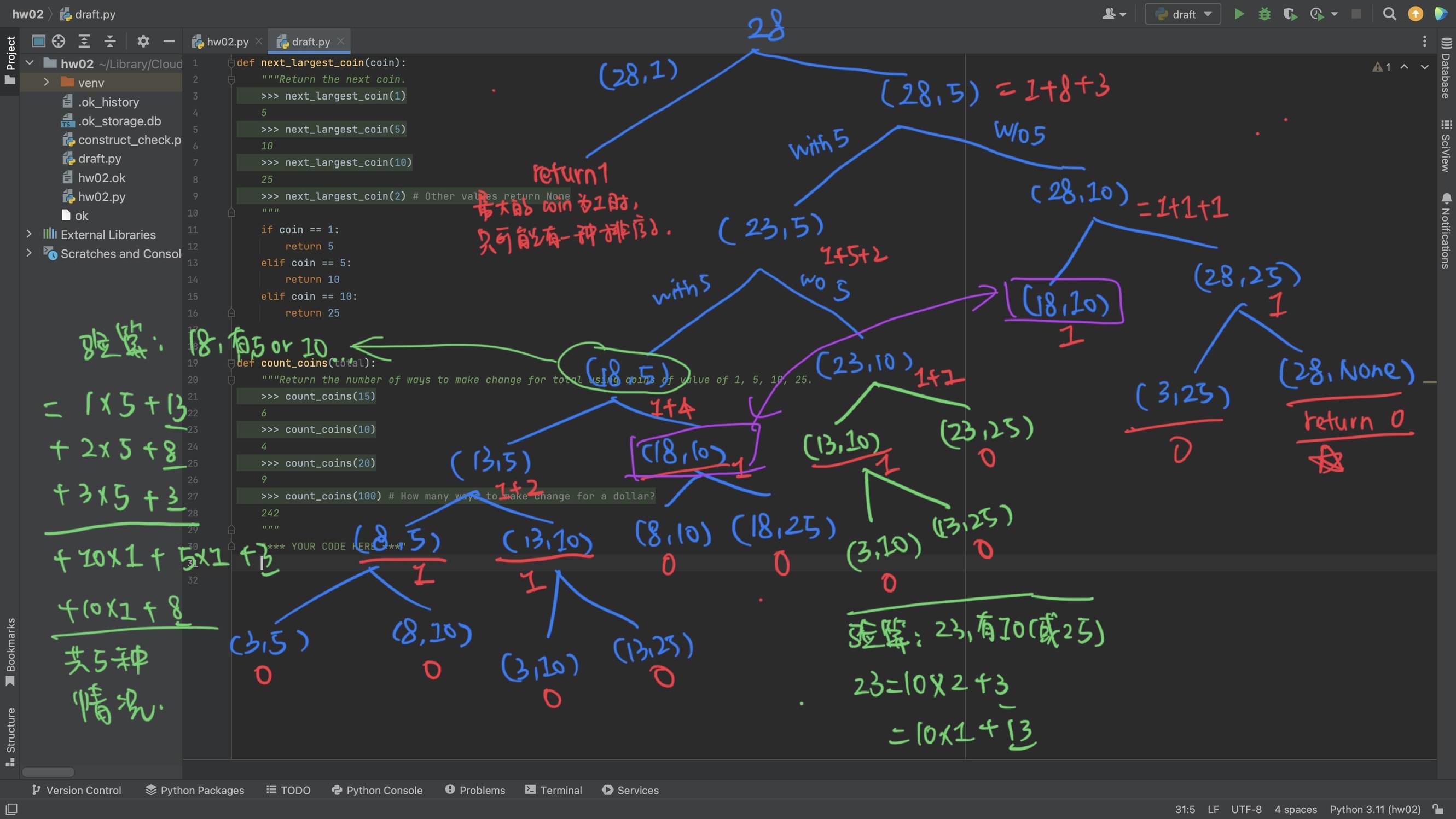
可以看到基本的递归就是helper2(n, coin) = 1 + helper2(n-coin, coin) + helper2(n, next_coin):
1是当前的function call:如果可以成功call成功,就代表存在这样1种combination,因此返回值里加上1helper2(n-coin, coin)是左边的分叉,helper2(n, next_coin)则是右边的分叉
在此之上有几种特殊情况需要处理:
- 如果n<coin,那么不存在这种组合,return0,上图中树底下的基本都是这种情况
- 如果最大的coin是1, 那么左边的分叉为0
- 如果最大的coin是25,右边的分叉为0
这个初代helper function大概看起来就是这样:
def count_with_xl_coin(tot, xl=1): # tot for total, xl stands for largest_coin
if tot < xl:
return 0
elif xl == 1:
with_next_xl_coin = count_with_xl_coin(tot, next_largest_coin(xl))
return 1 + 0 + with_next_xl_coin
elif xl == 25:
with_xl_coin = count_with_xl_coin(tot - xl, xl)
return 1 + with_xl_coin + 0
else:
with_xl_coin = count_with_xl_coin(tot - xl, xl)
with_next_xl_coin = count_with_xl_coin(tot, next_largest_coin(xl))
return 1 + with_xl_coin + with_next_xl_coin代码:
def next_largest_coin(coin):
"""Return the next coin.
>>> next_largest_coin(1)
5
>>> next_largest_coin(5)
10
>>> next_largest_coin(10)
25
>>> next_largest_coin(2) # Other values return None
"""
if coin == 1:
return 5
elif coin == 5:
return 10
elif coin == 10:
return 25
def count_coins(total):
"""Return the number of ways to make change for total using coins of value of 1, 5, 10, 25.
>>> count_coins(15)
6
>>> count_coins(10)
4
>>> count_coins(20)
9
>>> count_coins(28) # My own test case as illustrated in the chart
13
>>> count_coins(100) # How many ways to make change for a dollar?
242
"""
"*** YOUR CODE HERE ***"
def count_with_xl_coin(tot, xl=1): # tot for total, xl stands for largest_coin
if tot < xl:
return 0
else:
with_xl_coin = 0 if xl == 1 else count_with_xl_coin(tot - xl, xl)
with_next_xl_coin = 0 if xl == 25 else count_with_xl_coin(tot, next_largest_coin(xl))
return 1 + with_xl_coin + with_next_xl_coin
return count_with_xl_coin(total)Q3: Missing Digits
Write the recursive function missing_digits that takes a number n that is sorted in increasing order (for example, 12289 is valid but 15362 and 98764 are not). It returns the number of missing digits in n. A missing digit is a number between the first and last digit of n of a that is not in n. Use recursion - the tests will fail if you use while or for loops.
思路:
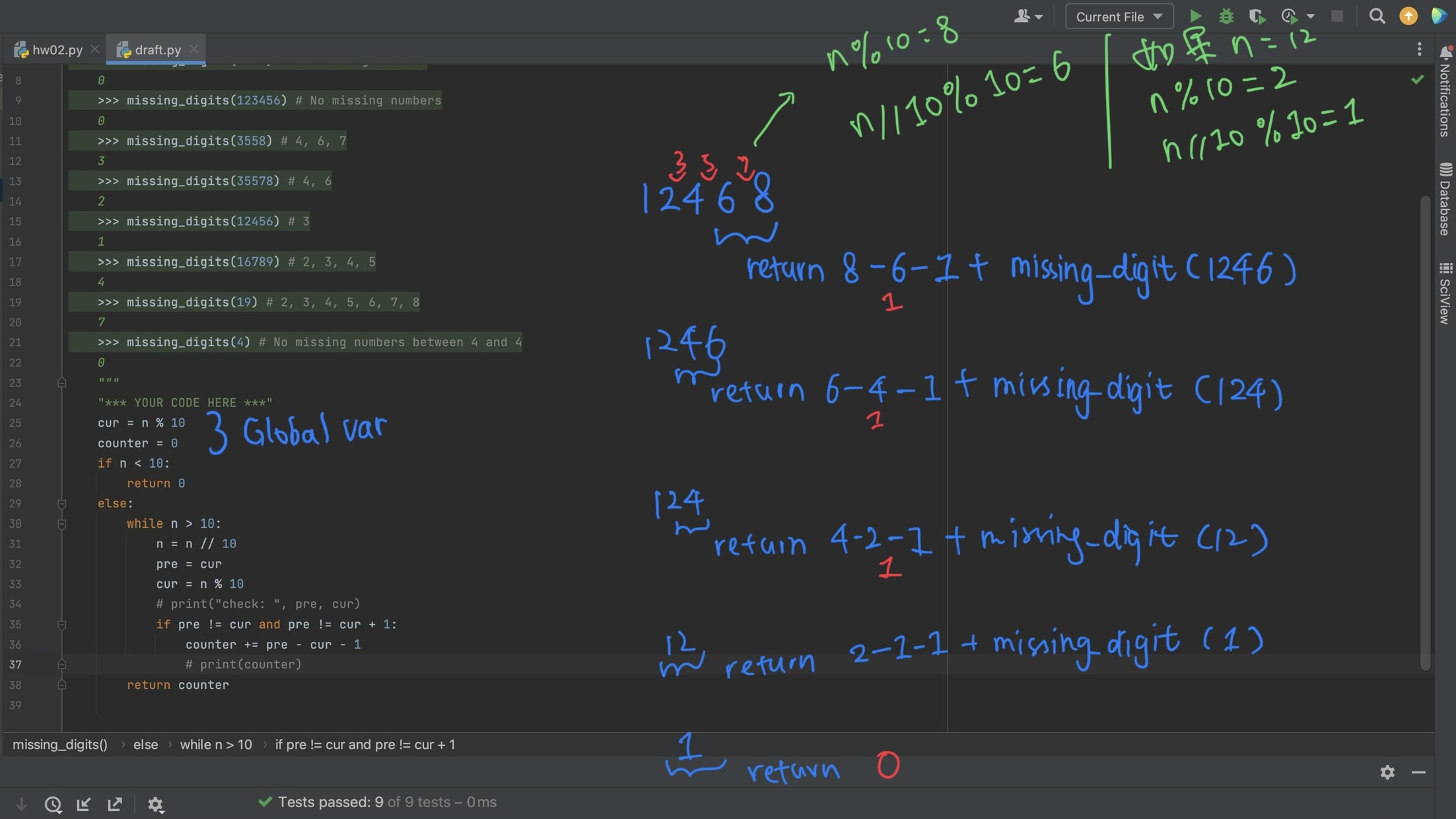
做完前两题其实就觉得第三题比较简单了,思路都是类似的,我用下面一个例子(12468)来找规律(其实我还先写了个循环解法,帮助总结思路用的):
首先,不考虑算法好坏时,递归可以是12468-1246-124-12-1(每次只前进一个digit),这个会构成返回值的其中一部分。
注意,每次要检查的两位数,最后一个数可以用n%10表示,倒数第二位数可以用n//10%10表示,但要注意,这里潜在的要求是n有两位数以上,所以base case就变成n<10了。
其次,再细看每次检查的两位数,比如66(间隔为0)或者67(间隔为0)或者68(间隔为1 = 8-6-1)或者69(间隔为2 = 9-6-1),这个会构成返回值的另一部分,这部分将由if控制。
代码:
def missing_digits(n):
"""Given a number a that is in sorted, increasing order,
return the number of missing digits in n. A missing digit is
a number between the first and last digit of a that is not in n.
>>> missing_digits(1248) # 3, 5, 6, 7
4
>>> missing_digits(1122) # No missing numbers
0
>>> missing_digits(123456) # No missing numbers
0
>>> missing_digits(3558) # 4, 6, 7
3
>>> missing_digits(35578) # 4, 6
2
>>> missing_digits(12456) # 3
1
>>> missing_digits(16789) # 2, 3, 4, 5
4
>>> missing_digits(19) # 2, 3, 4, 5, 6, 7, 8
7
>>> missing_digits(4) # No missing numbers between 4 and 4
0
"""
"*** YOUR CODE HERE ***"
if n < 10:
return 0
else:
cur, nxt = n % 10, n // 10 % 10
if cur == nxt:
return 0 + missing_digits(n // 10) # can omit 0, put it here just for clarity
else:
return cur - nxt - 1 + missing_digits(n // 10)Q2: Ping-pong
The ping-pong sequence counts up starting from 1 and is always either counting up or counting down. At element k, the direction switches if k is a multiple of 8 or contains the digit 8. The first 30 elements of the ping-pong sequence are listed below, with direction swaps marked using brackets at the 8th, 16th, 18th, 24th, and 28th elements:
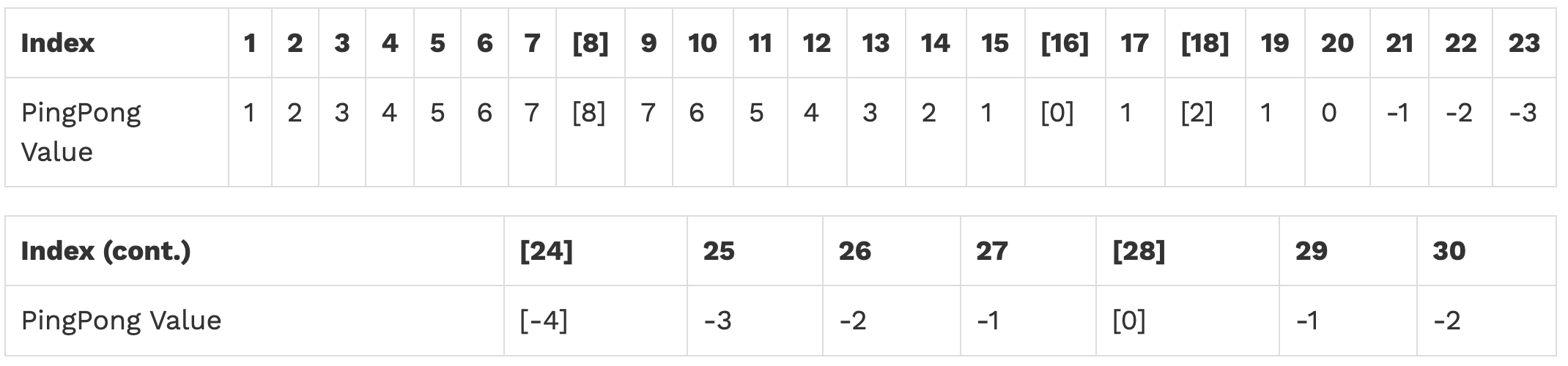
Implement a function pingpong that returns the nth element of the ping-pong sequence without using any assignment statements.
You may use the function num_eights, which you defined in the previous question.
Use recursion - the tests will fail if you use any assignment statements.
思路:
pp(9) = pp(8) - 1
pp(8) = pp(7) + 1
pp(7) = pp(6) + 1
...
pp(2) = pp(1) + 1
pp(1) = 0 + 1 --> Base case is pp(1)
Other than base case, pp(n) = pp(n-1) + direction(n-1)
---------------------------------
这里需要注意,direction是一个accumulated的值,所以没办法直接返回一个常数,需要借助一个helper function实现。
换句话说,要知道direction(n),需要知道direction(n-1)是什么,以及index(n-1)的位置上有没有发生方向的反转。
沿用上面的例子
d(9) 返回 -d(8),因为8满足了某些条件(x%8==0,或者x有8-->注意,检查有没有8可以套用第一题num_eights来做)
d(8) 返回 d(7)
d(7) 返回 d(6)
...
d(2) 返回 d(1)
pp(1) 返回 1 --> Base case is pp(1), return 1
代码:
def pingpong(n):
"""Return the nth element of the ping-pong sequence.
>>> pingpong(8)
8
>>> pingpong(10)
6
>>> pingpong(15)
1
>>> pingpong(21)
-1
>>> pingpong(22)
-2
>>> pingpong(30)
-2
>>> pingpong(68)
0
>>> pingpong(69)
-1
>>> pingpong(80)
0
>>> pingpong(81)
1
>>> pingpong(82)
0
>>> pingpong(100)
-6
"""
"*** YOUR CODE HERE ***"
# Helper func: Check the direction value at index position x
# Since the value ia accumulated, we need to track it in a separate function
def direction(x):
if x == 1:
return 1
elif num_eights(x) != 0 or x % 8 == 0:
return -direction(x - 1)
else:
return direction(x - 1)
# Base case: pingpong(1) is 0(default acc value) + 1(direction)
# Else: pingpong(n) = pingpong(n-1) + direction(n-1)
if n == 1:
return 0 + direction(1) # we put 0 here merely for clarity; can drop it if needed
else:
return pingpong(n - 1) + direction(n - 1)其他:
如果不想套用num_eights,一个思路是在ping_pong里再加一个helper functioncheck(x),如果返回值为真,则x含有至少一个8
相应的elif num_eights(x) != 0 or x % 8 == 0应该修改成elif check(x) or x % 8 == 0
# Helper func: Check whether index x contains '8'
def check(x):
if x < 10:
return x == 8
elif x % 10 == 8:
return True
else:
return check(x // 10)Q1: Num eights
Write a recursive function num_eights that takes a positive integer x and returns the number of times the digit 8 appears in x. Use recursion - the tests will fail if you use any assignment statements.
思路:
ne(2863) = 0 + ne(286)
ne(286) = 0 + ne(28)
ne(28) = 1 + ne(2)
ne(2) = 0 + ne(0)
由上述例子可看到,每次recursion只检查last digit就可以,这可以用x // 10实现
具体递归实现,用num_eights(x)返回0/1 + num_eights(x-1)实现,直到base casenum_eights(0)
代码:
def num_eights(x):
"""Returns the number of times 8 appears as a digit of x.
>>> num_eights(3)
0
>>> num_eights(8)
1
>>> num_eights(88888888)
8
>>> num_eights(2638)
1
>>> num_eights(86380)
2
>>> num_eights(12345)
0
"""
"*** YOUR CODE HERE ***"
if x == 0:
return 0
elif x % 10 == 8:
return 1 + num_eights(x // 10)
else:
return num_eights(x // 10)
 浙公网安备 33010602011771号
浙公网安备 33010602011771号