P4838 题解

P4838 P哥破解密码题解

• 原题面

思路貌似跟dalao们的有点不一样

先前排声明一下,蒟蒻刚学OI没多久,而且是自学的,写的可能比较累赘，望见谅

• 大致题意

---

给一串长度为n的字符串,当且仅当串只由A和B构成，且没有连续的3个A时,该串合法,求方案总数

---

感觉跟P4910帕秋莉的手环那道题目差不多吧....都是线性递推,貌似dalao们都是用动态规划来做的,蒟蒻不太会,所以只好用比较sb的递推来做qwq

• 思路

既然每个字符只有A和B两种可能,,如果字符串没有任何限制的话,很容易看出方 案总数为 : \(2^n\)

但这里加了一个不能有没有连续的3个A出现的限制条件

不妨先来画个图来看一下,更加直观一点

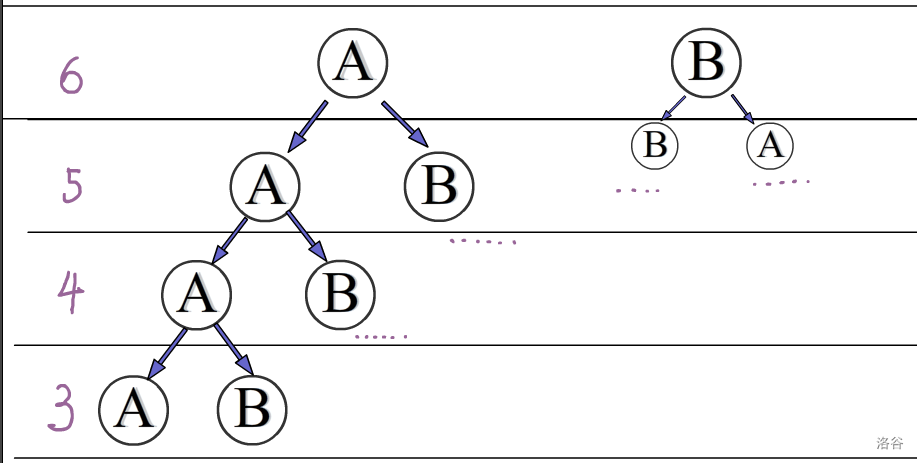
图中为n=6的时候的情况

我们用\(f_i\)来表示长度为i的字符串的不合法方案总数(注意,是不合法方案总数)

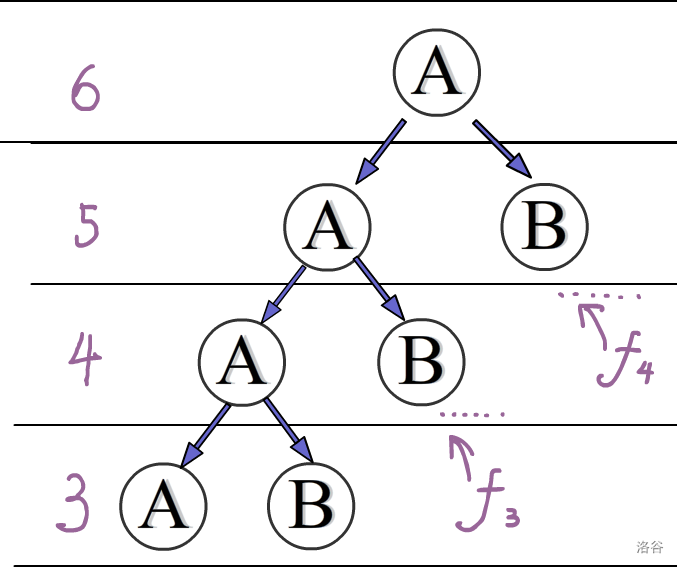
先来看第一个字符选A情况

这里我们可以把每一个B看作是一个"断点"

不难看出,每出现一个断点后

该断点下面的情况就可以从之前的\(f_i\)递推过来

而当出现连续3个A时,相当于是把下面的所有情况都"截断"了

也就是\(2^{n-3}\)种情况

第一个字符选"B"也同理

相当于是在第一个点的时候就把该串给"截断"了

容易推出当N=6时,合法方案总数为

\(2^6-(f_{5}+f_{4}+f_{3}+2^3)\)

其他n>3的情况也同理

得到式子

方案总数=\(2^n-(f_{n-1}+f_{n-2}+f_{n-3}+2^{n-3})\)

=\(7*2^{n-3}-(f_{n-1}+f_{n-2}+f_{n-3})\)

=\((2^{n-1}+2^{n-2}+2^{n-3})-(f_{n-1}+f_{n-2}+f_{n-3})\)

设\(s_i\)为方案总数

则\(s_i=s_{i-1}+s_{i-2}+s_{i-3}\)

得到最终式子
\(\begin{cases}2(n=1)\\4 (n=2)\\7 (n=3)\\s_i=s_{i-1}+s_{i-2}+s_{i-3}(n>3)\end{cases}\)

贴个丑陋的代码

#include<bits/stdc++.h>
using namespace std;
int mo=19260817;
long long n,t;
struct matrix{
	long long int a[5][5];
}ans,a;
matrix operator *(const matrix &x,const matrix &y){
	matrix z;
	for(int i=1;i<=3;i++){
		for(int j=1;j<=3;j++){
			z.a[i][j]=0;
		}
	}
	for(int k=1;k<=3;k++){
		for(int i=1;i<=3;i++){
			for(int j=1;j<=3;j++){
				z.a[i][j]=(z.a[i][j]+(x.a[i][k]*y.a[k][j])%mo)%mo;
			}
		}
	}
	return z;
}
int main(){
	cin>>t;
	while(t--){
		cin>>n;
		if(n==1){
			cout<<2<<endl;
		}
		
	else if(n==2){
		cout<<4<<endl;
	}
	else if(n==3){
		cout<<7<<endl;
	} 
	else{
		for(int i=1;i<=3;i++){
				for(int j=1;j<=3;j++){
					a.a[i][j]=0;
					if(i==j) ans.a[i][j]=1;
					else ans.a[i][j]=0;
				}
			}
		a.a[1][1]=a.a[1][2]=a.a[1][3]=a.a[2][1]=a.a[3][2]=1; 
		
		
		while(n){
			if(n&1) ans=ans*a;
			n>>=1;
			a=a*a;
		}
		cout<<((ans.a[1][1]+ans.a[2][1])%mo+ans.a[3][1])%mo<<endl;
	}
	
	}
	return 0;
}

貌似是蒟蒻的第一次不看题解做出(比较水的)紫题?