注意力机制
传统的编码-解码机制
attention和self-attention 的区别
- 具体计算过程是一样的
- 计算对象不同,attention是source对target的attention,而self attention 是source 对source的attention。
- attention用于Seq2Seq; self-attention可单个的网络,是RNN和CNN的特殊情况!
- attention告诉的是每个部分的重要程度,self-attention告诉的是各个部分的关联关系
设输入序列{x1,x2,...,xn},输出序列{y1,y2,...,ym},encoder的隐向量为h1,h2,...,decoder的隐向量为s1,s2,...。
解码器的输入只有一个向量,该向量就是输入序列经过编码器的上下文向量c 。
这种固定长度的上下文向量设计的一个关键而明显的缺点是无法记住长句子。通常,一旦完成了对整个输入的处理,便会忘记第一部分。注意力机制诞生了(Bahdanau et al,2015)来解决这个问题。


Attention 编码-解码机制
- Attention的定义
attention是一种提升encoder-decoder模型效果的机制,一般称作attention mechanism。
![]()
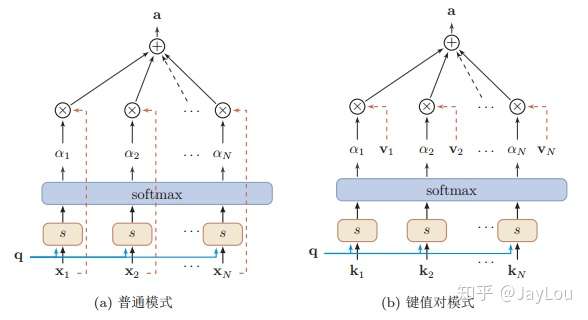
(1) 普通模式
注意力机制可以分为三步:一是信息输入;二是计算注意力分布α;三是根据注意力分布α 来计算输入信息的加权平均。
step1-信息输入:用X = [x1, · · · , xN ]表示N 个输入信息;
step2-注意力分布计算:令Key=Value=X,则可以给出注意力分布
\(
α_i = softmax(s(key_i,q)) = softmax(s(X_i,q))
\)
注意力分布:为了从N个输入向量[x1,⋅⋅⋅,xN]中选择出和某个特定任务相关的 信息,我们需要引入一个和任务相关的表示,称为查询向量(Query Vector),并通过一个打分函数来计算每个输入向量和查询向量之间的相关性。
给定一个和任务相关的查询向量q,我们用注意力变量z∈[1,N]来表示被选择信息的索引位置,即z=i表示选择了第i个输入向量。为了方便计算,我们采用一种“软性”的信息选择机制。首先计算在给定q和X下,选择第i个输入向量的概率\(a_i\)
其中 \(α_i\) 称为注意力分布(Attention Distribution),\(s(x_i,q)\) 为注意力打分函数, 可以使用以下几种方式来计算:
其中\(W、U、v\)为可学习的参数,d为输入向量的维度。
理论上,加性模型和点积模型的复杂度差不多,但是点积模型在实现上可以更好地利用矩阵乘积,从而计算 效率更高。但当输入向量的维度 d 比较高,点积模型的值通常有比较大方差,从 而导致softmax函数的梯度会比较小。因此, 缩放点积模型可以较好地解决这个问题。
双线性模型可以看做是一种泛化的点积模型。假设双线性模型公式中$W=U^TV$ ,双线性模型可以写为 \(s(x_i,q)=x^T_iU^TVq=(Ux)^T(Vq)\),即分别对x和q进行 线性变换后计算点积。相比点积模型,双线性模型在计算相似度时引入了非对称性。
加权平均:注意力分布αi可以解释为在给定任务相关的查询q时,第i个输入向量受关注的程度。我们采用一种“软性”的信息选择机制对输入信息进行汇总
\(
att(q,X) = \sum_{i=1}^Nα_iX_i
\)
这种编码方式为软性注意力机制(soft Attention),软性注意力机制有两种:普通模式(Key=Value=X)和键值对模式(Key!=Value)。
更一般地,我们可以用键值对(key-value pair)格式来表示输入信息,其中 “键”用来计算注意力分布\(α_i\),“值”用来计算聚合信息。
键值对注意力机制
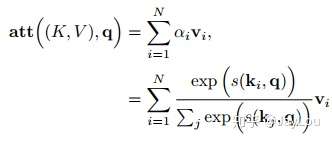




 浙公网安备 33010602011771号
浙公网安备 33010602011771号