QOJ10272 题解

图连通性问题。难点在于建立尽量少的边使得连通性不变。

题意：给定长度为 \(n\) 的序列 \(a\)。\(l,r\) 之间连边当且仅当 \(a_{[l,r]}\) 中存在绝对众数。求总连通块个数。

Tips：一个长度为 \(n\) 的区间存在绝对众数当且仅当去年内存在数 \(x\) 的出现次数严格 \(>\frac{n}{2}\)。

套路化的枚举绝对众数 \(x\) 并把序列中是 \(x\) 的数变为 \(1\)，不是 \(x\) 的数变为 \(-1\)，然后作前缀和。那么 \((i,j)\) 有边当且仅当 \(s_j-s_{i-1}>0\)，那么 \(s_j\ge s_i\)。

还是要考虑如何去除一些冗余的边。显然当 \(a_i=a_j=-1\) 时边 \((i,j)\) 是冗余的。因为在 \([i,j]\) 中必然存在第一个 \(a_s=1\) 和最后一个 \(a_t=1\) 使得 \((i,t),(s,j),(s,t)\) 均有边。这样 \((i,j)\) 就无需连边了。

那么此时只剩下三种情况：

• \(a_i=a_j=1\)：由于 01 序列前缀和的性质，对于 \(s_i+1\le s_j-1\)，一定存在 \(i<k<j\) 使得 \((i,k),(k,j)\) 均有连边。那么 \((i,j)\) 这条边就是冗余的。于是我们只需要维护 \(s_i+1=s_j\) 和 \(s_i=s_j\) 的极小区间连边即可。开个桶就可以了。
• \(a_i=1,a_j=0\)：如图所示，
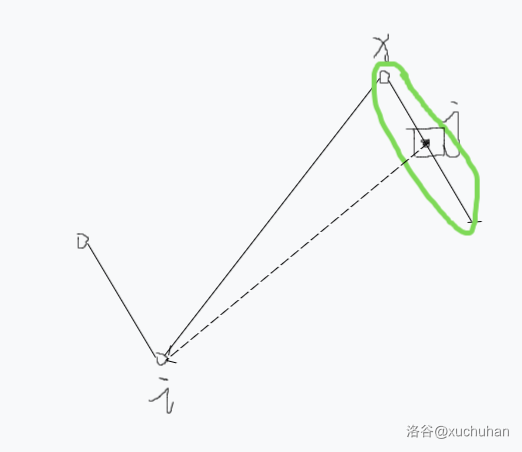
  我们画出前缀和的折线图。\(j\) 所在的那一段折线上，所有高度比「谷底」 \(i\) 高的都可以和 \(i\) 连边。也就是绿色框住的区间。此时 \(x\) 已经和 \(i\) 连过边（上一种情况），那么我们只需要将绿色区间的 \(0\) 两两首尾相接 \((i,i+1)\) 即可形成和统一连「谷底」同样的效果。那么我们用差分将绿色区间打个标记，最后再一起连 \((i,i+1)\)。
• \(a_i=0,a_j=1\)。和第二种情况同理，倒着处理并连「山顶」。

具体实现的时候由于无关 \(0\) 只在乎 \(1\)（\(0\) 差分后统一处理），所以对于每个众数 \(x\) 将 \(a_i=x\) 的位置 \(i\) 抠出来处理即可。那么这一块的复杂度就是线性的了。

代码：

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=2e6+5,inf=0x3f3f3f3f3f3f3f3f;
int T,n,ans,a[N],lst[N<<1],fa[N],diff[N];
vector<int>v[N];
int fd(int x){return (x==fa[x]?x:fa[x]=fd(fa[x]));}
void uni(int x,int y){x=fd(x),y=fd(y);if(x!=y)fa[x]=y;}
signed main(){
	cin>>T;
	while(T--){
		cin>>n;
		for(int i=1;i<=n;i++)lst[i]=lst[i+n]=-1,diff[i]=0,v[i].clear();
		for(int i=1;i<=n;i++)cin>>a[i],v[a[i]].push_back(i),fa[i]=i;
		for(int i=1;i<=n;i++){
			if(v[i].empty())continue;
			int now=inf;
			for(int j=0;j<v[i].size();j++){
				int s=(j+1<<1)-v[i][j]+n,x=v[i][j];
				if(lst[s]!=-1)uni(x,lst[s]);
				if(lst[s-1]!=-1)uni(x,lst[s-1]);
				if(now<s)diff[x]++,diff[min(n,x+s-now)]--;
				lst[s]=x,now=min(now,s);
			}
			now=-inf;
			for(int j=v[i].size()-1;j>=0;j--){
				int s=(j+1<<1)-v[i][j]+n,x=v[i][j];
				if(now>s)diff[x]--,diff[max(1ll,x+s-now)]++;
				lst[s]=-1,now=max(now,s);
			}
		}
		for(int i=1;i<n;i++){
			diff[i]+=diff[i-1];
			if(diff[i])uni(i,i+1);
		}
		for(int i=1;i<=n;i++)if(fd(i)==i)ans++;
		cout<<ans<<"\n",ans=0;
	}
	return 0;
}