金融学概论

资产类别（Asset Classes）

金融资产类别

固定收益类资产（Fixed-income/ Debt Securities）
- 货币市场工具（Money Market）
  - 国库债（Treasury Bills/ 短期国库券）
  - 存款证（Certificate of Deposit/ 存款凭证）
  - 商业票据（Commercial Paper/ 商业短期借据）
- 固定收益资本市场工具（Fixed-Income Capital Market）
  - 国库票据（Treasury Notes/ 中期政府债券）
  - 国债（Treasury Bonds/ 长期政府债券）
权益类证券（Equity Securities / 股票）
衍生品
- 期权（Options）
- 期货（Futures）
- 结构化金融产品（Structured Finance）
  - 债务担保证券（Collateralized Debt Obligation/ CDO）
  - 资产抵押债券（Asset-Backed Security/ ABS）

保证金购买（Buying on Margin）

维护保证金比例 = 净值 / 股票市值（做多做空都是这样）

如果低于一个比例需要追缴保证金。

基金（Funds）

小投资者的问题：

不能够构建足够多样化的投资组合
更高的交易成本
没有时间调研

因此需要基金。

基金类型

开放型（Open-end funds）基金（e.g. mutual funds, hedge funds）：由基金本身进行创建和赎回，投资者从基金本身购买份额，并在每个交易日结束时“净资产价值（NAV）”将份额卖回给基金。

封闭型（Closed-end funds）基金：在证券交易所上市交易，具有固定数量的已发行份额（可以通过额外发行补充），封闭型基金在投资者之间交易，交易价格通常不等于基金的净资产价值。

交易开放型指数（Exchanged-traded funds）基金（ETFs）是最新的一种基金类型，结合了开放式和封闭式基金的优点，ETF 的份额在交易所投资者之间交易，但设有一种套利机制，以使市场价格始终接近基金的净资产价值。

风险投资组合的历史收益

\[(1+\pi)(1+r)=1+i\\ r=\frac{1+i}{1+\pi}\approx i-\pi \]

名义回报率（nominal return）$i$
实际回报率（real return）$r$
通胀率（inflation rate）$\pi$

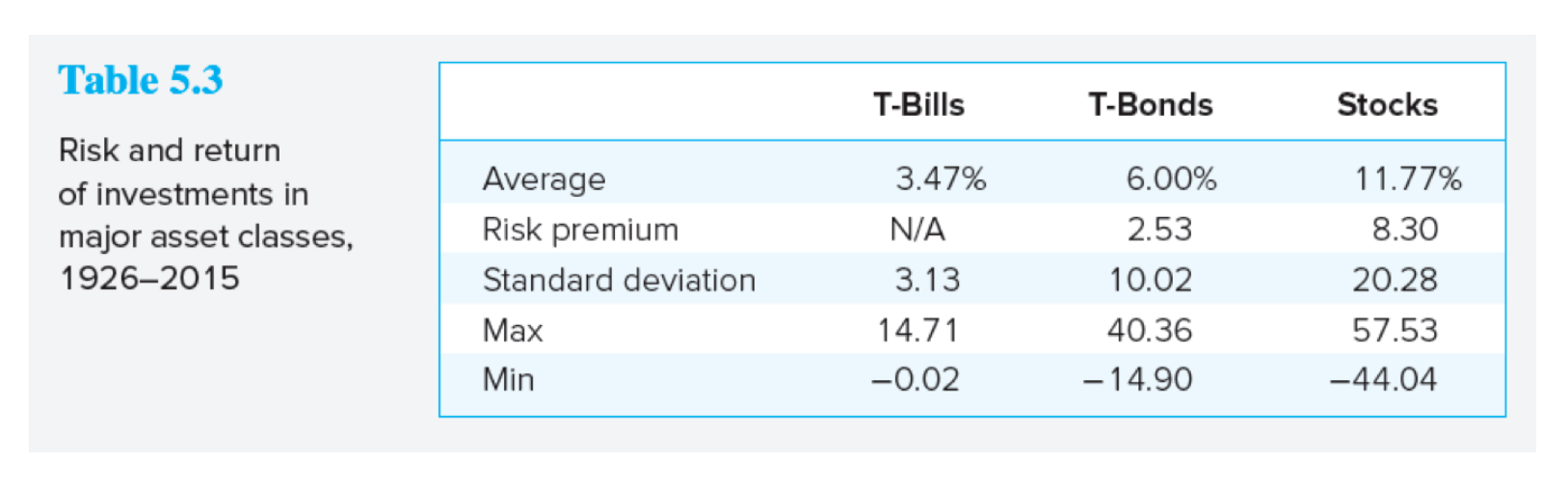
风险溢价（risk premium）是指风险资产的预期收益率-无风险利率（risk-free rate，如 T-bills）。

标准差用来衡量波动性、风险。

超额收益（excess return）：实际收益率-无风险收益率

投资组合介绍

效用函数：$U(X)$ 表示对这个资产的优先级，越大越优先。

假设投资者偏好只取决于资产的期望收益率和标准差，设效用函数形如：

\[U=E(r)-\frac{1}{2}A\sigma^2 \]

$E(r)$：期望收益率
$\sigma^2$：收益率的方差
$A$：投资者的风险厌恶系数。

根据这个可以在 $E(r)-\sigma$ 坐标轴上画出一个无差异曲线，在这条曲线上的效用函数相等。

构造投资组合（Constructing Portfolios）

假设只有两种资产 $1$ 和 $2$：

收益率是随机变量 $r_1,r_2$
期望收益率是 $E(r_1),E(r_2)$
标准差是 $\sigma_1,\sigma_2$
协方差是 $\sigma_{12}$
策略权重 $w_1,w_2$

设 $r_p$ 是投资组合的收益率（也是随机变量），那么什么决定了 $E(r_p)$ 和 $\sigma_{p}$？

\[E(r_p)=w_1E(r_1)+w_2E(r_2)\\ \sigma_p^2=w_1^2\sigma_1^2+w_2^2\sigma_2^2+2w_1w_2\sigma_{12} \]

无风险资产的组合策略（Portfolios with a risk-free asset）

设资产 $1$ 是无风险资产：$E(r_1)=r_f$ 且 $\sigma_1^2=0$。

那么 $\sigma_{12}=0$。

那么 $\sigma_p=w_2\sigma_2$。

设只有两种资产，无风险资产，收益率 $r_f$ 和风险策略 $P$，收益率 $r_p$，期望收益率 $E(r_p)$，标准差 $\sigma_p$。

这两种资产组合成一个组合策略 $C$，满足权重 $w_1+w_2=1$，设 $w_1=y$，那么 $w_2=1-y$。

\[\begin{aligned} E(r_c)&=(1-y)r_f+yE(r_p)\\ &=r_f+y(E(r_p)-r_f) \end{aligned} \]

其中 $E(r_p)-r_f$ 之前提过，叫做风险溢价（risk-premium）。

\[\sigma_c=y\sigma_p \]

定义夏普率/收益波动性比率（Reward-to-Volatility(Sharp) Ratio）$S$ 为：

\[S=\frac{\text{Risk premium}}{\text{SD of excess return}}=\frac{E(r_p)-r_f}{\sigma_p} \]

然后发现：

\[E(r_c)=r_f+y(E(r_p)-r_f)\\ E(r_c)=r_f+y\sigma_p S \]

由于 $\sigma_c=y\sigma_p$，于是

\[E(r_c)=r_f+S\sigma_c \]

所以 $E(r_c)$ 和 $\sigma_c$ 是线性关系，这条直线被称为资本配置线（Capital Allocation Line/CAL）

然后效用函数又是个二次函数，所以可以找到最优的点，效用函数最大。

\[\frac{\mathrm dU}{\mathrm dy}=0\\ y^*=\frac{E(r_p)-r_f}{A\sigma_p^2} \]

最优风险投资组合

市场风险/系统性风险/不可分散风险（Market risk）
公司特有风险/非系统性风险/可分散风险（Firm-specific risk）

两个风险资产的组合的方差会和协方差有关，可以设两个资产的权重解出最小方差组合。

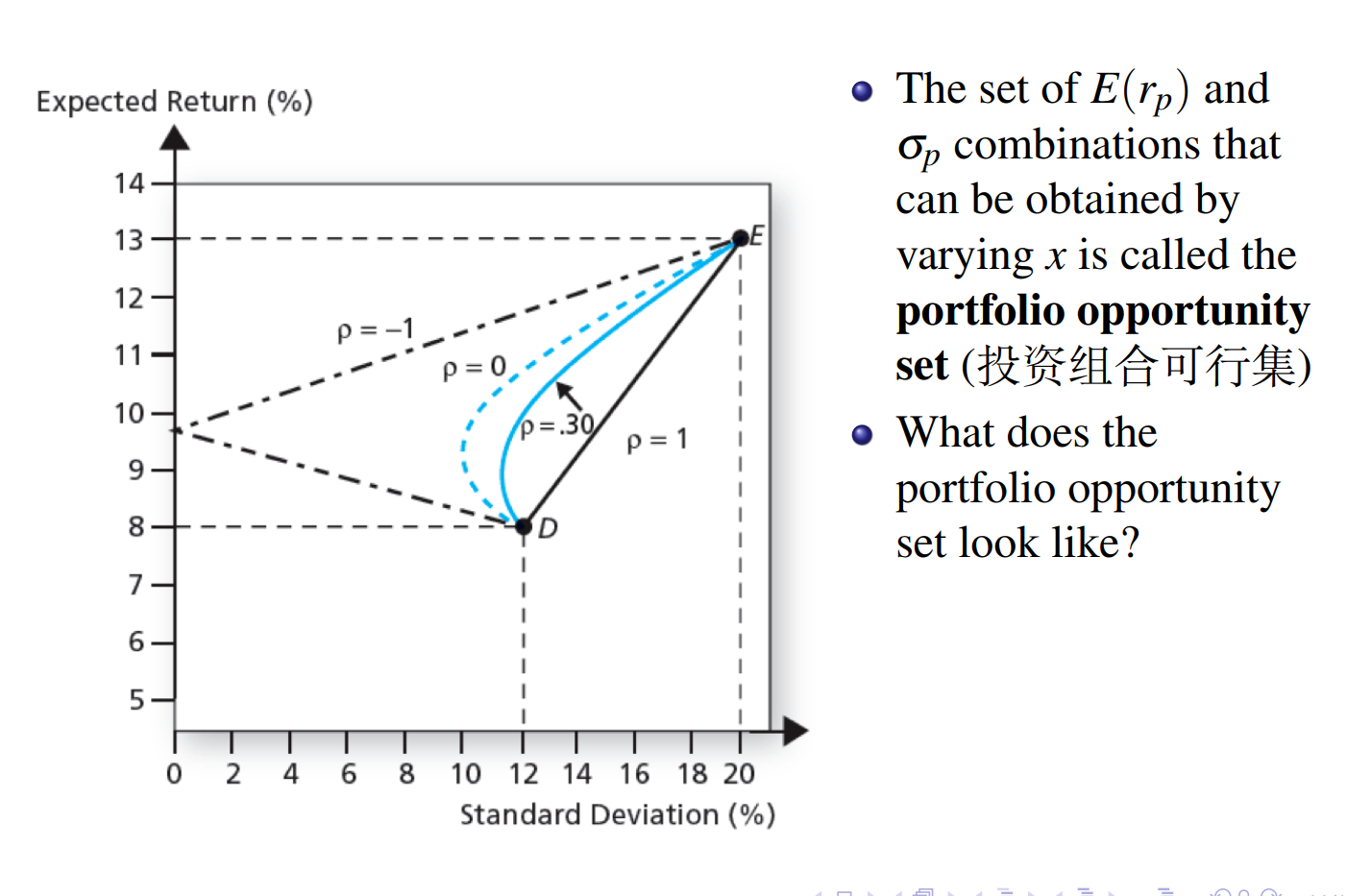
只有两个风险资产可以选择时，投资者只会选择上半段（因为下半段方差相同期望低）

多个风险资产组合也类似，会有一条最优的 CAL 连接无风险资产和切点，最优策略只可能选这条直线上（结论：所有投资者持有相同的风险投资组合）。

指数模型（Index Model）

\[R_i=r_i-r_f\\ R_i=\alpha_i+\beta R_m+e_i \]

$e_i$ 是随机变量反映了公司固有的风险
$\beta_i$ 反映了对影响所有证券的因子的敏感性（大、小、负都可能）

其中 $E(e_i)=0$（因为有 $\alpha_i$），$\mathrm{cov}(e_i,R_m)=0,\mathrm{e_i,e_j}=0$，$e_i$ 的方差为 $\sigma^2(e_i)$。

给定 $T$ 个点值 $(R_i,R_m)$，可以算 $e_i=R_i-(\alpha_i+\beta_iR_m)$，用 $\frac 1{T-2}\sum_{i=1}^T e_i^2=0$ 估计 $\sigma^2(e_i)$。（三个点才能求，所以自由度是 $T-2$）

方差分解

因为 $R_i=\alpha_i+\beta_i+e_i$ 且 $\mathrm{cov}(e_i,R_m)=0$，有：

\[\sigma_i^2=\beta_i^2\sigma_m^2+\sigma^2(e_i) \]

系统性风险 $\beta_i^2\sigma^2$，公司特有风险 $\sigma^2(e_i)$。

注意到，如果 $n$ 个不同资产，每个资产 $\frac 1n$，公司特有风险随着 $n$ 趋于无穷会趋于 $0$。

所以对于 $n$ 足够大的策略 $P$，有

\[R_p=\alpha_p+\beta_pR_m \]

于是

\[\sigma_p^2=\beta_p^2 \sigma_m^2 \]

资本定价模型（Capital Asset Pricing Model/ CAPM）

主要功能：

给出一个“公平的”期望收益率在给定风险之后
对尚未公开的资产的期望收益率的合理猜测

关键假设：投资者都是在无风险资产和市场风险资产之间自由组合。最优策略是市场策略。不能的投资者只是无风险资产和市场风险资产的比重不同。

设市场策略含有 $n$ 个证券，权值为 $w_1,\dots,w_n$。

$r_i$ 对 $r_m$ 的协方差为：

\[\sigma_{im}=\sum_{j=1}^nw_j\sigma_{ij}=w_1\sigma_{i1}+w_2\sigma_{i2}+\dots+w_n\sigma_{in} \]

市场策略的方差为：

\[\sigma_m^2=\sum_{i=1}^n\sum_{j=1}^n w_iw_j\sigma_{ij}=\sum_{i=1}^nw_i\sum_{j=1}^nw_j\sigma_{ij}=\sum_{i=1}^nw_i\sigma_{im} \]

所以，资产 $i$ 对 $\sigma_{m}^2$ 是 $w_i\sigma_{im}$，因此贡献占比为 $\frac{w_i\sigma_{im}}{\sigma_m^2}$。

类似的，可算出资产 $i$ 对 $E(r_m)-r_f$ 的贡献为 $w_i(E(r_i)-r_f)$，贡献占比为 $\frac{w_i(E(r_i)-r_f)}{E(r_m)-r_f}$。

关键假设：贡献风险高的资产贡献的收益率也大。

\[\frac{w_i\sigma_{im}}{\sigma_m^2}=\frac{w_i(E(r_i)-r_f)}{E(r_m)-r_f} \]

因此

\[E(r_i)=r_f+\frac{\sigma_{im}}{\sigma_m^2}(E(r_m)-r_f) \]

定义资产 $i$ 的 $\beta$ 为 $\beta_i=\frac{\sigma_{im}}{\sigma_m^2}$。

于是：

\[E(r_i)=r_f+\beta_i(E(r_m)-r_f) \]

CAPM 和 Index Models

注意到 CAPM 没有 $\alpha_i$，如果有正的 $\alpha$ 意味着无风险的收益，投资者就会买，价格就会提高，收益就会变少。

附录

考虑最优化问题

\[\max_w E(r_q)-\frac{1}{2}A\sigma_q^2\\ \]

其中 $r_q=r_f+y(r_p-r_f)$，$\sigma_q=y\sigma_p$。

等价于最优化：

\[\max_{w_1,\dots,w_n}r_f+\sum_{i=1}^n yw_i[E(r_i)-r_f]-\frac{1}{2}A\sum_{i=1}^n\sum_{j=1}^n(yw_i)(yw_j)\sigma_{ij}\\ \mathrm{s.t.} \sum_{i=1}^n w_i=1 \]

令 $\tilde{w_i}=yw_i$，等价于最优化：

\[\max_{\tilde{w_1},\dots,\tilde{w_n}}r_f+\sum_{i=1}^n\tilde{w_i}[E(r_f)-r_f]-\frac 12 A\sum_{i=1}^n\sum_{j=1}^n\tilde{w_i}\tilde{w_j}\sigma_{ij} \]

对 $\tilde{w_i}$ 求导，可得

\[0=E(r_i)-r_f-A\sum_{j=1}^n \tilde{w_j}\sigma_{ij}=E(r_i)-r_f-Ay\sigma_{iM},\forall i=1\dots n \]

乘上 $w_i$ 并累加：

\[w_i[E(r_i)-r_f]=Ayw_i\sigma_{iM}\\ E(r_M)-r_f=Ay\sigma_M^2 \]

所以也可以得到结论：

\[\frac{E(r_i)-r_f}{E(r_M)-r_f}=\frac{Ay\sigma_{iM}}{Ay\sigma_M^2}=\frac{\sigma_{iM}}{\sigma_M^2} \]

套利定价理论（Arbitrage Pricing Theory）

用来给衍生品定价。一个套利机会是构造一个 0 投资策略有固定收益。套利的收益率是 $+\infty$，风险是零。所以资产价格必须满足无套利（no arbitrage condition），这就是套利定价理论的关键假设。还有一个关键假设是公司固有风险可以被多样性稀释。

回忆 Index Model 有：

\[R_i=\alpha_i+\beta_iR_m+e_i \]

等价于：

\[r_i=r_f+\alpha_i+\beta_i(r_m-r_f)+e_i \]

求期望：

\[E(r_i)=r_f+\alpha_i+\beta(E(r_m)-r_f)+e_i \]

令 $F=r_m-E(r_m)$，于是 $E(F)=0$。两式相减得：

\[r_i=E(r_i)+\beta_iF+e_i \]

因此，对于一个策略 $P$ 有：

\[r_p=E(r_p)-\beta_pF+e_p \]

如果 $P$ 足够多样，$e_p=0$，可得：

\[r_p=E(r_p)+\beta_p F \]

有结论如果足够多样得策略 $P,Q$ 得 $\beta$ 相同，那么 $E(r_P)=E(r_Q)$。

证明：设 $\beta_P=\beta_Q$ 但 $E(r_P)>E(r_Q)$，无论 $F$ 是什么，$r_P=E(r_P)+\beta_PF>E(r_Q)+\beta_QF=r_Q$，因此可以做空 $Q$ 买入 $P$。

那如果 $\beta$ 不同呢？那可以用无风险资产稀释大的 $\beta$。

因此满足：

\[\frac{E(r_P)-r_f}{\beta_P}=\frac{E(r_Q)-r_f}{\beta_Q} \]

回忆以下，市场策略 $M$ 的 $\beta_M=1$，那么：

\[\frac{E(r_P)-r_f}{\beta_P}=\frac{E(r_m)-r_f}{1} \]

于是：

\[E(r_P)=r_f+\beta_P(E(r_m)-r_f) \]

这恰好就是 CAPM 模型！！！

CAPM 和 APT 的关系

CAPM 基于一分风险一分收益，APT 基于无套利等式 $\frac{E(r_P)-r_f}{\beta_P}=\frac{E(r_Q)-r_f}{\beta_Q}$。

CAPM 的 $\beta$ 是求出来的，为$\frac{\sigma_{im}}{\sigma_m^2}$，APT 的 $\beta$ 是基于 Index Model 的，是股票固有的。

债券（Bonds）

标准债券用发行人（Issuer），票息（coupon）和到期时间（Maturity）描述。

发行人：负责偿还债务的实体
票息：年利率。每半年支付一次
到期时间：债务到期，本金得到偿还的日期

一个债券的面值（Face value ）通常是 $\$1,000$，但价格以 $\$100$ 为单位报价。

收益率（Yield）

债券的报价基于收益率的概念，即基于当前价格和承诺现金流。

考虑一个 zero-coupon bond（ZCB）到期时间为 $t$ 年后，价格为 $P$，设收益率为 $y$，有：

\[P=\frac{100}{(1+y)^t} \]

这和债券预期收益有关，但不等同于预期收益。因为有风险，甚至美国国债到期前也有风险。

考虑一个 coupon bond，每半年会有票息 $c$，那么它的价值 $P$ 满足：

\[P/100=\frac{c/2}{(1+y/2)^1}+\frac{c/2}{(1+y/2)^2}+\dots+\frac{1+c/2}{(1+y/2)^{2T}} \]

当然，在某个时间买还会有时间相关折算，现在债券的实际价值称为全价（all-in(or dirty) price），从上次分红时间算的价值被称为净价（clean price），报价通常报的是净价。

公司债券

公司通过发行债券借钱，有一些在纽约证券交易所债券平台交易，大多数在场外交易。

可赎回债券（Callable bonds）：可在到期日之前回购
可转换债券（Convertible bonds）：可以换成公司的股票
可回卖债券（Puttable bonds）：给投资者延长债券到期时间的选择权
浮动利率债券（Floating-rate bonds）：票息可调整

利率的期限结构

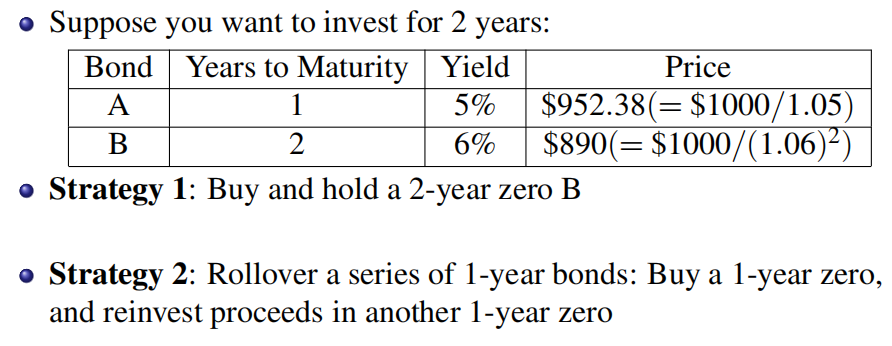
在无风险条件下，应该满足 $(1+y_2)^2=(1+r_1)(1+r_2)$，否则供需会不平衡，导致价格波动。其中：

$y_2$ 是 2-year yield to maturity -> 即期利率（spot rate）。
$r_1$ 是 1-year yield offered today -> 短期利率（short rate）today。
$r_2$ 是 1-year yield next year -> short rate next year。

一个即期利率是组成它的短期利率的几何平均。

\[(1+y_n)^n=(1+y_{n-1})^{n-1}(1+r_n)\\ 1+r_n=\frac{(1+y_n)^n}{(1+y_{n-1})^{n-1}} \]

未来的 short rate 是不确定的 -> 我们采用远期利率（forward interest rates）描述。

\[1+f_n=\frac{(1+y_n)^n}{(1+y_{n-1})^{n-1}} \]

通常会有 $f_n>E(r_n)$，这是因为有流动性溢价。如果 $f_n=E(r_n)$ 就是无流动性溢价。

股票估值（Equity Valuation）

假设持有了股票一年，价格从 $P_0$ 变化到了 $P_1$，和每股的分红 $D_1$。$P_1$ 和 $D_1$ 都是随机变量。

期望收益率：

\[E(r)=\frac{E(D_1)+E(P_1)-P_0}{P_0} \]

给出 $E(P_1)$ 和 $E(D_1)$ 的预测，我们可以估计 $E(r)$。

市场资本化率（Market Capitalization Rate）

回顾 CAPM：期望收益率和风险相关，风险用 $\beta$ 估量，高 $\beta$ 应该有高收益。$\beta$ 是 Index Model 中股票固有的属性。

结论是：

\[E(r)=r_f+\beta(E(r_m)-r_f) \]

市场资本化率 $k$ 是期望收益率（和 $\beta$ 相关）。

\[k=r_f+\beta(E(r_m)-r_f) \]

也被称为必要收益率（required rate of return）

注意这里的 $\beta$ 和 $k$ 都是和资产相关的，不同股票是不同的。

内在价值（Fundamental Value/Intrinsic value）

一个证券的内在价值是其期望收益率等于市场资本化率的价格。

例如，$\beta=1.25,E(r_m)=12\%,r_f=4\%$

那么：

\[k=r_f+\beta(E(r_m)-r_f)=4+1.25\times 8=14\% \]

如果 $E(P_1)=52,E(D_1)=4$，那么内在价值 $V_0$ 满足：

\[E(r)=\frac{56-V_0}{V_0}=0.14 \]

解得 $V_0=49.12$。

如果 $P_0=48$，那么这个证券被低估了（underpriced）。

股利贴现模型（The Dividend Discount Model）

根据定义：

\[k=\frac{D_1+P_1-V_0}{V_0} \]

可得：

\[V_0=\frac{D_1+P_1}{1+k} \]

其中 $D_1$ 是可预测的，$P_1$ 是不能的，但是可以假设 $P_1=V_1$（未来的内在价值）

那么

\[V_0=\frac{D_1}{1+k}+\frac{V_1}{1+k} \]

根据定义又有：

\[V_1=\frac{D_2+P_2}{1+k} \]

再设 $P_2=V_2$，以此类推可以得到：

\[V_0=\frac{D_1}{1+k}+\frac{D_2}{(1+k)^2}+\frac{D_3}{(1+k)^3}+\dots \]

这依然难以估计，因此有

固定增长股利贴现模型（The Constant Growth DDM）

假设股利逐年增长，增长率为 $g$。即 $D_{i+1}=D_i(1+g)$。那么内在价值 $V_0$ 只取决于 $k,g,D_1$。

令：

\[x=\frac{1+g}{1+k} \]

那么

\[V_0=\frac{D_1}{1+k}(1+x+x^2+\dots) \]

这里假设 $x<1$（暗含 $k>g$），有

\[V_0=\frac{D_1}{1+k}\frac{1}{1-x}=\frac{D_1}{k-g} \]

DDM 暗含了股价会增长如果：

股利增长
股利增长率增长
市场资本化率下降

一些讨论

DDM 是无意义的如果 $k<g$
如果一个股票永远不分红？资产泡沫。DDM 不适用。

多阶段 DDM（Multistage DDM）

Constant growth DDM 虽好，但不贴合实际，可以将股利分为多阶段，每段分别贡献。

市盈率（Price-Earnings Ratios）

设 $E_1$ 为每股期望收益在交税之后。收益要么保留，要么作为股息发放。

令 $b$ 为收益留存率（retention ratio/plowback ratio），$1-b$ 为 股利支付率。

期望分红为 $D_1=(1-b)E_1$，所以如果 $P_0$ 等于内在价值，会有：

\[P_0=\frac{D_1}{k-g}=\frac{(1-b)E_1}{k-g} \]

设一家公司资产全部为股权融资（负债为 $0$）。令 $\mathrm{ROE}$：return of equity。那么 $g=\mathrm{ROE}\times b$

结论是收益 $E_t$、分红 $D_t$、净值 $N_t$ 的增长率都为 $1+Rb$。

定义市盈率（Price-Earning Ratios/ P/E ratio）为：

\[\frac{P_0}{E_1}=\frac{1-b}{k-g} \]

意义是维持当前收益什么时候分到股票价值的钱。

P/E 取决于资产得到成长性，风险，留存比率 $b$。

期权（Options）

看涨期权（Call Option）使持有者获得在到期时间（或之前）以行权价格买入权。

看跌期权（Put Option）使持有者获得在到期时间（或之前）以行权价格卖出权。

期权买入者（holder）有权利买入/卖出证券，卖出者（writer）有义务买入/卖出证券。

美式期权（American option）是允许在到期时间之前行权，欧式期权（European option）只能在到期日行权。

实值期权（in the money）是指现在行权有收益的，否则称为 虚值期权（out of the money）。

保证金（Margin）和清算（Clearing）机制

期权的 writer 必须缴纳保证金，卖出看涨期权的一方价格上涨可能触发追加保证金，卖出看跌期权的一方价格下跌可能触发追加保证金。

抛补看涨期权（Covered Call）

买入股票，卖出看涨期权

保护看跌期权（Protective Put）

买入股票，买入看跌期权

复制原理（Principle of Replication）

如果两个资产在未来所有的支付结构相同，那么它们的价格相同。

设行权价格 $X$，Call 的价格为 $C$，Put 的价格为 $P$。

那么有买股票加买看跌期权等价于买看涨期权加未来的 $X$ 元。

所以有：

\[S_0+P=C+\frac{X}{(1+r_f)^T} \]

$T$ 是 $T$ 年之后。

期权定价（Options Pricing）

如何定价期权呢，现在给出二叉树模型，股票价格加个经过一段时间后只有两种可能，两种可能记作 $+$ 和 $-$，无风险利率为 $8\%$。

例如，股票现在价格 $S=100$，一个月后可能是 $S^+=200$ 也可能是 $S^-=50$，要算行权价格 $125$ 的看涨期权价值。

那么一个月后期权的价值为 $C^+=75$ 和 $C^-=0$。

一个杠杆股票投资组合为，买一股然后借未来的 50 美元，等价于现在的 $50/1.08$ 美元，然后这个组合的价值为 $100-50/1.08=53.7$。

这样一个月后这个组合的现金流等于 $2C$ 的现金流（$+$ 时为 $200-50=150$ 美元，$-$ 时为 $50-50=0$），因此 $2C=53.7$，可解得 $C$ 的价值。

如果是不止一层的二叉树，先算孩子价值，然后算当前点。

对冲比率：

\[H=\frac{C^+-C^-}{S^+-S^-} \]

买 $H$ 单位股票，买 $1$ 单位 $C$，再借一些钱，可对冲出无风险策略，收益率 $=r_f$。

期货（Futures）

现货-期货平价定理（Spot-Futures Parity Theorem）

下面两种获取未来资产方式价值是相等的

买入并且存储（要考虑存储成本等成本）
建立多头头寸

否则可以套利。

考虑如下策略：

买入一个单位指数基金，建立空头头寸，价值为 $F_0$。

过了一年之后，设分红是 $D$。

那么有收益率是 $r_f$：

\[\frac{(F_0+D)-S_0}{S_0}=r_f \]