原文地址
Floating point numbers — Sand or dirt
Floating point numbers are like piles of sand; every time you move them around, you lose a little sand and pick up a little dirt. — Brian Kernighan and P.J. Plauger
Real numbers are a very important part of real life and of programming too. Hardly any computer language doesn’t have data types for them. Most of the time, they come in the form of (binary) floating point datatypes, since those are directly supported by most processors. But these computerized representations of real numbers are often badly understood. This can lead to bad assumptions, mistakes and errors as well as reports like: "The compiler has a bug, this always shows ‘not equal’"
1 2 3 4 5 6 7 8 9 |
var
F: Single;
begin
F := 0.1;
if F = 0.1 then
ShowMessage('equal')
else
ShowMessage('not equal');
end;
|
Experienced floating point users will know that this can be expected, but many people using floating point numbers use them rather naively, and they don’t really know how they “work”, what their limitations are, and why certain errors are likely to happen or how they can be avoided. Anyone using them should know a little bit about them. This article explains them from my point of view, i.e. things I found out the hard way. It may be slightly inaccurate, and probably incomplete, but it should help in understanding floating point, its uses and its limitations. It does not use any complicated formulas or higher scientific explanations.
Floating point types in Delphi
Floating point is the internal format in which “real” numbers, like 0.0745 or 3.141592 are stored. Unlike fixed point representations, which are simply integers scaled by a fixed amount — an example is Delphi’s Currency type — they can represent very large and very tiny values in the same format. While Delphi knows several types with differing precision, the principles behind them are (almost) the same. The types Single, Double and Extended are supported by the hardware (by the FPU — floating point unit) of most current computers and follow the IEEE 754 binary format specs. The type Real, which is a relict of old Pascal, now maps to Double by default, but, if you set {$REALCOMPATIBILITY ON}, it maps to Real48 type, which is not an IEEE type and used to be managed by the runtime system, that is, in software, and not by hardware. There is also a Comp type, but this is in fact not a floating point type, it is an Int64 which is supported and calculated by the FPU.
The Real48 type is pretty obsolete, and should only be used if it is absolutely necessary, e.g. to read in files that contain them. Even then it is probably best to convert them to, say, Double, store those in a new file and discard the old file.
While Real types used to be managed in software, for computers that did not have an FPU (which was not uncommon in the earlier days of Turbo Pascal), this is not the case for current systems, which have an FPU. The runtime converts Real48 to Extended, uses that to do the required calculations and then converts the result back to Real48. This constant conversion makes the type pretty slow, so you should really, really avoid it.
Note that the above does not apply to Real, if it is mapped to Double, which is the default setting. It only applies to the 6-byte Real48 type.
Real numbers
The real-number system is a continuum containing real values from minus infinity (−∞) to plus infinity(+∞). But in a computer, where they are only represented in a very limited amount of bytes (Extended, the largest floating point type in Delphi, has no more than 80 bits and the smallest, Single, only 32!), you can only store a limited amount of discrete values, so it is not nearly a continuum. Most real numbers can only (roughly) be approximated by floating point types. Everyone using them should always be aware of this.
There are several ways in which real numbers can be represented. In written form, the usual way is to represent them as a string of digits, and the decimal point is represented by a ‘.’, e.g. 12345.678 or 0.0000345. Another way is to use scientific notation, which means that the number is scaled by powers of 10 to, usually, a number between 1 and 10, e.g. 12345.678 is represented as 1.2345678 × 104 or, in short form (the one Delphi uses), as 1.2345678e4.
Internal representation
The way such "real" numbers are represented internally differs a bit from the written notation. The fixed point type Currency is simply stored as a 64 bit integer, but by convention its decimal point is said to be 4 places from the right, i.e. you must divide the integer by 10000 to get the value it is supposed to represent. So the number 3.76 is internally stored as 37600. The type was meant to be used for currencies, but that the type only has 4 decimals means that calculations other than addition or subtraction can cause inaccuracies that are often not tolerable.
The floating point types used in Delphi have an internal representation that is much more like scientific notation. There is an unsigned integer (its size in bit depends on the type) that represents the digits of the number, the mantissa, and a number that represents the scale, in our case in powers of 2 instead of 10, the exponent. There is also a separate sign bit, which is 1 if the number is negative. So in floating point, a number can be represented as:
value = (−1)sign × (mantissa / 2len−1) × 2exp
where sign is the value of the sign bit, mantissa is the mantissa as unsigned integer (more about this later), len is the length of the mantissa in bits, and exp is the exponent.
Mantissa
The mantissa (The IEEE calls it “significand”, but this is a neologism which means something like “which is to be signified”, and in my opinion, that doesn’t make any sense) can be viewed in two ways. Let’s disregard the exponent for the moment, and assume that its value is thus that the number 1.75 is represented by the mantissa. Many texts will tell you that the implicit binary point is viewed to be directly right of the topmost bit of the mantissa, i.e. that the topmost bit represents 20, the one below that 2−1, etc., so a mantissa of binary 1.1100 0000 0000 000 represents 1.0 + 0.5 + 0.25 = 1.75.
Other, but not so many texts, simply treat the mantissa as an unsigned integer, scaled by 2len−1, where len is the size of the mantissa in bits. In other words, a mantissa of 1110 0000 0000 0000 binary or 57344 in decimal is scaled by 215 = 32768 to give you 57344 / 32768 = 1.75 too. As you see, it doesn’t really matter how you approach it, the result is the same.
Exponent
The exponent is the power of 2 by which the mantissa must be multiplied to get the number that is represented. Internally, the exponent is often “biased”, i.e. it is not stored as a signed number, it is stored as unsigned, and the extremes often have special meanings for the number. This means that, to get the actual value of the exponent, you must subtract a constant value from the stored exponent. For instance, the bias for Single is 127. The value of the bias depends on the size of the exponent in bits and is chosen thus, that the smallest normalized value (more about that later) can be reciprocated without overflow.
There are also floating point systems that have a decimal based exponent, i.e. where the value of the exponent represents powers of 10. Examples are the Decimal type used in certain databases and the — slightly incompatible — Decimal type used in Microsoft .NET. The latter uses a 96 bit integer to represent the digits, 1 bit to represent the sign (+ or −) and 5 bits to represent a negative power of 10 (0 up to 28). The number 123.45678 is represented as 12345678 × 10−5. I have written an almost exact native copy of the Decimal type to be used by Delphi. It is a little faster than the original .NET type, but not nearly as fast as the hardware supported types.
This article mainly discusses the floating point types used in Delphi, to know Single, Double and Extended, which are all floating binary point types. Floating decimal point types like Decimal are not supported by the hardware or by Delphi. So if, in this article, I speak of "floating point" I mean the floating binary point types.
Sign bit
The sign bit is quite simple. If the bit is 1, the number is negative, otherwise it is positive. It is totally independent of the mantissa, so there is no need for a two’s complement representation for negative numbers. Zero has a special representation, and you can actually even have −0 and +0 values.
Normalization and the hidden bit
I’ll try to explain normalization and denormals with normal scientific notation first.
Take the values 6.123 × 10−22, 612.3 × 10−24 and 61.23 × 10−23 (or 6.123e-22, 612.3e-24 and 61.23e-23 respectively). They all denote the same value, but they have a different representation. To avoid this, let’s make a rule that there can only be one (non-zero) digit to the left of the decimal point. This is called normalization. Something similar is done with binary floating point too. Since this is binary, there is only one digit left: 1. So there can only be one (non-zero) digit (always 1) to the left of the binary point. Since this is always the same digit, it does not have to be stored, it can be implied. This is the so-called hidden bit. The types Single and Double do not store that bit, but assume it is there in calculations.
How is this done in binary? Let’s take the number 0.375. This can be calculated as 2−2 + 2−3 (0.25 + 0.125), or, in a mantissa, 0.011…bin (disregarding the trailing zeroes), i.e. 0.375 × 20. But this is not how floating point numbers are usually stored. The exponent is adjusted thus, that the mantissa always has its top bit set, except for some special numbers, like 0 or the so called “tiny” (denormalized) values. So the mantissa becomes 1.100…bin and the exponent is decremented by 2. This number still represents the value 0.375, but now as 1.5 × 2−2. This is how normalization works for binary floating point. It ensures that 1.0 <= mantissa (including hidden bit) < 2.0. Because of the hidden bit, to calculate the value of such a floating point type, you must mentally put the implicit “1.bin” in front of the stored bits of the mantissa.
Note that in e.g. the language C, the value FLT_MIN stands for the smallest (positive) normalized value. You can have values smaller than that, but they will be denormal values, i.e. with a lower precision than 24 bits.
There is some confusion about how to denote the size (or length, as it is often called) of the mantissa of a type with a hidden bit. Some will use the actually stored length in bits, while others also count the hidden bit. For instance, a Single has 23 bits of storage reserved for the mantissa. Some will call the length of the mantissa 23, while others will count the hidden bit too and call it a length of 24.
Denormalized values
With real numbers, to get close to zero, you can simply use a very negative exponent, e.g. 6.123 × 10−99999. But in floating point, the exponent is limited and can not go below a certain value. The mantissa is limited too. Let’s assume that in our scientific notation, the exponent can not go below −100 and the mantissa can only have 4 digits. Then a very small normalized value would be 6.123 × 10−100. To denote even smaller values, you have to resort to denormals: you drop the rule that the first digit must always be non-zero. Now you can also have values smaller than the smallest normalized (positive) value of 1.000 × 10−100, like 0.612 × 10−100, 0.061 × 10−100 and 0.006× 10−100. This also means that the lower you go, you lose precision: fewer and fewer significant digits are available.
This is similar for binary floating point, except that the digits are just 0 or 1. Sometimes, after an operation, the exponent can not be decremented far enough to represent the result. In that case, the exponent is set to a special value, and the mantissa is not normalized anymore, i.e. the top bit is not 1 and the mantissa is interpreted as something like 0.000xxx…xxxbin, i.e. it has one or more leading zeroes followed by as many significant bits as will fit. Such values are called denormalized or tiny values. Because of the leading zeroes, not every bit is significant anymore, so the precision is lower than for normalized values of the same type.
Other special values
The most obvious special value is 0. Because 0 is denoted by both exponent and mantissa having all zero bits, there are actually two representations of 0, one with the sign bit cleared, and one with the sign bit set (i.e. +0 and −0). In any calculation, these are considered equal and simply represent 0.
Not every bit combination represents a number. Some represent +/− infinity, and some are invalid. The latter are called NaN — Not a Number. The rules for which bit combinations represent what are described in the Delphi help, and in the Delphi DocWiki: Single, Double and Extended. I will not repeat that information here. But the Math unit contains a few constants and functions that can help you check or assign some of these values:
1 2 3 4 5 6 7 8 9 10 11 12 |
const
NaN = 0.0 / 0.0;
Infinity = 1.0 / 0.0;
NegInfinity = -1.0 / 0.0;
function IsNan(const AValue: Double): Boolean; overload;
function IsNan(const AValue: Single): Boolean; overload;
function IsNan(const AValue: Extended): Boolean; overload;
function IsZero(const A: Extended; Epsilon: Extended = 0): Boolean; overload;
function IsZero(const A: Double; Epsilon: Double = 0): Boolean; overload;
function IsZero(const A: Single; Epsilon: Single = 0): Boolean; overload;
|
IEEE types
The IEEE types used in Delphi are
| Type | Mantissa bits | Exponent bits | Sign bit | Smallest value | Biggest value | Exponent Bias | |
|---|---|---|---|---|---|---|---|
| Single | 0-22 | 23-30 | 31 | 1.5 × 10−45 | 3.4 × 10+38 | 127 | |
| Double | 0-51 | 52-62 | 63 | 5.0 × 10−324 | 1.7 × 10+308 | 1023 | |
| Extended | 0-63 | 64-78 | 79 | 3.4 × 10−4951 | 1.1 × 10+4932 | 16383 | no hidden bit |
The following diagram shows a simple representation of these types:
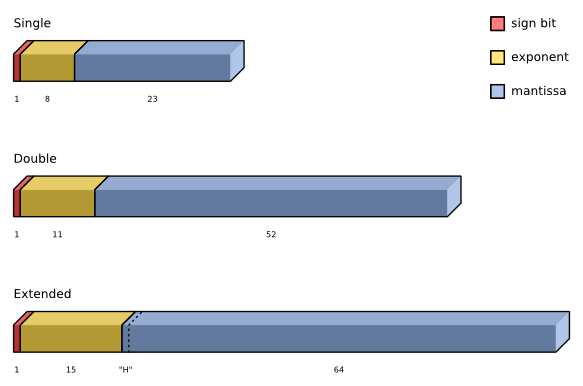
Due to how floating point is implemented on Win64 (using SSE instead of the x87 FPU), there is no 80-bit floating point type in the 64-bit compiler. That is why, on Win64, Delphi’s Extended is aliased to the 64-bit type Double.
Using floating point numbers
Nothing brings fear to my heart more than a floating point number. — Gerald Jay Sussman
In the following, I am using the terms small and large. I mean values that have a very low or a very high exponent, respectively, regardless of their sign. That means that small values are very close to 0, while large values are far away from 0. In other words, I am addressing their magnitude, not their signs.
As you can see in the diagram, the different types have quite a different precision. Internally, for calculations, Delphi always uses Extended. Literals, like 0.1 are also stored as Extended. That is why the little code snippet at the beginning of this article produced False, since it was converted from Extended to Single, losing a few bits of precision, and for the comparison, it was converted back to Extended. The loss of precision caused the difference, so the result of the comparison was False.
There are many such traps, caused by the limitations of how the infinite range of real numbers must be represented in a finite number of bits. Some of these traps are discussed in the following paragraphs.
Rounding
After calculations, e.g. multiplications or additions, the result can contain more significant bits than the type can hold, so the FPU must round the values to make them fit and normalized again, which means that a number of bits gets lost. How this rounding is done is governed by IEEE rules. But this means that there will be additional tiny inaccuracies. An example:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
program Project1;
{$APPTYPE CONSOLE}
var
S1, S2: Single;
begin
S1 := 0.1;
Writeln(S1:20:18);
S1 := S1 * S1;
S2 := 0.01;
Writeln(S1:20:18);
Writeln(S2:20:18);
Readln;
end.
|
The output is
0.100000001490116120 0.010000000707805160 0.009999999776482580
As you can see, the closest possible representation for 0.1 in a Single is 0.10000000149011612. If this is squared and then rounded, you get 0.01000000070780516, but the closest representation for 0.01 is 0.00999999977648258. So, in other words, Single(0.1) * Single(0.1) <> Single(0.01).
Doing multiple calculations like this will slowly add up the errors, and they do not necessarily even each other out. It is very important that you take such errors into consideration and do no more calculations than necessary. It is always a good idea to simplify your expressions and to use professional libraries that know how to avoid too many calculations for the purpose. As in so many programming problems, the choice of algorithm and of the used types is also very important.
Rounding modes and tie-breaking rules
Rounding is generally done to the nearest more significant digit available. But sometimes there is a tie, if the value to be rounded is exactly between the two nearest digits. In that case, a tie-breaking rule is required and one very common rule is called banker’s rounding (although banks are not known to use or having used it), which says that a tie is rounded to the nearest even more significant digit. This means that 24.05 is rounded to 24.0, but 24.15 to 24.2.
Other commonly used tie-breaking rules are:
- Truncating (towards 0) — This means that 24.05 is rounded to 24.0, and −24.05 to −24.0. In fact, the less significant digits are simply dropped.
- Rounding up (towards +∞) — This means that 24.05 is rounded to 24.1, but −24.05 to −24.0. This mode is taught in many schools.
- Rounding down (towards −∞) — This means that 24.05 is rounded to 24.0, and −24.05 to −24.1.
- Rounding away from 0 — This means that 24.05 is rounded to 24.1, and −24.05 to −24.1. This mode is taught in many schools too, but is not an IEEE approved method.
Note that there are other rounding modes that do not round to the nearest more significant digit, but round to the more significant digit that is either above (closer to +∞), below (closer to −∞) or closer to 0.
RoundTo and SimpleRoundTo
Unit math contains a few nice functions to round a floating point value (Extended) to a set number of digits:
1 2 3 4 5 6 7 8 9 10 11 |
type
TRoundToRange = -37..37;
TRoundToEXRangeExtended = -20..20;
function RoundTo(const AValue: Extended;
const ADigit: TRoundToEXRangeExtended): Extended;
{ This variation of the RoundTo function follows the asymmetric arithmetic
rounding algorithm (if Frac(X) < .5 then return X else return X + 1). This
function defaults to rounding to the hundredth's place (cents). }
function SimpleRoundTo(const AValue: Extended; const ADigit: TRoundToRange = -2): Extended;
|
RoundTo is probably a little more accurate and faster, but SimpleRoundTo allows a bigger range of digits and uses a slightly different rounding algorithm.
For better decimal rounding than these rather simple approaches, take a look at John Herbster’s DecimalRounding_JH1 unit on Embarcadero’s CodeCentral. It uses a more sophisticated algorithm which produces better results. It implements all the rounding modes I discussed in the Rounding modes and tie-breaking rules section above.
The x87 Floating Point Unit
The x87 FPU knows 4 rounding modes (see the FPU control word section of this article). So how does the FPU round? Say an operation on a Single produced an intermediate result that has some extra low bits. The extended mantissa looks like this:
1.0001 1100 0100 1100 1001 0111
The underlined bit is the bit to be rounded. There are two possible values this can be rounded to, the value directly below and the value directly above:
1.0001 1100 0100 1100 1001 011
1.0001 1100 0100 1100 1001 100
Now what happens depends on the rounding mode. If the rounding mode is the default — round to nearest “even” — it will get rounded to the value that has a 0 as least significant bit. You can probably guess which of the two values is chosen for the other rounding modes.
Measuring rounding errors
There are ways to measure accumulated rounding errors. The most common methods used are ULP and relative or approximation error. Discussing them is outside the realm of this article, so I have to refer you to Wikipedia and the articles mentioned in the References section of this article.
Conversion
It is never a good idea to write code that requires a lot of
conversions, for instance code that must convert between several
floating point types, since each conversion, especially to a less
precise type, can mean the loss of a few bits and therefore increases
the inaccuracy. If space or speed are not as important as accuracy, use
the Extended type throughout, because Delphi also uses it internally in most system functions. An example:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
program Project2;
{$APPTYPE CONSOLE}
var
S: Single;
E: Extended;
begin
E := 0.1;
Writeln(E:20:18);
S := E;
E := S;
Writeln(E:20:18);
Readln;
end.
|
The output is:
0.100000000000000000 0.100000001490116120
Literals
In source code, we use decimal numbers. But floating point types are stored as binary. For integers, this is not a big problem, but as soon as fractions are involved, there is one. Not every number that can be represented exactly in decimal can be represented exactly in binary, just like certain numbers, e.g. 1/3 or π can not be represented exactly in decimal format. In binary, only numbers that are sums of powers of 2 can be represented exactly in a binary floating point type (e.g. 3.625 = 2 + 1 + 0.5 + 0.125). A number like 0.1 can not be composed of such powers. The compiler will try to get the best approximation that is possible, but there will always be a small difference.
Comparing values
The above shows that it is never a good idea to compare floating point values directly. Conversions and rounding cause tiny inaccuracies. These errors can add up, the more calculations you do.
To accomodate for these inaccuraries, it is a good idea to always use a small error value in comparisons. In Delphi’s Math unit, there are a number of of overloaded functions that can help you do that:
1 2 3 4 5 6 7 |
function CompareValue(const A, B: Extended; Epsilon: Extended = 0): TValueRelationship; overload;
function CompareValue(const A, B: Double; Epsilon: Double = 0): TValueRelationship; overload;
function CompareValue(const A, B: Single; Epsilon: Single = 0): TValueRelationship; overload;
function SameValue(const A, B: Extended; Epsilon: Extended = 0): Boolean; overload;
function SameValue(const A, B: Double; Epsilon: Double = 0): Boolean; overload;
function SameValue(const A, B: Single; Epsilon: Single = 0): Boolean; overload;
|
An ε (epsilon) value is a small value you can use as an error range. These functions either take an ε you provide, or if you pass nothing or 0, they will calculate an ε that takes the magnitude of the operands you are comparing into consideration. So it is usually best only to pass the operands, and not a specific ε, unless you have a really good reason to force one upon the function. An example follows:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 |
program Project3;
{$APPTYPE CONSOLE}
uses
SysUtils, Math;
var
S1, S2: Single;
begin
S1 := 0.3;
S2 := 0.1;
S2 := S2 / 10.0; // should be 0.01
S2 := S2 * 10.0; // should be 0.1 again
S2 := S2 + S2 + S2; // should be 0.3
if S1 = S2 then
Writeln('True')
else
Writeln('False');
if SameValue(S1, S2) then
Writeln('True')
else
Writeln('False');
Readln;
end.
|
The output is
False True
That is because S1 has the value 0.300000011920928955078125, while the calculation resulted in S2,
- which started out as 0.100000001490116119384765625,
- then, after the division, became 0.00999999977648258209228515625
- and after the multiplication 0.0999999940395355224609375.
- Adding this value twice more resulted in 0.2999999821186065673828125.
(Exact values extracted using my ExactFloatString unit)
SameValue accounts for the little differences, while = compares for exact equality.
Catastrophic cancellation
If almost equal values are subtracted (or two values with differing sign but otherwise almost equal values are added), the result is a value that is tiny, compared to the values. This tiny value can well be in the range of the roundoff errors mentioned before, so it can’t be trusted. It is another situation you should avoid. An example follows:
1 2 3 4 5 6 7 8 9 |
procedure Test;
var
E1, E2, E3: Extended;
begin
E1 := 16.000000000000000001;
E2 := 16.000000000000000000;
E3 := E1 - E2;
Writeln(E1:22:18, E2:22:18, E3);
end;
|
The output from Delphi 2010 is:
16.000000000000000000 16.000000000000000000 1.73472347597681E-0018
One would expect the difference to be 1.0 × 10−18, but the value you get is 1.735 × 10−18.
Also note that the output doesn’t display the decimal 1 in E1, which shows you can’t always trust the accuracy of your output either.
This is an example of catastrophic cancellation: a devastating loss of precision when small numbers are computed from large numbers, which themselves are subject to roundoff error.
Greatly differing magnitude
This is more or less the reverse of catastrophic cancellation.
If two values differ greatly in magnitude, the smaller of the two might be below the precision of the larger one. So adding the tiny value to such a huge value (or subtracting it) will have no effect. That means that you should take care in which order you do such additions or subtractions. Take the following simple example:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
program Project4;
{$APPTYPE CONSOLE}
var
S1, S2, S3: Extended;
begin
S1 := 1000000000000000000000000.0; // S1 := 1e24;
S2 := -S1;
S3 := 1.0;
Writeln((S1 + S2) + S3:10:10);
Writeln(S1 + (S2 + S3):10:10);
Readln;
end.
|
The results shown are:
1.0000000000 0.0000000000
The first result is what you would expect, but the second one is the result of the fact that S3 got swallowed by the precision of the large value in S2, so here, S2 + S3 = S2. In mathematics, addition is associative
(a + b) + c = a + (b + c)
But the addition of floating point values is not associative, so
(a + b) + c ≠ a + (b + c)
Note that if you have many values to add, it makes sense to sort them in order of magnitude. A nice explanation is given to this StackOverflow question, by Steve Jessop. Be sure to read the comments too.
It comes down to the fact that if you add a tiny number to a big one, the tiny one may not change the big one, but if you add a lot of tiny ones first, they may accumulate to a value that can make a difference by being closer to the big one. The link gives some examples.
Also note the answer recommending the Kahan summation algorithm, by Daniel Pryden. Kahan’s algorithm sums the rounding errors in an extra floating point variable and uses that to get a more correct answer.
Functions requiring real values
Not only are fractions like 0.1 not representable in binary floating point, there are also values that are not representable in any integral number base, like the irrational numbers π or Euler’s constant e, but also values like √2. Functions based on numbers like these are bound to be inaccurate, especially in a limited format like floating point and because they require multiple internal calculations, even if these are probably with greater precision. That is why functions calls like sin(π) do not deliver exact results. For Sin(Pi), Delphi returns −5.42101086242752 × 10−20, instead of the expected 0.
Avoiding the traps
There are a few tips to avoid the many traps.
- Never forget that Delphi’s floating point types store in binary, and that often can’t represent decimal values accurately.
- Choose the right precision for your application.
- Do not mix several types of floating point.
- Be aware of rounding errors and that they can add up.
- Optimize and simplify your algorithms to avoid too many calculations.
- Use professional libraries instead of cooking your own ones.
- Do not add or subtract values of greatly differing magnitude (be aware of the risk of catastrophic cancellation).
- Do not compare values directly, but use library functions like
SameValue.
Internals
So how does this look internally? In the following example I use a Single, because Singles have a readily comprehensible number of bits in the mantissa and exponent. Let me show you how a number like 0.1 is stored in a Single.
The number
0.1
is stored as
$3DCCCCCD or (binary) 0011 1101 1100 1100 1100 1100 1100 1101
After ordering the bits, this is:
0 - 0111 1011 - 100 1100 1100 1100 1100 1101
which means
- the sign bit is 0,
- the exponent is 123 − 127 = −4 and
- the mantissa is (incl. hidden bit) 1100 1100 1100 1100 1100 1101 or $CCCCCD or 13421773.
If 13421773 is multiplied with 2−4 (0.0625), the result is 838860,8125. After scaling that by 223 (8388608), this becomes 0.100000001490116119384765625, which is indeed pretty close to 0.1. The following table shows that this is indeed the closest value, by also calculating the values with one ULP difference, i.e. with mantissas $CCCCCC and $CCCCCE respectively.
| Hex | Value | Difference with 0.1 (abs) |
|---|---|---|
| $3DCCCCCC | 0.0999999940395355224609375 | 0.0000000059604644775390625 |
| $3DCCCCCD | 0.100000001490116119384765625 | 0.000000001490116119384765625 |
| $3DCCCCCE | 0.10000000894069671630859375 | 0.00000000894069671630859375 |
To see how the conversion from text to binary is done (well, more or less), take a look at this StackOverflow answer of mine.
In reality, the functions that convert from a string in decimal format to binary floating point are very complicated. The de facto standard C implementation, strtod, by David M. Gay, uses several different algorithms, depending on the value. One of these algorithms even requires a simple implementation of an unlimited precision BigInteger. So it is, in many cases, not nearly as simple as in my Stack Overflow answer mentioned above.
My BigDecimal implementation can do extemely accurate conversions between decimal format strings like '1.34567e-138' and binary floating point types too (both ways), using BigDecimal as an intermediate representation.
The FPU control word
The FPU control word is a word-size set of bits that control the behaviour of the FPU. The bits are set up as follows
| Bits | Name | Values | Description |
|---|---|---|---|
| Exception flag masks | |||
| 0 | IM | 1 | Invalid operation |
| 1 | DM | 1 | Denormalized operand |
| 2 | ZM | 1 | Zero divide |
| 3 | OM | 1 | Overflow |
| 4 | UM | 1 | Underflow |
| 5 | PM | 1 | Precision |
| Precision bits | |||
| 8, 9 | PC | 00 | Single precision (24 bit mantissa) |
| 10 | Double precision (53 bit mantissa) | ||
| 11 | Extended precision (64 bit mantissa) | ||
| 01 | reserved | ||
| Rounding mode | |||
| 10, 11 | RM | 00 | Round to nearest even (banker’s rounding) |
| 01 | Round down toward infinity | ||
| 10 | Round up toward infinity | ||
| 11 | Round toward zero (trunc) | ||
| Infinity control | |||
| 12 | X | Used for compatibility with 287 FPU | |
| 0 | Projective | ||
| 1 | Affine | ||
| 6, 7, 13, 14, 15 | reserved and not used. | ||
| $133F turns off all exceptions | |||
In Delphi, to control the FPU control word (in Delphi, it is called 8087CW), there are a few functions, mentioned in the help and the DocWiki entry for the FPU Control Word. An example of their use:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
var
S1: Single;
S2: Single;
S3: Single;
begin
SetExceptionMask(GetExceptionMask + [exZeroDivide]); // default is: unmasked
try
S1 := 1.0;
S2 := 0.0;
S3 := S1 / S2;
except
on E: Exception do
Writeln(E.ClassName, ': ', E.Message);
end;
Writeln(S3);
end.
|
There is no exception, since including exZeroDivide will mask the division by zero FPU exception, this means that dividing by zero will not cause such an exception anymore. The result is +∞ instead.
Investigating floating point types
If you want to investigate or (ab)use the internal formats of the floating point types a little more, you should look for the routines by John Herbster, former member of TeamB. Most of them can be found on Embarcadero’s CodeCentral.
- DecimalRounding
- IEEE Number Analyzer
- ExactFloatToStr_JH0 — Exact Float to String Routines
- Mixed Binary-fraction Formating
- Mixed Fraction Encoder and Decoder
But also take a look at my (new) ExactFloatStrings unit, which is included with my BigIntegers unit. It works in Delphi XE3 up to Delphi 10 Seattle. I am working on making it work in Delphi XE2 too.
Also note that from Delphi XE3 on, you can use the helpers for floating point types, by including the System.SysUtils unit in your uses clause. For instance, to access the mantissa and exponent of a Double, you can do something like:
1 2 3 4 5 6 7 8 9 10 11 12 |
uses
System.SysUtils;
...
var
E: Integer;
M: UInt64;
D: Double;
begin
D := 1.1e-8;
M := D.Mantissa;
E := D.Exponent;
...
|
Basic conversions of floating point values…
… to their composite parts
There are a few basic functions that can be useful to examine the composing parts of a floating point value:
| Function | Unit | Output |
|---|---|---|
Int |
Math |
Returns the integral part (i.e. the part before the decimal point) of a floating point value as Extended. |
Frac |
System |
Returns the fractional part (i.e. the part after the decimal point) of a floating point value as Extended. |
Sign |
Math |
Returns the sign of a number value as TValueSign. |
Frexp |
Math |
Procedure that returns the mantissa and the exponent of a Double value as Extended and Integer, respectively. |
FloatToDecimal |
SysUtils |
Procedure that returns the composing parts of a floating point value in a TFloatRec as data that can be used for formatting. |
… to integers
To convert floating point values to Integers, there are a few system functions which each convert their numbers a little differently.
| Function | Unit | Output |
|---|---|---|
Trunc |
System |
Rounds a floating point value to the Int64 value nearest to zero (i.e. it truncates toward 0). |
Round |
System |
Rounds a floating point value to the nearest Int64 value, or when it is exactly halfway, uses “Banker’s rounding”. |
Floor |
Math |
Rounds a floating point value to the highest Int64 value that is less than or equal to it (i.e., it truncates toward −∞). |
Ceil |
Math |
Rounds a floating point value to the lowest Int64 value that is greater than or equal to it (i.e., it truncates toward +∞). |
These functions generally issue an EInvalidOp exception if the result would be outside the Int64 range.
… to and from text
To display a floating point number, the runtime must convert them from binary back to decimal. Also here, inaccuracies can creep in. It is also important what kind of format you choose. The specific output may depend on the format settings for the current locale, too.
The runtime library, especially the SysUtils unit, provides you with some convenient functions to format such numbers, like Format, FormatFloat, FloatToStrF, FloatToText and FloatToTextFmt. Take a look at FloatToDecimal as well.
The other way around, conversion from text to floating point, has some limitations. In Win32, a routine like StrToFloat internally uses Extended, so any Double or Single values resulting from this will be accurate. Unfortunately, this is not true in Win64. In Win64, the result of StrToFloat for large values (e.g. -1.79e30) can be off by one (lowest) bit, because internally, it uses Double for the conversion, and somehow the rounding is seems to be slightly inaccurate. For most practical purposes, this is not really a problem, but in some cases it can be.
Note that in C++Builder, a routine like strtod() is even slightly more inaccurate. I have found differences of two lowest bits.
Conclusion
Floating point types are useful, but one must be aware of their limitations. I hope this article helped you understand them a little better. But there are certainly things I forgot to mention, or which are incorrect. I am grateful for any constructive remark, criticism, objection, etc. You can contact me by e-mail to tell me what you think of this.
Rudy Velthuis


 浙公网安备 33010602011771号
浙公网安备 33010602011771号