实验二
作业信息
一、实验目的
- 理解K-近邻算法原理,能实现算法K近邻算法;
- 掌握常见的距离度量方法;
- 掌握K近邻树实现算法;
- 针对特定应用场景及数据,能应用K近邻解决实际问题。
二、实验内容
- 实现曼哈顿距离、欧氏距离、闵式距离算法,并测试算法正确性。
- 实现K近邻树算法;
- 针对iris数据集,应用sklearn的K近邻算法进行类别预测。
- 针对iris数据集,编制程序使用K近邻树进行类别预测。
三、实验报告及要求
- 对照实验内容,撰写实验过程、算法及测试结果;
- 代码规范化:命名规则、注释;
- 分析核心算法的复杂度;
- 查阅文献,讨论K近邻的优缺点;
- 举例说明K近邻的应用场景。
四、实验过程
1、实现曼哈顿距离、欧氏距离、闵式距离算法,并测试算法正确性。
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
|
import mathfrom itertools import combinations#1.计算欧式距离#p = 1 曼哈顿距离#p = 2 欧氏距离#p = inf 闵式距离minkowski_distancedef L(x, y, p=2):# x1 = [1, 1], x2 = [5,1] if len(x) == len(y) and len(x) > 1: sum = 0 for i in range(len(x)): sum += math.pow(abs(x[i] - y[i]), p) return math.pow(sum, 1/p) else: return 0 #2. 数据准备x1 = [1, 1]x2 = [5, 1]x3 = [4, 4]#3. 输入数据for i in range(1, 5): r = {'1-{}'.format(c):L(x1, c, p = i) for c in [x2, x3]}#字典 print(min(zip(r.values(), r.keys()))) |
输出结果: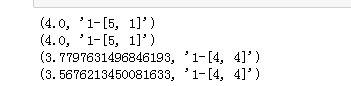
2、实现K近邻树算法
python实现,遍历所有数据点,找出n个距离最近的点的分类情况,少数服从多数
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
|
#k阶近邻算法(少数服从多数)import numpy as npimport pandas as pdimport matplotlib.pyplot as plt%matplotlib inlinefrom sklearn.datasets import load_irisfrom sklearn.model_selection import train_test_splitfrom collections import Counter#1. 载入数据iris = load_iris()df = pd.DataFrame(iris.data, columns=iris.feature_names)df['label'] = iris.targetdf.columns = ['sepal length', 'sepal width', 'petal length', 'petal width', 'label']# data = np.array(df.iloc[:100, [0, 1, -1]])plt.scatter(df[:50]['sepal length'], df[:50]['sepal width'], label='0')plt.scatter(df[50:100]['sepal length'], df[50:100]['sepal width'], label='1')plt.xlabel('sepal length')plt.ylabel('sepal width')plt.legend() |
输出: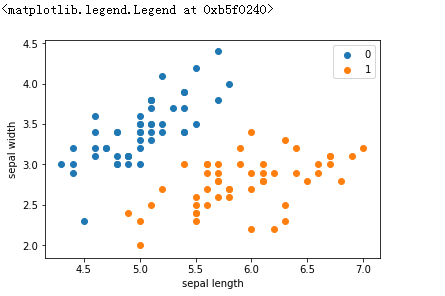
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
|
#2. 构造模型class KNN: def __init__(self, X_train, y_train, n_neighbors = 3, p = 2): self.n = n_neighbors self.p = p self.X_train = X_train self.y_train = y_train def predict(self,X): knn_list = [] for i in range(self.n): dist = np.linalg.norm(X-self.X_train[i],ord=self.p) knn_list.append((dist,self.y_train[i])) for i in range(self.n,len(self.X_train)): max_index = knn_list.index(max(knn_list,key=lambda x : x[0])) dist = np.linalg.norm(X-self.X_train[i],ord=self.p) if knn_list[max_index][0] > dist: knn_list[max_index] = (dist,self.y_train[i]) knn = [k[-1] for k in knn_list] count_pairs = Counter(knn) return count_pairs.most_common(1)[0][0] def score(self, X_test, y_test): right_count = 0 n = 10 for X, y in zip(X_test, y_test): label = self.predict(X) if label == y: right_count += 1 return right_count / len(X_test) |
|
1
|
clf = KNN(X_train, y_train) |
|
1
|
clf.score(X_test, y_test) |
输出:
|
1
2
|
test_point = [6.0, 3.0]print('Test Point: {}'.format(clf.predict(test_point))) |
输出:
|
1
2
3
4
5
6
|
plt.scatter(df[:50]['sepal length'], df[:50]['sepal width'], label='0')plt.scatter(df[50:100]['sepal length'], df[50:100]['sepal width'], label='1')plt.plot(test_point[0], test_point[1], 'bo', label='test_point')plt.xlabel('sepal length')plt.ylabel('sepal width')plt.legend() |
输出:
3、针对iris数据集,应用sklearn的K近邻算法进行类别预测
scikit - learn
sklearn.neighbors.KNeighborsClassifier
n_neighbors: 临近点个数
p: 距离度量
algorithm: 近邻算法,可选{‘auto’, ‘ball_tree’, ‘kd_tree’, ‘brute’}
weights: 确定近邻的权重
|
1
2
3
|
from sklearn.neighbors import KNeighborsClassifierclf_sk = KNeighborsClassifier()clf_sk.fit(X_train, y_train) |
输出:
|
1
|
clf_sk.score(X_test, y_test) |
输出:
4、针对iris数据集,编制程序使用K近邻树进行类别预测
(1)构造kd树
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
|
# kd-tree 每个结点中主要包含的数据如下:class KdNode(object): def __init__(self, dom_elt, split, left, right): self.dom_elt = dom_elt#结点的父结点 self.split = split#划分结点 self.left = left#做结点 self.right = right#右结点class KdTree(object): def __init__(self, data): k = len(data[0])#数据维度 #print("创建结点") #print("开始执行创建结点函数!!!") def CreateNode(split, data_set): #print(split,data_set) if not data_set:#数据集为空 return None #print("进入函数!!!") data_set.sort(key=lambda x:x[split])#开始找切分平面的维度 #print("data_set:",data_set) split_pos = len(data_set)//2 #取得中位数点的坐标位置(求整) median = data_set[split_pos] split_next = (split+1) % k #(取余数)取得下一个节点的分离维数 return KdNode( median, split, CreateNode(split_next, data_set[:split_pos]),#创建左结点 CreateNode(split_next, data_set[split_pos+1:]))#创建右结点 #print("结束创建结点函数!!!") self.root = CreateNode(0, data)#创建根结点 #KDTree的前序遍历def preorder(root): print(root.dom_elt) if root.left: preorder(root.left) if root.right: preorder(root.right) |
(2)搜索kd树
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
|
#KDTree的前序遍历def preorder(root): print(root.dom_elt) if root.left: preorder(root.left) if root.right: preorder(root.right) from math import sqrtfrom collections import namedtuple# 定义一个namedtuple,分别存放最近坐标点、最近距离和访问过的节点数result = namedtuple("Result_tuple", "nearest_point nearest_dist nodes_visited")#搜索开始def find_nearest(tree, point): k = len(point)#数据维度 def travel(kd_node, target, max_dist): if kd_node is None: return result([0]*k, float("inf"), 0)#表示数据的无 nodes_visited = 1 s = kd_node.split #数据维度分隔 pivot = kd_node.dom_elt #切分根节点 if target[s] <= pivot[s]: nearer_node = kd_node.left #下一个左结点为树根结点 further_node = kd_node.right #记录右节点 else: #右面更近 nearer_node = kd_node.right further_node = kd_node.left temp1 = travel(nearer_node, target, max_dist) nearest = temp1.nearest_point# 得到叶子结点,此时为nearest dist = temp1.nearest_dist #update distance nodes_visited += temp1.nodes_visited print("nodes_visited:", nodes_visited) if dist < max_dist: max_dist = dist temp_dist = abs(pivot[s]-target[s])#计算球体与分隔超平面的距离 if max_dist < temp_dist: return result(nearest, dist, nodes_visited) # ------- #计算分隔点的欧式距离 temp_dist = sqrt(sum((p1-p2)**2 for p1, p2 in zip(pivot, target)))#计算目标点到邻近节点的Distance if temp_dist < dist: nearest = pivot #更新最近点 dist = temp_dist #更新最近距离 max_dist = dist #更新超球体的半径 print("输出数据:" , nearest, dist, max_dist) # 检查另一个子结点对应的区域是否有更近的点 temp2 = travel(further_node, target, max_dist) nodes_visited += temp2.nodes_visited if temp2.nearest_dist < dist: # 如果另一个子结点内存在更近距离 nearest = temp2.nearest_point # 更新最近点 dist = temp2.nearest_dist # 更新最近距离 return result(nearest, dist, nodes_visited) return travel(tree.root, point, float("inf")) # 从根节点开始递归 |
(3)例3.2
|
1
2
3
|
data= [[2,3],[5,4],[9,6],[4,7],[8,1],[7,2]]kd=KdTree(data)preorder(kd.root) |
输出: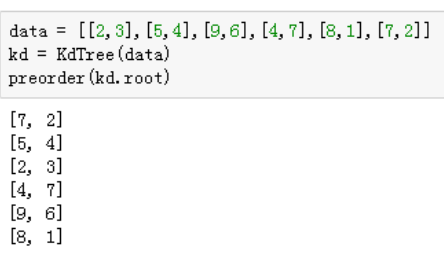
|
1
2
3
4
5
6
7
8
9
10
11
12
|
from time import clockfrom random import random# 产生一个k维随机向量,每维分量值在0~1之间def random_point(k): return [random()for_inrange(k)]# 产生n个k维随机向量def random_points(k, n): return [random_point(k) for_inrange(n)] ret=find_nearest(kd, [3,4.5])print (ret) |
输出:
|
1
2
3
4
5
6
|
N=400000t0=clock()kd2=KdTree(random_points(3, N)) # 构建包含四十万个3维空间样本点的kd树ret2=find_nearest(kd2, [0.1,0.5,0.8]) # 四十万个样本点中寻找离目标最近的点t1=clock()print ("time: ",t1-t0, "s")print (ret2) |
输出:
五、实验小结
- 理解了K-近邻算法原理,能实现算法K近邻算法;
- 掌握了常见的距离度量方法;
- 掌握了K近邻树实现算法;
- 学会了针对特定应用场景及数据,能应用K近邻解决实际问题。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号