有一个概率密度函数p(x),求解随机变量x基于此概率下某个函数f(x)的期望,表示如下:
![]()
如果概率分布形式比较简单的话,我们可以采用解析的方法:
![]()
如果f(x)过于复杂的话,直接求解就非常复杂,我们采用蒙特卡洛的方法。根据大数定理,当采样数量足够大的话,采样样本可以无限近似地表示原分布,我们可以得到:
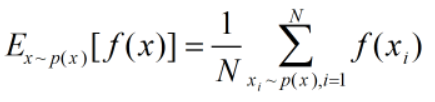
我们令待采样的分布为p(x),另一个简单可采样且定义域与p(x)相同的概率密度函数为![]() :
:

我们只需要简单地从分布![]() 中采样到x,然后分别计算样本在两个分布中的概率和函数值。
中采样到x,然后分别计算样本在两个分布中的概率和函数值。
下面我们进行试验,我们假设要采样的数据来自均值为1,标准差为1的高斯分布,希望用另一个高斯分布来近似这个分布。我们选取三个:均值为1,标准差分别为1、0.5、2的高斯分布来进行比较。为了更好地看出重要性采样的效果,这里的函数将选择一个比较简单的形式f(x)=x:
import numpy as np import math import matplotlib.pyplot as plt def gaussian(x,u,sigma): """ param x:要计算概率密度值的点 param u:均值 param sigma:方差 return x的概率密度值 """ return math.exp(-(x-u)**2/(2*sigma*sigma))/math.sqrt(2*math.pi*sigma*sigma) def importance_sampling_test(ori_sigma,sample_sigma): """ param ori_sigma:原始分布p(x)的方差 param sample_sigma:采样分布p~(x)的方差 return """ origin = [] for n in range(10): #进行10次计算 Sum = 0 for i in range(100000): a = np.random.normal(1.0,ori_sigma) Sum += a origin.append(Sum) isample = [] for n in range(10): Sum2 = 0 for i in range(100000): a = np.random.normal(1.0,sample_sigma) #计算从正太分布采样出来的x ua = gaussian(a,1.0,sample_sigma) #计算采样概率密度 na = gaussian(a,1.0,ori_sigma) #计算原始概率密度 Sum2 += a*na/ua isample.append(Sum2) origin = np.array(origin) isample = np.array(isample) print(np.mean(origin),np.std(origin)) print(np.mean(isample),np.std(isample)) importance_sampling_test(1.0,1.0) importance_sampling_test(1.0,0.5) importance_sampling_test(1.0,2.0) xs = np.linspace(-5,6,301) y1 = [gaussian(x,1.0,1.0) for x in xs] y2 = [gaussian(x,1.0,0.5) for x in xs] y3 = [gaussian(x,1.0,2.0) for x in xs] fig = plt.figure(figsize=(8,5)) plt.plot(xs,y1,label="sigma=1.0") plt.plot(xs,y2,label="sigma=0.5") plt.plot(xs,y3,label="sigma=2.0") plt.legend() plt.show()



 浙公网安备 33010602011771号
浙公网安备 33010602011771号