数组

数组定义

如果说现在要求你定义100个整型变量，那么如果按照之前的做法，可能现在定义的的结构如下：

int i1,i2,...i100;

但是这个时候如果按照此类方式定义就会非常麻烦，因为这些变量彼此之间没有任何的关联，也就是说如果现在突然再有一个要求，要求你输出这100个变量的内容，意味着你要编写System.out.println()语句100次。

其实所谓的数组指的就是一组相关类型的变量集合，并且这些变量可以按照统一的方式进行操作。数组本身属于引用数据类型，那么既然是引用数据类型，这里面实际又会牵扯到内存分配，而数组的定义语法有如下。

int[] nums = new int[10];//动态初始化

int[] nums2 = {1,2,3,4};//静态初始化

数组使用注意事项

数组下标是从0开始到数组长度-1为止，不能使用超出这个范围的下标索引，否则会出现数组下标越界的异常
数组一旦初始化确定其容量之后，数组的容量就无法改变
数组属于引用类型，我们在定义数组之后，即使没有进行赋值，数组里面也会有相应的默认值，int类型为0，double类型为0.0，char类型为\u0000,boolean类型为false，引用类型为null。

数组在没有初始化的时候不能直接使用，会出现空指针异常，例如下面代码：

int[] nums;
System.out.println(nums.length);//会出现空指针异常，必须先初始化再使用

数组的内存结构

我们通过一段代码来分析数组在内存中的结构，在Java中我们可以将内存大致分为三块区域，堆、栈、方法区。栈主要用来存储一些局部变量，每调用一个方法都会在栈中开辟一块空间，最底层是main开辟的空间。堆主要用来存储一些实例对象，每new创建一个对象都会在堆中开辟对象空间。方法区，目前我们可以理解存储一些常量，也就是常量池。我们先看下面这段代码：

int[] nums = new int[4];
nums[0] = 1;
nums[1] = 2;
nums[2] = 3;
nums[3] = 4;
System.out.println(Arrays.toString(nums));

当程序执行第一行代码的时候，会在栈中定义一个int[]变量nums,然后在堆中开辟一个int[4]大小的空间，并将其地址返回给nums变量，这时候并没有给数组里面的值赋值，不过里面每个位置有默认值0。

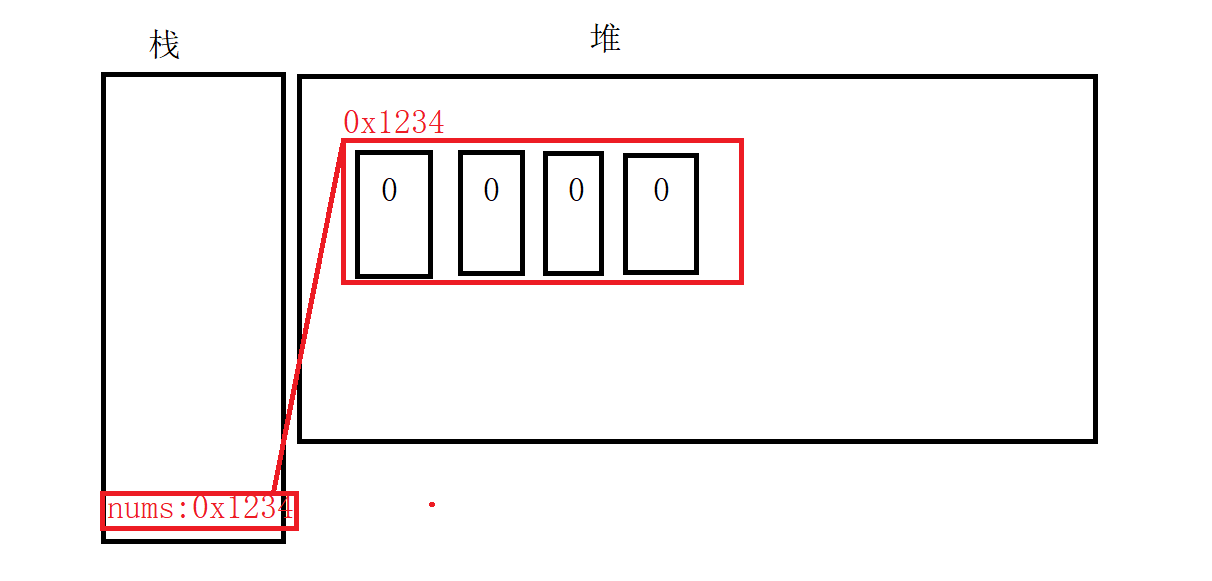
然后执行2-5句代码，对数组中的值依次赋值：

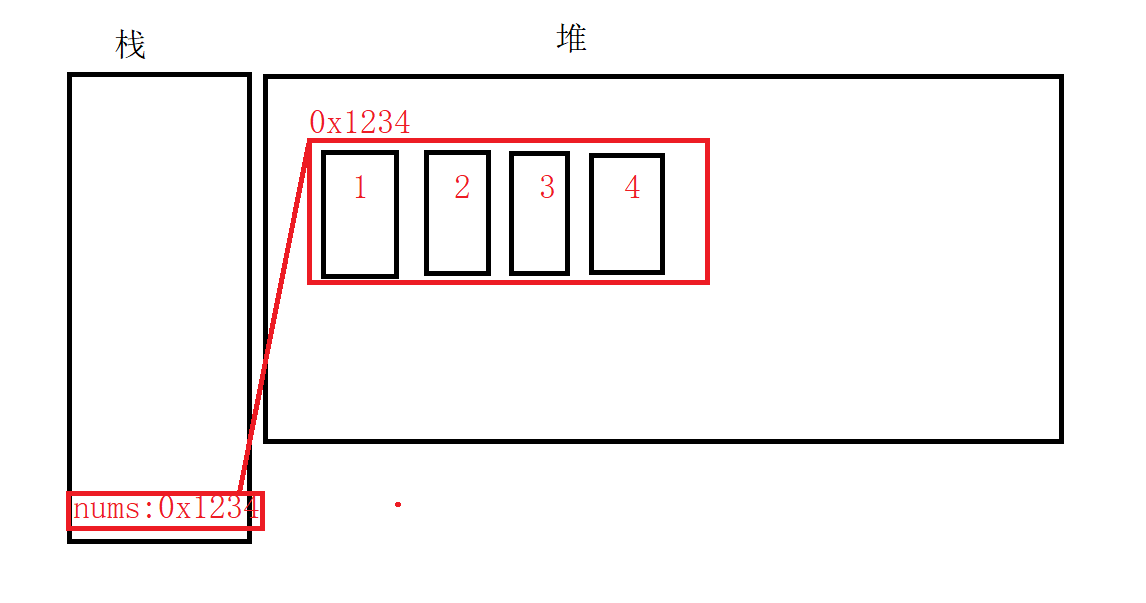
最后调用输出语句，对数组中的值依次输出。

数组的使用

使用forEach循环遍历数组

//我们传统遍历数组的方法如下：
int[] nums = {1,2,3,4,5,6,7};
        
for(int i = 0; i < nums.length; i++){
    System.out.println(nums[i]);
}

//使用foreach遍历数组的时候我们不用关心索引下标越界
for (int num : nums) {
    System.out.println(num);
}

作为方法参数传入

//打印数组内容
public static void printArray(int[] arr){
    for (int i : arr) {
        System.out.print(i + " ");
    }
    System.out.println();
}

作为返回值返回

//反转数组内容
public static int[] reversalArray(int[] arr){
    int[] result = new int[arr.length];
    for(int i = 0, j = arr.length-1; i < result.length; i++,j--){
        result[i] = arr[j];
    }

    return result;
}

多维数组

多维数组最简单的理解就是数组里面再嵌套数组，数组里面每一个元素又是一个数组，这就形成了Java里面多维数组的概念。实例代码：

//定义并给多维数组赋值
int[][] nums = {{1,2},{3,4},{5,6}};
//输出多维数组
for(int i = 0; i < nums.length; i++){
    for(int j = 0; j < nums[i].length; j++){
        System.out.print(nums[i][j] + "\t");
    }
    System.out.println();
}
/*
结果：
1	2	
3	4	
5	6	
*/

Arrays类工具类

Arrays 类是一个工具类，其中包含了数组操作的很多方法。这个 Arrays 类里均为 static 修饰的方法（static 修饰的方法可以直接通过类名调用），可以直接通过 Arrays.xxx(xxx) 的形式调用方法。

我们这里只讲解比较常用的几个方法对其底层原理进行分析，如果遇到不懂的方法可以自行查看JavaAPI文档。

fill方法
用指定数填充数组，第一个参数为要填充的数组，第二个为要填充的值。实例演示：

int[] num2 = new int[5];
Arrays.fill(num2,5);
System.out.println(Arrays.toString(num2));

底层源码：

public static void fill(int[] a, int val) {
    for (int i = 0, len = a.length; i < len; i++)
        a[i] = val;
}

用一个for循环给数组每一个位置赋值。

sort方法

该方法对给定数组的数组元素进行排序，参数为要进行排序的数组，实例演示：

int[] num1 = {8,5,9,7,13,2,4,1};
System.out.println("原数组:" + Arrays.toString(num1));
Arrays.sort(num1);
System.out.println("排序之后的数组: " + Arrays.toString(num1));
/*
结果
原数组:[8, 5, 9, 7, 13, 2, 4, 1]
排序之后的数组: [1, 2, 4, 5, 7, 8, 9, 13]
*/

底层源码:

//这里仅仅分析我们这段代码执行的底层逻辑，数组不一样，底层执行的代码也可能不一样
public static void sort(int[] a) {
    DualPivotQuicksort.sort(a, 0, a.length - 1, null, 0, 0);
}


static void sort(int[] a, int left, int right,
                     int[] work, int workBase, int workLen) {
    // Use Quicksort on small arrays QUICKSORT_THRESHOLD =286
    if (right - left < QUICKSORT_THRESHOLD) {
        sort(a, left, right, true);
        return;
    }
    ...
}


private static void sort(int[] a, int left, int right, boolean leftmost) {
        int length = right - left + 1;
    	// Use insertion sort on tiny arrays INSERTION_SORT_THRESHOLD=47
        if (length < INSERTION_SORT_THRESHOLD) {
            if (leftmost) {//leftmost=true
                /*
                 * 传统插入排序，最核心部分，每次遍历，确定当前位置和之前所有元素的大小顺序
                 */
                for (int i = left, j = i; i < right; j = ++i) {
                    int ai = a[i + 1];
                    while (ai < a[j]) {
                        a[j + 1] = a[j];
                        if (j-- == left) {
                            break;
                        }
                    }
                    a[j + 1] = ai;
                }
            }else{
                ...
            }
            return;
        }
        ...
      }
      ...
}

binarySearch方法

使用二分法查询 key 元素值在 a 数组中出现的索引，如果 a 数组不包含 key 元素值，则返回负数。调用该方法时要求数组中元素己经按升序排列，这样才能得到正确结果。

int[] num1 = {8,5,9,7,13,2,4,1};
System.out.println("原数组:" + Arrays.toString(num1));
Arrays.sort(num1);
System.out.println("排序之后的数组: " + Arrays.toString(num1));
int index = Arrays.binarySearch(num1,5);
System.out.println(index);

/*
原数组:[8, 5, 9, 7, 13, 2, 4, 1]
排序之后的数组: [1, 2, 4, 5, 7, 8, 9, 13]
3
*/

底层源码

public static int binarySearch(int[] a, int key) {
    return binarySearch0(a, 0, a.length, key);
}


// Like public version, but without range checks.
private static int binarySearch0(int[] a, int fromIndex, int toIndex,
                                 int key) {
    int low = fromIndex;
    int high = toIndex - 1;

    while (low <= high) {
        int mid = (low + high) >>> 1;
        int midVal = a[mid];

        if (midVal < key)
            low = mid + 1;
        else if (midVal > key)
            high = mid - 1;
        else
            return mid; // key found
    }
    return -(low + 1);  // key not found.
}

通过一个循环，先通过首位索引确定数组的中间位置的索引，判断我们要找的值是否是该值，或者比该值小，或者大。当比中间位置元素小的时候，就可以确定要找的元素在数组上半区，此时可以再对上半区元素再一分为二进行判断，直到找到那个元素为止。

冒泡排序

冒泡排序（Bubble Sort）也是一种简单直观的排序算法。它重复地走访过要排序的数列，一次比较两个元素，如果他们的顺序错误就把他们交换过来。走访数列的工作是重复地进行直到没有再需要交换，也就是说该数列已经排序完成。这个算法的名字由来是因为越小的元素会经由交换慢慢"浮"到数列的顶端。

作为最简单的排序算法之一，冒泡排序给我的感觉就像 Abandon 在单词书里出现的感觉一样，每次都在第一页第一位，所以最熟悉。冒泡排序还有一种优化算法，就是立一个 flag，当在一趟序列遍历中元素没有发生交换，则证明该序列已经有序。但这种改进对于提升性能来说并没有什么太大作用。

1. 算法步骤

比较相邻的元素。如果第一个比第二个大，就交换他们两个。

对每一对相邻元素作同样的工作，从开始第一对到结尾的最后一对。这步做完后，最后的元素会是最大的数。

针对所有的元素重复以上的步骤，除了最后一个。

持续每次对越来越少的元素重复上面的步骤，直到没有任何一对数字需要比较。

2.动画演示

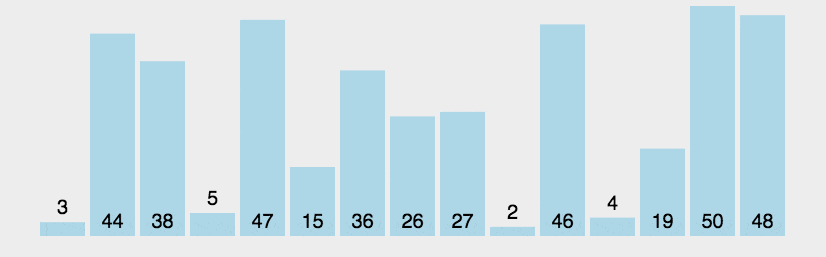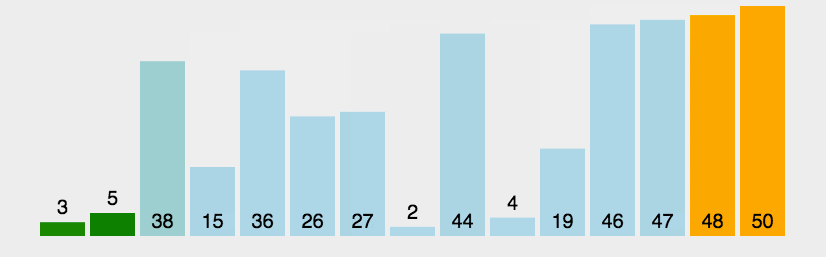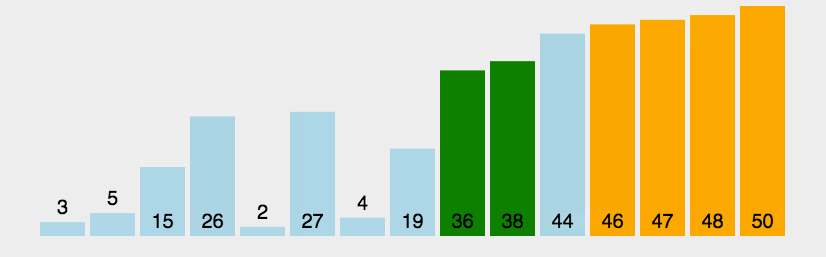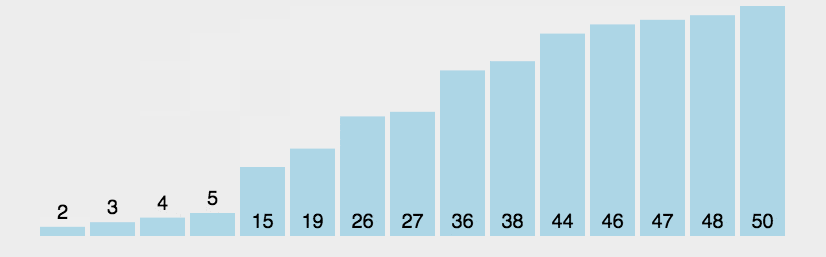
3. 什么时候最快

当输入的数据已经是正序时（都已经是正序了，我还要你冒泡排序有何用啊）。

4. 什么时候最慢

当输入的数据是反序时（写一个 for 循环反序输出数据不就行了，干嘛要用你冒泡排序呢，我是闲的吗）。

5.代码实现

int[] nums = {8,5,9,7,13,2,4,1};

System.out.println("排序之前: " + Arrays.toString(nums));
//冒泡排序
for(int i = 1; i < nums.length; i++){
    for(int j = 0; j < nums.length - i; j++){
        if(nums[j] > nums[j+1]){
            int temp = nums[j];
            nums[j] = nums[j+1];
            nums[j+1] = temp;
        }
    }
}
System.out.println("排序之后: " + Arrays.toString(nums));
/*
排序之前: [8, 5, 9, 7, 13, 2, 4, 1]
排序之后: [1, 2, 4, 5, 7, 8, 9, 13]
*/

//优化，添加一个标志位，如果没有进行交换元素，说明数组已经是顺序，就可以直接结束循环
//冒泡排序
for(int i = 1; i < nums.length; i++){ 
    boolean flag = true;
    for(int j = 0; j < nums.length - i; j++){
        if(nums[j] > nums[j+1]){
            int temp = nums[j];
            nums[j] = nums[j+1];
            nums[j+1] = temp;
            flag = false;
        }
    }

    if(flag){
        break;//没有进行交换元素，说明数组已经是顺序，直接结束循环
    }
}

冒泡排序的时间复杂度是O(n^2)

稀疏数组

所谓稀疏数组，从字面上我们也可以得知，它仍然是一个数组，他的作用就是将一个对应的数组数据进行优化，比如，我们将上面的二维数组进行优化。可以节约内存空间。我们来做一个实际的演示，对稀疏数组的转化和应用来进行说明

背景

如下图所示，这里有一个 15 × 15 的棋盘，如果现在要让你通过编码的方式，让你将这盘棋局保存起来，你会怎么做呢？

面对行列数据的保存，我相信大多人第一时间都会想到用二维数组进行保存。
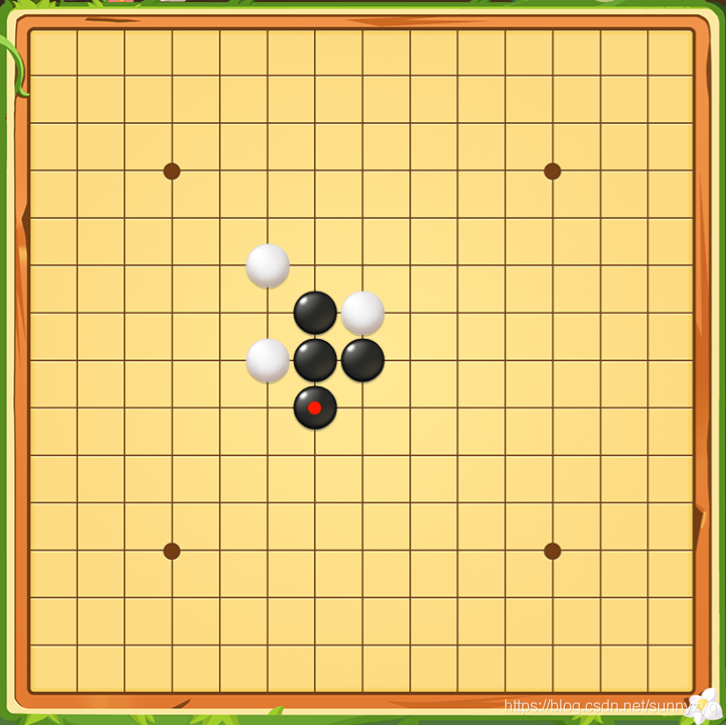
普通数组保存棋盘数据

比如，我们可以将棋盘进行抽象化，用一个 15 × 15 的二维数组来表示，然后用 0 表示空点，用 1 表示白子，用 2 表示黑子，于是就可以抽象为如下模样。

int[][] arr = new int[15][15];
//保存白棋
arr[5][5] = 1;
arr[7][5] = 1;
arr[6][7] = 1;

//保存黑棋
arr[6][6] = 2;
arr[7][6] = 2;
arr[8][6] = 2;
arr[7][7] = 2;

//输出棋盘数据
for(int i = 0; i < arr.length; i++){
    for(int j = 0; j < arr[i].length; j++){
        System.out.print(arr[i][j] + " ");
    }
    System.out.println();
}

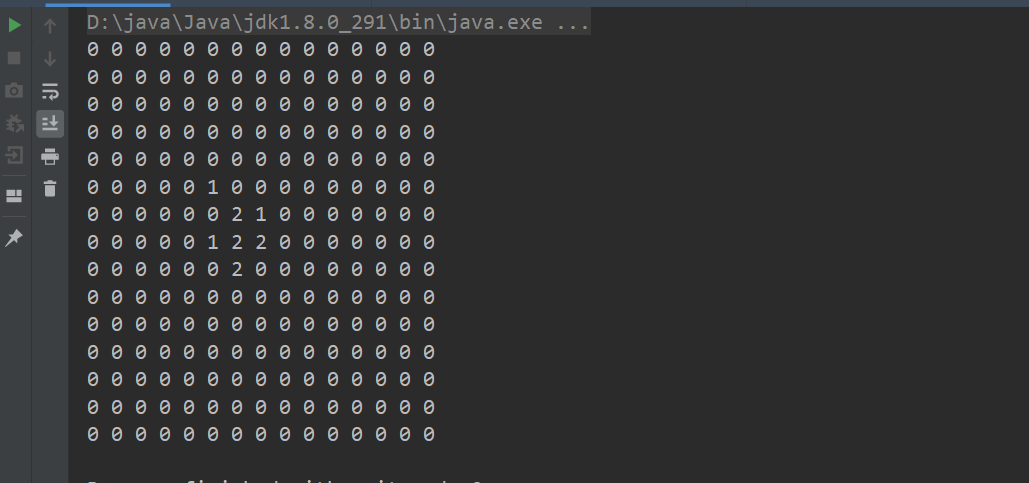
普通数组的不足之处

上面，我们通过了一个最普通的方法，将棋盘数据保存在了一个二维数组中，整个数组我们用了 15 × 15（共 225）个点来保存数据，其中有 218 个点都是空的。实际来说，我们只需要将有价值的黑白子保存起来即可，因为只要我们知道黑白子数据，以及棋盘的大小，那么这 218 个空点是可以不用进行保存的。把这样没有价值的数据起来，不但会浪费存储空间的大小，如果写入到磁盘中，还会增大 IO 的读写量，影响性能，这就是用普通二维数组来表示棋盘数据的不足之处。总结使用普通数组保存棋盘数据太浪费空间

稀疏数组保存数据

这个棋盘的关键数据很少，我们只需要记录下，棋盘的行列，所有白棋的坐标，所有黑棋的坐标即可。

行	列	值
15	15	7
5	5	1
7	5	1
6	7	1
6	6	2
7	6	2
8	6	2
7	7	2

我们只需要创建一个8行3列的数组即可，这样保存的每一个数据都是有价值的，节省空间。

//将普通数组转换为稀疏数组
int valueSize = 0;//用于记录原数组中不为零值的个数
for(int i = 0; i < arr.length; i++){
    for(int j = 0; j < arr[i].length; j++) {
        if(arr[i][j] != 0){
            valueSize++;
        }
    }
}
//创建稀疏数组,多一行用于记录原数组的行列，不为零的个数
int[][] arr1 = new int[valueSize+1][3];
//设置原数组的行列不为零的个数
arr1[0][0] = 15;
arr1[0][1] = 15;
arr1[0][1] = valueSize;
System.out.println("个数：" + valueSize);
//遍历原数组，将不为零的值坐标和值记录下来
int countValue = 1;//用于记录每个不为零的值在稀疏数组中的行号
for(int i = 0; i < arr.length; i++){
    for(int j = 0; j < arr[i].length; j++) {
        if(arr[i][j] != 0){
            arr1[countValue][0] = i;
            arr1[countValue][1] = j;
            arr1[countValue][2] = arr[i][j];
            countValue++;
        }
    }
}
//输出稀疏数组
System.out.println("转换之后的稀疏数组:");
for(int i = 0; i < arr1.length; i++){
    for(int j = 0; j < arr1[i].length; j++){
        System.out.print(arr1[i][j] + " ");
    }
    System.out.println();
}

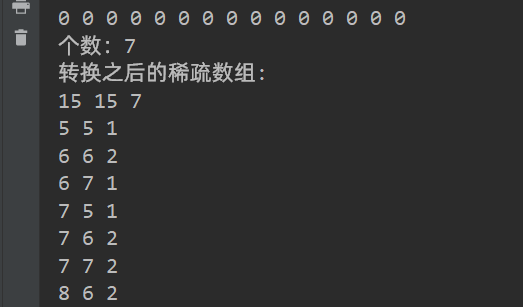
将稀疏数组还原为原数组：

//将稀疏数组还原为原数组
int[][] arr2 = new int[arr1[0][0]][arr1[0][1]];

//将白棋和黑棋数据写入
for(int i = 1; i < arr1[0][2]; i++){
    arr2[arr1[i][0]][arr1[i][1]] = arr1[i][2];
}
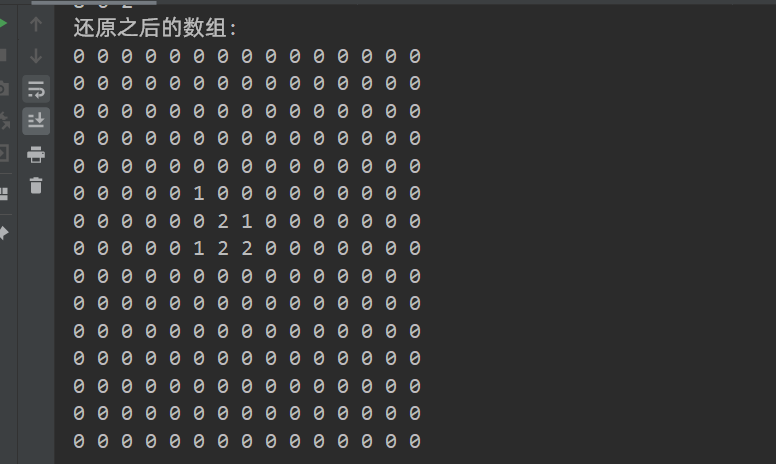
System.out.println("还原之后的数组:");
//输出原数组
for(int i = 0; i < arr2.length; i++){
    for(int j = 0; j < arr2[i].length; j++){
        System.out.print(arr2[i][j] + " ");
    }
    System.out.println();
}

posted @ 2021-09-21 10:57 无涯子wyz 阅读(78) 评论(0) 收藏举报

刷新页面返回顶部

无涯子

数组