第一次作业：深度学习基础

1. 视频学习

1.1 绪论

什么是人工智能
使一部机器像人一样进行感知、认知、决策、执行的人工程序或系统。
图灵测试
人机测试，判断是人还是机器在操作。
机器学习

基于数据自动学习

减少人工复杂工作，但结果可能不易解释

提高信息处理的效率，且准确率较高

来源于真实数据，减少人工规则主观性，可信度高模型分类

模型分类

数据标记

监督学习模型：输入样本具有标记，从数据中学习标记分界面，适用于预测数据标记
无监督学习模型：输入样本没有标记，从数据中学习模式，适用于描述数据
半监督学习：部分数据标记已知
强化学习：数据标记未知，但知道与输出目标相关的反馈

数据分布

参数模型：对数据分布进行假设，待求解的数据模式/映射可以用一组有限且固定数目的参数进行刻画
非参数模型：不对数据分布进行假设，数据的所有统计特征都来源于数据本身

建模对象

生成模型：对输入和输出的联合分布P(X,Y)建模；从数据中先学习到X和Y的联合分布，然后通过贝叶斯公式求的P(Y|X)
判别模型：对已知输入X条件下输出Y的条件分布P(Y|X)建模；直接学习P(Y|X)，输入X，直接预测Y

1.2 深度学习概述

M-P神经元

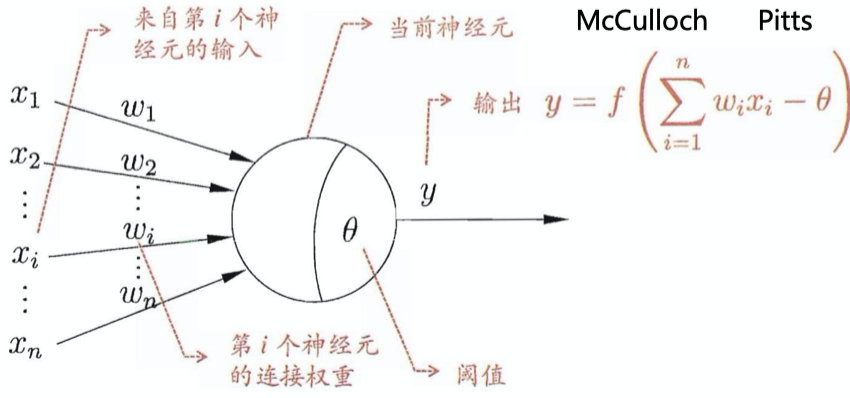
激活函数

输入超过阈值，神经元被激活，但不一定传递

没有激活函数相当于矩阵相乘；每一层相当于一个矩阵，矩阵相乘仍为矩阵，即多层和一层一样

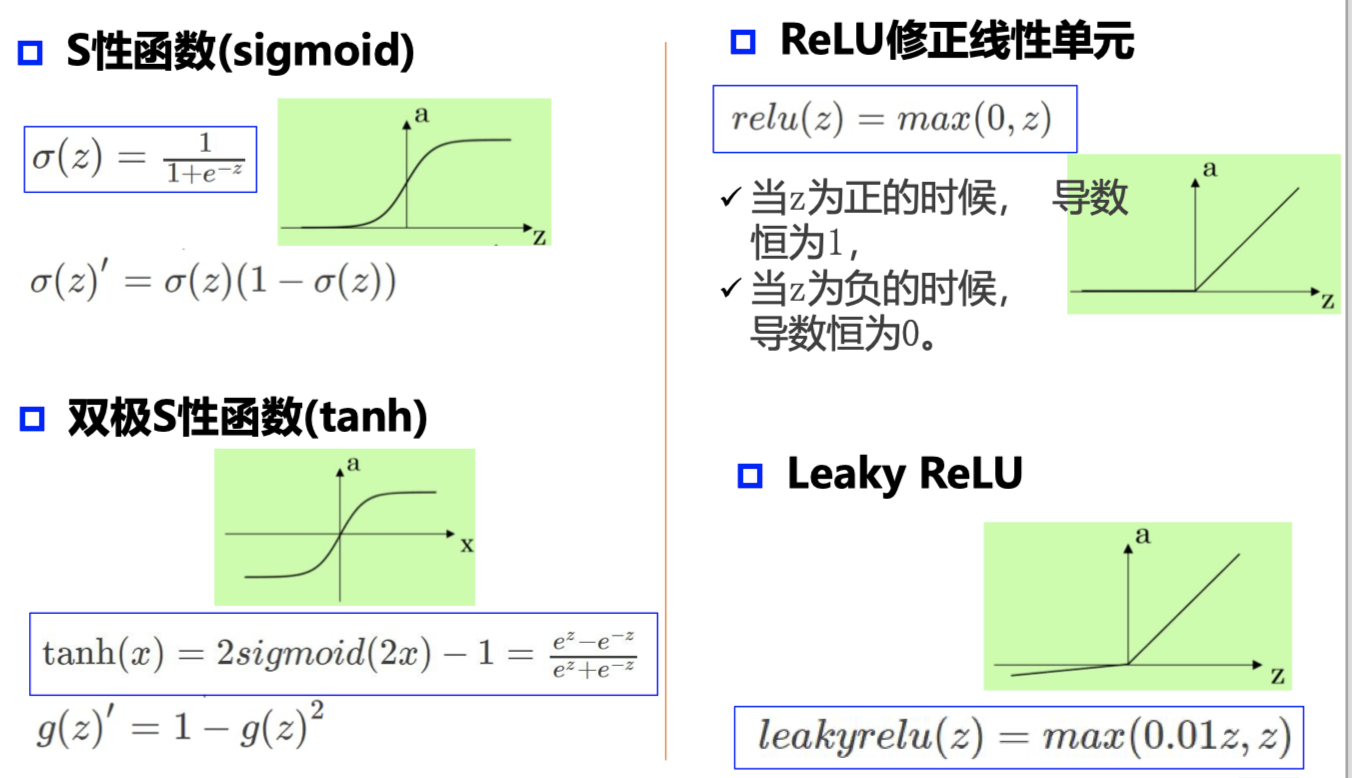
梯度和梯度下降

参数沿负梯度方向更新可以使函数值下降，但可能会陷入局部极值点，无法找到全局的极值点（与初始点位置有关）

深度学习使用两个优化器：Adam 和 SGD 一般来说，使用 Adam 就可以，效果会比较好

自编码器(autoencoder)

假设输出与输入相同(target=input)，是一种尽可能复现输入信号的神经网络.将input输入一个encoder编码器，就会得到一个code；加一个decoder解码器，输出信息。

通过调整encoder和decoder的参数，使得重构误差最小

没有额外监督信息: 无标签数据，误差的来源是直接重构后信号与原输入相比得到

解决梯度消失

1.3 pytorch 基础

结合2.2进行练习

2 代码练习

2.1 Python中的图像处理

2.1.1 下载并显示图像

plt.subplot(121) #1代表行，2代表列，所以一共有2个图，1代表此时绘制第二个图。
plt.imshow(colony[:,:,:])
plt.title('3-channel image')
plt.axis('off') #不显示坐标尺寸

2.1.2 读取并改变图像像素值

# Get the pixel value at row 10, column 10 on the 10th row and 20th column
camera = data.camera()#灰度“camera”图像。通常用于分割和去噪示例。
print(camera[10, 20]) 

# Set a region to black
camera[30:100, 10:100] = 0
plt.imshow(camera, 'gray')

# Set the first ten lines to black
camera = data.camera()
camera[:10] = 0
plt.imshow(camera, 'gray')

# Set to "white" (255) pixels where mask is True
camera = data.camera()
mask = camera < 80 #mask是一个bool数组512 x 512，像素值大于80的位置上mask数组的值为False，其余为True。
camera[mask] = 255
plt.imshow(camera, 'gray')

# Change the color for real images
cat = data.chelsea() #以纹理为例，水平和对角方向上的突出边缘以及不同比例的特征。
plt.imshow(cat)

# Set brighter pixels to red
red_cat = cat.copy()
reddish = cat[:, :, 0] > 160# 红色的值大于160（0red 1green 2blue）
red_cat[reddish] = [255, 0, 0]#设为红色
plt.imshow(red_cat)

# Change RGB color to BGR for openCV
BGR_cat = cat[:, :, ::-1] #实现RGB到BGR通道的转换 （若图片一开始就是BGR的，就是实现从BGR到RGB的转换）。
plt.imshow(BGR_cat)

2.1.3 转换图像数据类型

img_as_float Convert to 64-bit floating point.
img_as_ubyte Convert to 8-bit uint.
img_as_uint Convert to 16-bit uint.
img_as_int Convert to 16-bit int.

2.1.4 显示图像直方图

plt.hist(img.ravel(), bins=256, histtype='step', color='black');

matplot.pyplot.hist(x, bins=None, range=None, density=None, weights=None, cumulative=False, bottom=None, histtype='bar', align='mid', orientation='vertical', rwidth=None, log=False, color=None, label=None, stacked=False, normed=None, *, data=None, **kwargs)

x : (n,) array or sequence of (n,) arrays

这个参数是指定每个bin(箱子)分布的数据,对应x轴

bins : integer or array_like, optional

这个参数指定bin(箱子)的个数,也就是总共有几条条状图

normed : boolean, optional

If True, the first element of the return tuple will be the counts normalized to form a probability density, i.e.,n/(len(x)`dbin)

这个参数指定密度,也就是每个条状图的占比例比,默认为1

color : color or array_like of colors or None, optional

这个指定条状图的颜色

2.1.5 图像分割

图像阈值分割是一种广泛应用的分割技术，利用图像中要提取的目标区域与其背景在灰度特性上的差异，把图像看作具有不同灰度级的两类区域(目标区域和背景区域)的组合，选取一个比较合理的阈值，以确定图像中每个像素点应该属于目标区域还是背景区域，从而产生相应的二值图像。

# Use thresholding
plt.imshow(img>0.5)

2.1.6 Canny 算子用于边缘检测

img_edges = canny(img)#？
img_filled = ndi.binary_fill_holes(img_edges)#？

2.1.7 改变图像的对比度

# Contrast stretching
p2, p98 = np.percentile(img, (2, 98))
img_rescale = exposure.rescale_intensity(img, in_range=(p2, p98))#直方图对比度拉伸
plt.imshow(img_rescale, 'gray')

# Equalization
img_eq = exposure.equalize_hist(img) #直方图全局均衡化
plt.imshow(img_eq, 'gray')

# Adaptive Equalization
img_adapteq = exposure.equalize_adapthist(img, clip_limit=0.03)#直方图自适应均衡化
plt.imshow(img_adapteq, 'gray')

2.2 pytorch 基础练习

具体详见：https://pytorch-cn.readthedocs.io/zh/latest/

2.3 螺旋数据分类

考虑逻辑回归的情况。如果将用于分类的逻辑回归用于此数据，它将创建一组线性平面（决策边界），以尝试将数据分为其类。该解决方案的问题在于，在每个区域中，都有属于多个类别的点。螺旋的分支越过线性决策边界，这不是一个很好的解决方案。我们对输入空间进行转换，以使数据被迫线性分离。在训练神经网络来执行此操作的过程中，它学习的决策边界将尝试适应训练数据的分布。

当尝试使用线性决策边界分离螺旋数据时，我们可以达到的最佳精度是50％。

# nn 包用来创建线性模型
# 每一个线性模型都包含 weight 和 bias
model = nn.Sequential(
    nn.Linear(D, H),
    nn.Linear(H, C)
)
model.to(device) # 把模型放到GPU上

# nn 包含多种不同的损失函数，这里使用的是交叉熵（cross entropy loss）损失函数
criterion = torch.nn.CrossEntropyLoss()

# 这里使用 optim 包进行随机梯度下降(stochastic gradient descent)优化
optimizer = torch.optim.SGD(model.parameters(), lr=learning_rate, weight_decay=lambda_l2)

当ReLU（）激活函数时，精度高达95％。这是因为边界变得非线性并更好地适应数据的螺旋形式。

# 这里可以看到，和上面模型不同的是，在两层之间加入了一个 ReLU 激活函数
model = nn.Sequential(
    nn.Linear(D, H),
    nn.ReLU(),
    nn.Linear(H, C)
)
model.to(device)

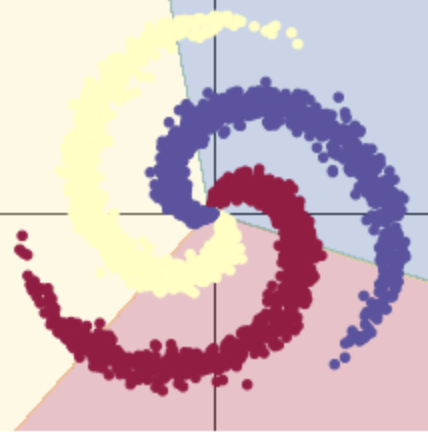
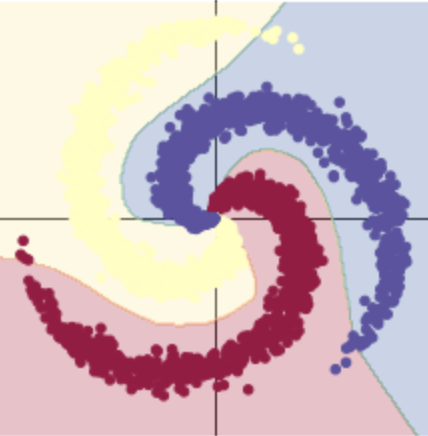
2.4 回归分析

2.4.1 建立线性模型 (两层网络间没有激活函数)

# 建立神经网络模型
model = nn.Sequential(
    nn.Linear(D, H),
    nn.Linear(H, C)
)
model.to(device) # 模型转到 GPU

# 对于回归问题，使用MSE损失函数
criterion = torch.nn.MSELoss()

# 定义优化器，使用SGD
optimizer = torch.optim.SGD(model.parameters(), lr=learning_rate, weight_decay=lambda_l2) # built-in L2

# 开始训练
for t in range(1000):
    # 数据输入模型得到预测结果
    y_pred = model(X)
    # 计算 MSE 损失
    loss = criterion(y_pred, y)
    print("[EPOCH]: %i, [LOSS or MSE]: %.6f" % (t, loss.item()))
    display.clear_output(wait=True)
    # 反向传播前，梯度清零
    optimizer.zero_grad()
    # 反向传播
    loss.backward()
    # 更新参数
    optimizer.step()

2.4.2 两层神经网络

# 这里定义了2个网络，一个 relu_model，一个 tanh_model，
# 使用了不同的激活函数
relu_model = nn.Sequential(
        nn.Linear(D, H),
        nn.ReLU(),
        nn.Linear(H, C)
)
relu_model.to(device)

tanh_model = nn.Sequential(
        nn.Linear(D, H),
        nn.Tanh(),
        nn.Linear(H, C)   
)
tanh_model.to(device)

# MSE损失函数
criterion = torch.nn.MSELoss()
# 定义优化器，使用 Adam，这里仍使用 SGD 优化器的化效果会比较差
optimizer_relumodel = torch.optim.Adam(relu_model.parameters(), lr=learning_rate, weight_decay=lambda_l2) 
optimizer_tanhmodel = torch.optim.Adam(tanh_model.parameters(), lr=learning_rate, weight_decay=lambda_l2)

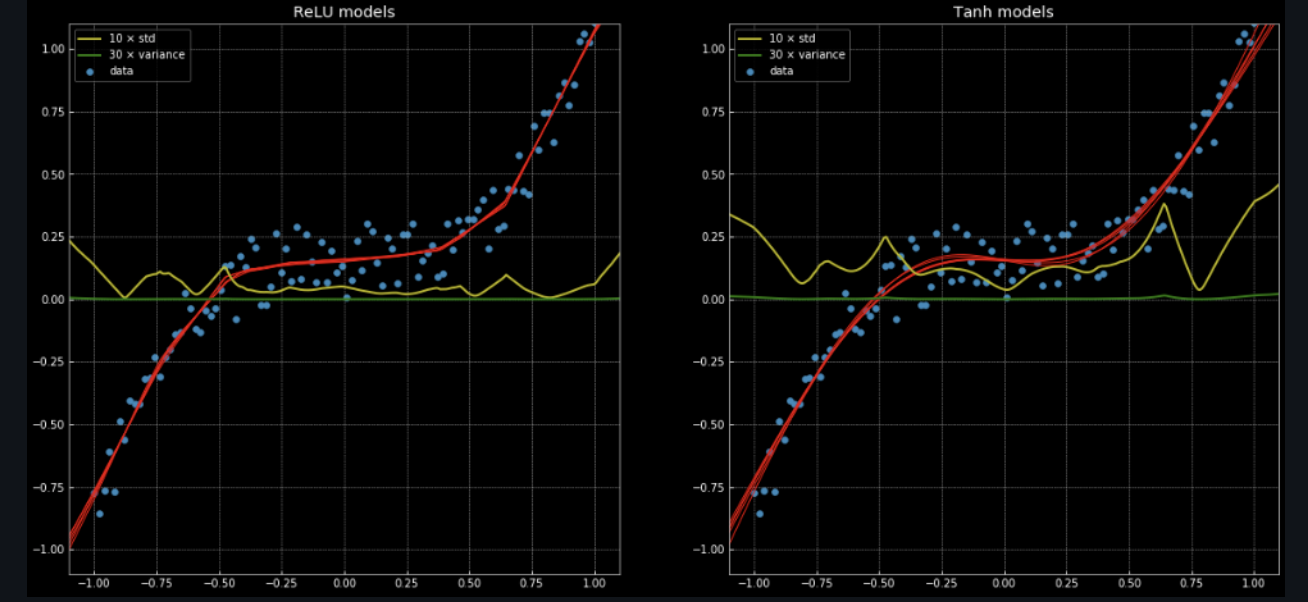
左侧是使用 ReLU 激活函数的网络得到的结果，右侧是使用 Tanh 激活函数的网络得到的结果。前者是分段线性函数，而后者是连续且平滑的回归。
使用 ReLU 激活函数，收敛较快；使用 Tanh 激活函数，一开始收敛较慢，但随后也快速收敛达到较好的效果。 ReLU 激活函数的值是0或1，Tanh 激活函数的值在0～1，前者在两个值之间变动收敛会快。

posted @ 2020-07-25 15:44 Wxxuan 阅读(248) 评论(0) 收藏举报

刷新页面返回顶部

Xuan