自动微分方法(auto diff)
学习机器学习的同学在学习过程中会经常遇到一个问题,那就是对目标函数进行求微分,线性回归这类简单的就不说、复杂的如神经网络类那些求导过程的酸爽。像我还是那种比较粗心的人往往有十导九错,所以说自动求导就十分有必要了,本文主要介绍几种求导的方式。假设我们的函数为\(f(x,y)=x^2y+y+2\),目标是求出偏导\(\frac{\partial{f}}{\partial{x}}\)和\(\frac{\partial{f}}{\partial{y}}\)。求导的方式主要分为以下几种
手动求导法(Manual Differentiation)###
首先准备一张纸和一支笔,根据上学时候学到的求导法则,开始计算。最终得到的结果
\(\frac{\partial{f}}{\partial{x}}=2xy\)
\(\frac{\partial{f}}{\partial{y}}=x^2+1\)
上面这个小例子比较简单,口算即可得到答案,但如果方程比较复杂那就难说了。幸好有自动求导的方法,例如符号求导方法。
符号求解法(Symbolic Differentiation)###
符号求导是根据一些求导法则,进行求导。例如我们大学高数学习的\((uv)\prime=u'v+v'u\),\((u+v)'=u'+v'\),\((\frac{u}{v})'=\frac{u'v-v'u}{v^2}\)等等,下图是\(g(x,y)=5+xy\)的符号求导工作流程。
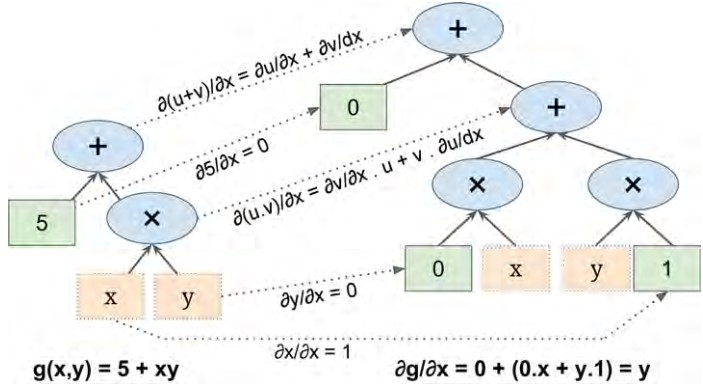
原公式在图的左边,求导公式在图的右半部分,求导的过程是先求叶子节点,自下向上。最终对节点进行见之得到求导结果\(\frac{\partial{g}}{\partial{x}}=y\),这个例子固然简单,但是对于一个更复杂的公式,那么求导符号图将会十分的庞大(表达式膨胀),另外对于一些变化的公式(硬代码)这种方法就无能为力了:
def fun(a,b):
z=0
for i in range(100):
z = a * np.cos(z + i) + z * np.sin(b - i)
return z
数值求导法(Numerical Differentiation)###
导数的定义是当自变量的增量趋于零时,因变量的增量与自变量的增量之商的极限。
其中\(\varepsilon\)是一个无穷小的数,所以我们可以计算在x=3,y=4这一点对x的偏导数,\(f'(x=3,y)=\frac{f(3+\varepsilon,4)-f(3,4)}{\varepsilon}\),对应的代码如下:
def f(x, y):
return x**2*y + y + 2
def derivative(f, x, y, x_eps, y_eps):
return (f(x + x_eps, y + y_eps) - f(x, y)) / (x_eps + y_eps)
df_dx = derivative(f, 3, 4, 0.00001, 0)
df_dy = derivative(f, 3, 4, 0, 0.00001)
>>print(df_dx)
24.000039999805264
>>print(df_dy)
10.000000000331966
通过上面的结果我们发现,得出的结果不是十分的精确,并且在对x和y求偏导的整个过程中,至少需要计算3次\(f()\),也就是说如果有1000个参数,那么至少需要计算1001次\(f()\),在神经网络中,参数巨多,这样计算效率会比较差。不过这种方法常被用到进行检验得到的求导结果是否正确。
前向自动求导法(Forward-Mode Autodiff)###
前向求导是依赖于数值求导和符号求导的一种求解方法,给定公式\(a+{\varepsilon}b\),这种被称作dual number,其中a和b是实数,\(\varepsilon\)是一个无穷小的数,并且\({\varepsilon}^2=0\),举个栗子,\(42 + 24\varepsilon\),我们可以把它看成42.00000000...24的数值.我们可以通过这种方法(42.0,24.0)来表示,dual number满足以下的运算法则:
- 1.\(\lambda(a+b\varepsilon) = a\varepsilon + b{\lambda}\varepsilon\)
- 2.\((a+b\varepsilon)+(c+d\varepsilon) = (a+c)+(b+d)\varepsilon\)
- 3.\((a+b\varepsilon)\times(c+d\varepsilon) = ac+(ad+bc)\varepsilon+(bd){\varepsilon}^2=ac+(ad+bc)\varepsilon\)
还有一点就是\(h(a+b\varepsilon)=h(a)+b{\times}h'(a)\varepsilon\)。
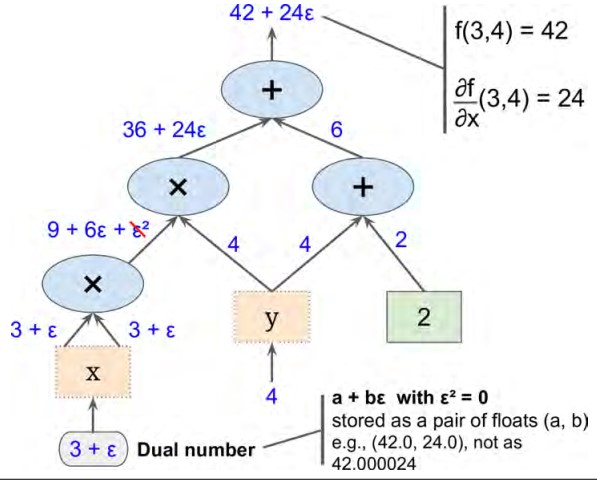
上图给出了使用前向求导方法计算出\(f(x,y)\)在x=3,y=4这一点\(\frac{\partial{f}}{\partial{x}}(3,4)\)的偏导,同理求出\(\frac{\partial{f}}{\partial{y}}(3,4)\),图中的思路很清晰就不赘述。前向求导方法相对数值求导来说准确率较高,当和数值求导方法一样如果参数过多的时候效率会比较差,因为这种方法需要遍历整个图。
逆向自动求导法(Reverse-Mode Atuodiff)###
TensorFlow采用的是逆向自动求导方法,该方法首先正向遍历整个图,计算出每个节点的值;然后逆向(从上到下)遍历整个图,计算出节点的偏导值,步骤如下图所示;节点内蓝色的数值表示正向计算出的结果,为了方便表达,我们从下到上,从左到右依次标注为\(n_1\)到\(n_7\),可以看到最后的值\(n_7\)(顶部节点)为42。
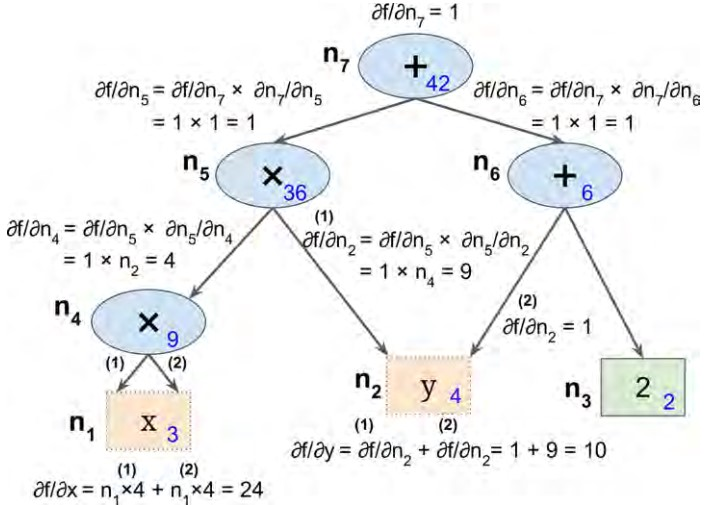
在逆向求导过程中使用链式求导方法:
\(\frac{\partial{f}}{\partial{x}}=\frac{\partial{f}}{\partial{n_i}}{\times}\frac{\partial{n_i}}{\partial{x}}\)
先看节点\(n_7\),作为输出节点\(f=n_7\),所以导数值为\(\frac{\partial{f}}{\partial{n_7}}=1\),
接着向下计算\(n_5\),\(\frac{\partial{f}}{\partial{n_5}}=\frac{\partial{f}}{\partial{n_7}}{\times}\frac{\partial{n_7}}{\partial{n_5}}\),上一步计算出\(\frac{\partial{f}}{\partial{n_7}}=1\),现在我们只需要计算\(\frac{\partial{n_7}}{\partial{n_5}}\),从图中我们知道\(n_7=n_5+n_6\),可以得出\(\frac{\partial{f}}{\partial{x}}=1\)。所以\(\frac{\partial{f}}{\partial{n_5}}=1\),接下来的步骤可以看上面的图,这里就不赘述了。
逆向自动求导法这种方法十分强大且准确率较高,尤其是有却多的输入。这种发方法仅需要正向和逆向遍历一次即可,这种方法更强大的地方在于能够解决符号求解法中硬代码的问题。





 浙公网安备 33010602011771号
浙公网安备 33010602011771号