ABC433

比赛传送门：https://atcoder.jp/contests/abc433

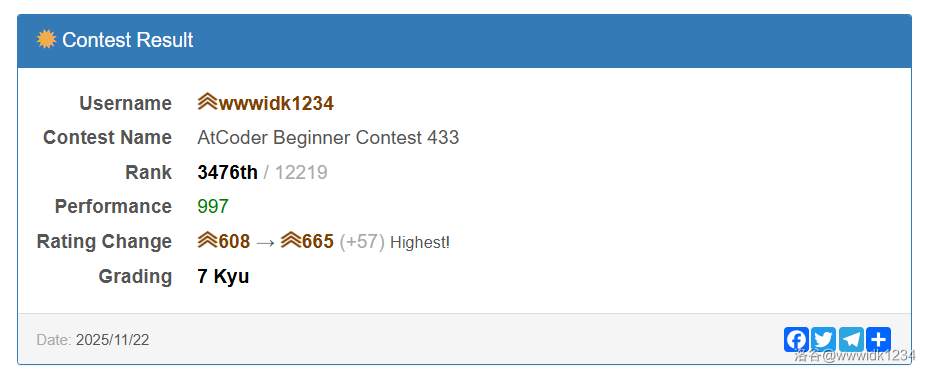
各题 AC 用时：

A	B	C	D
3min	4.5min	26min	54min

反思：C、D 用时过长，D 因为数组开小然后写了个对拍拍了一组数据就发现出问题了。需要加强一次写对代码的能力和思维速度。

A、B 送分题跳过。

C

可以想到处理每一个极大的 1122 子串 \(s^\prime\)（指无法再向左右扩展的连续 1122 型子串），考虑每一个这样的子串，可以一左一右、二左二右地组合成子串，所以每一个这样的子串可以产生 \(\dfrac{|s^\prime|}{2}\) 的贡献。

比如样例：7788788，极大的 1122 子串有 7788、78，对于第一个子串，可以取中间那一段 78 和一整段 7788 一共产生 \(2\) 的贡献，然后 78 可以产生 \(1\) 的贡献。

直接这么做好像有点不好实现。考虑换一个实现方式：将原字符串剖分成若干段 \(t_1,t_2,\cdots,t_n\)，每一段连续的数字都剖出一段，然后扫一遍，如果 \(t_i+1=t_{i+1}\)（即让 \(t_i\) 做前面的“1”、\(t_{i+1}\) 做后面的“2”）的话，就可以产生 \(\min \left\{ \left|t_{i}\right|,\left|t_{i+1}\right|\right\}\) 的贡献。然后做完了。

https://atcoder.jp/contests/abc433/submissions/71145739

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
constexpr int N=1e6+7;
int n;
string s;
vector<string> t;
int main()
{
    // freopen("neuvillette.in","r",stdin);
    // freopen("neuvillette.out","w",stdout);
    cin.tie(0)->sync_with_stdio(0);
    cin>>s;
    n=s.size();
    ll cnt=0;
    string tmp;
    for(int i=0;i<n;i++)
    {
        if(i>0&&s[i]!=s[i-1])
        {
            t.push_back(tmp);
            tmp.clear();
        }
        tmp.push_back(s[i]);
    } t.push_back(tmp);
    for(int i=0;i<int(t.size())-1;i++)
    {
        if(t[i][0]+1==t[i+1][0]) cnt+=min(t[i].size(),t[i+1].size());
    }
    cout<<cnt;
    cout.flush();
    return 0;
}
/*
- 标题 『C - 1122 Substring 2』 
- 链接 『https://atcoder.jp/contests/abc433/tasks/abc433_c』
- 时限 『2000 ms』
- 用时 『h min』
- 思路：

对于每一个极大的1122子串，计算贡献：
000 1111 2222
*/

D

双倍经验：CF1029D ≌ ABC433D

神秘数学题，赛时 10min 出想法，但是实现写了半天，交了一发 RE 了，写了个对拍结果第一组就出问题，发现数组开小了，改了一下过了发现没时间了，于是 AC ABCD rank 3505 遗憾离场（

记长度 \(\operatorname{len}(x)\) 表示数 \(x\) 转成字符串的长度。

首先发现：

\[f(x,y) \bmod m \\ =x \times 10^{\operatorname{len}(b)} \bmod m + y \bmod m \]

因为 \(f(x,y) \bmod m = 0\)，所以我们要配对 \(x \times 10^{\operatorname{len}(y)} \bmod m, y \bmod m\)，使得这两个东西加起来模 \(m\) 为 \(\bold 0\)。

发现这个 \(\operatorname{len}(y)\) 很烦人，但是值域只有 \(10\)，所以考虑钦定这个 \(\operatorname{len}(y)=t\) 每一次处理同一个长度 \(t\) 的 \(y\)。

关于配对，有一个很典的 trick：考虑开一个桶标记其中一个然后枚举另外一个统计（比如 CSP-J 2025 T3 这一题）

于是我们可以考虑开一个桶统计 \(a_i \bmod m=0,1,2,\cdots(\operatorname{len}(a_i)=k)\) 的数量，然后枚举每个 \(a_i\)，统计桶中 \(m-x \times 10^t \bmod m\) 的数量（特别地，要特判一下 \(x \times 10^t \bmod m =0\) 的情况，此时只需统计桶中 \(0\) 的数量即可）计算贡献即可。

https://atcoder.jp/contests/abc433/submissions/71166050

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
constexpr int N=2e5+7;
unordered_map<ll,ll> cnt;
ll a[N];
ll s[15];  //10^i % m =s[i]
int n;
ll m;
inline ll ksm(ll a,ll b)
{
    ll res=1;
    while(b)
    {
        if(b&1) res=res*a%m;
        a=a*a%m;
        b>>=1;
    }
    return res%m;
}
int l[N];
int main()
{
    // freopen("neuvillette.in","r",stdin);
    // freopen("neuvillette.out","w",stdout);
    cin.tie(0)->sync_with_stdio(0);
    cin>>n>>m;
    for(int i=1;i<=n;i++) cin>>a[i];
    for(int i=1;i<=n;i++) l[i]=to_string(a[i]).size();
    for(int i=0;i<=10;i++) s[i]=ksm(10,i);
    ll ans=0;
    bool is=0;
    for(int len=1;len<=10;len++)
    {
        cnt.clear(); is=0;
        for(int i=1;i<=n;i++)
        {
            if(l[i]==len) is=1,cnt[a[i]%m]++;
        }
        if(!is) continue;
        for(int i=1;i<=n;i++)
        {
            ll contribute=cnt[m-((a[i]%m*s[len])%m)];
            if((a[i]%m*s[len])%m==0) contribute+=cnt[0];
            // cerr<<a[i]<<" contributed "<<contribute<<" len="<<len<<endl;
            ans+=contribute;
        }
    }
    cout<<ans<<endl;
    cout.tie(0);
    return 0;
}
/*
- 标题 『D - 183183』 
- 链接 『https://atcoder.jp/contests/abc433/tasks/abc433_d』
- 时限 『2000 ms』
- 用时 『h min』
- 思路：
f(a,b)=a*10^{len(b)}+b
考虑钦定b找a
f(a,b)%m=a%m * 10^{len(b)}%m + b%m = m
用map标记a%m * 10^{len(b)}%m=k的个数
*/

CF