OpenCV-Python系列之相机校准

其实大家可能已经发现，越到后面，所涉及的跟视频处理都有很大的关系，包括特征点，目标跟踪以及光流等等这些东西。

在本次教程中，我们将介绍：

· 由相机引起的失真类型，

· 如何找到相机的固有和非固有特性

· 如何根据这些特性使图像不失真

一些针孔相机会给图像带来明显的失真。两种主要的变形是径向变形和切向变形。径向变形会导致直线出现弯曲。

距图像中心越远，径向畸变越大。例如，下面显示一个图像，其中棋盘的两个边缘用红线标记。但是，我们会看到棋盘的边框不是直线，并且与红线不匹配，所有预期的直线都凸出。

径向变形可以表示成如下：

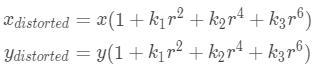
同样，由于摄像镜头未完全平行于成像平面对齐，因此会发生切向畸变。因此，图像中的某些区域看起来可能比预期的要近。切向畸变的量可以表示为：

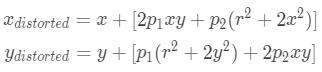
简而言之，我们需要找到五个参数，称为失真系数，公式如下：

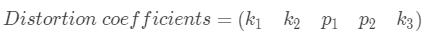
除此之外，我们还需要其他一些信息，例如相机的内在和外在参数。内部参数特定于摄像机。它们包括诸如焦距(f_x,f_y)和光学中心(c_x,c_y)之类的信息。焦距和光学中心可用于创建相机矩阵，该相机矩阵可用于消除由于特定相机镜头而引起的畸变。相机矩阵对于特定相机而言是唯一的，因此一旦计算出，就可以在同一相机拍摄的其他图像上重复使用。它表示为3x3矩阵：

外在参数对应于旋转和平移矢量，其将3D点的坐标平移为坐标系。

对于立体声应用，首先需要纠正这些失真。要找到这些参数，我们必须提供一些定义良好的图案的示例图像（例如国际象棋棋盘）。我们找到一些已经知道其相对位置的特定点（例如棋盘上的四角）。我们知道现实世界空间中这些点的坐标，也知道图像中的坐标，因此我们可以求解失真系数。为了获得更好的结果，我们至少需要10个测试模式。

相机校准原理

首先先简单的了解一下相机标定的原理。
摄像机标定(Camera calibration)简单来说是从世界坐标系换到图像坐标系的过程，也就是求最终的投影矩阵 P 的过程。

一般来说，标定的过程分为两个部分：

· 第一步是从世界坐标系转换为相机坐标系，这一步是三维点到三维点的转换，包括 R，t （相机外参）等参数；

· 第二部是从相机坐标系转为图像坐标系，这一步是三维点到二维点的转换，包括 K（相机内参）等参数；

世界坐标系转换为相机坐标系：

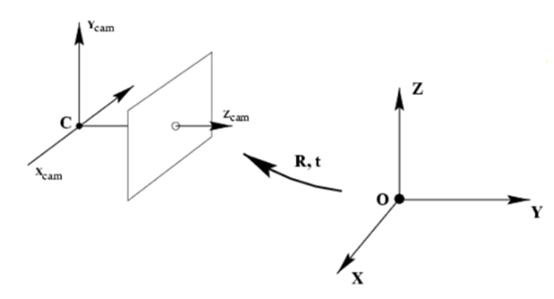
公式表达如下：

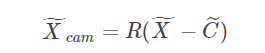
其中：

相机坐标系转换为图像坐标系：

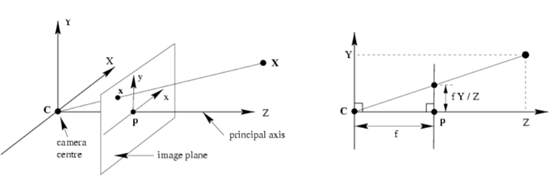
其中：

· C点表示camera centre，即相机的中心点，也是相机坐标系的中心点；

· Z 轴表示principal axis，即相机的主轴；

· p 点所在的平面表示image plane，即相机的像平面，也就是图片坐标系所在的二维平面；

· p点表示principal point，即主点，主轴与像平面相交的点；

· C 点到 p 点的距离，也就是右边图中的f 表示focal length，即相机的焦距；

· 像平面上的 x 和 y 坐标轴是与相机坐标系上的 X 和 Y 坐标轴互相平行的；

· 相机坐标系是以 X， Y， Z三个轴组成的且原点在 C 点，度量值为米（m）；

· 像平面坐标系是以 x，y（小写）两个轴组成的且原点在 p 点，度量值为米（m）；

· 图像坐标系一般指图片相对坐标系，在这里可以认为和像平面坐标系在一个平面上，不过原点是在图片的角上，而且度量值为像素的个数（pixel）；

通过对上面坐标系的介绍，可以得到以下的转换公式：

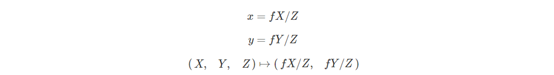
加上偏移量：

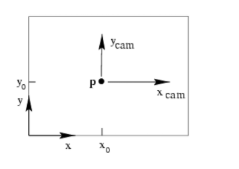
如上图所示，其中主点 p 是像平面坐标系的原点，但在图像坐标系中的位置为 (px,py)，在这里，图形坐标系的原点是图片的左下角，所以可以得到：

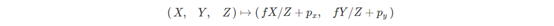
把这个换成矩阵计算：

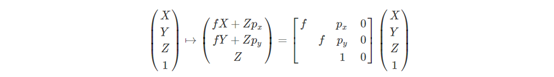
整理一下：

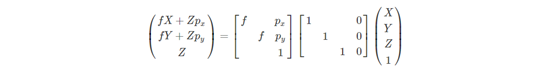
最后，可以得到矩阵K，就是相机内参：

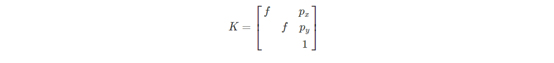
投影矩阵P（在这里可以认为旋转矩阵 R 为单位矩阵 I，平移矩阵 t 都为0）：

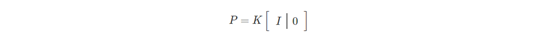
从上面两个转换的过程，我们可以得到从世界坐标轴转换到图像的过程可以把投影矩阵P表示为：

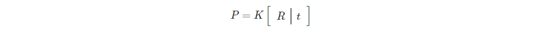
其中：

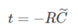
在这里，K 一般称为相机内参，描述了相机的内部参数，包括焦距 f、主点 p 的位置、以及像素与真实环境的大小比例等，这个是固有属性，是提供好的；R 和 t 称为相机外参，R 在这里是旋转矩阵，可以转换为三维的旋转向量，分别表示绕x，y，z 三个轴的旋转角度，t 目前就是一个平移向量，分别表示在x，y，z 三个方向上的平移量。

了解完一定原理之后，我们在下个教程中将开始实践一下。