选择排序
选择排序
来自济南黑马程序员数据与算法教程
一、选择排序
是一种更加简单直观的排序方法
1. 排序原理:
1.每一次遍历的过程中,都假定第一个索引处的元素是最小值,和其他索引处的值依次进行比较,如果当前索引处的值大于其他某个索引处的值,则假定其他某个索引出的值为最小值,最后可以找到最小值所在的索引
2.交换第一个索引处和最小值所在的索引处的值

enter description here
2. 代码
import java.util.Arrays;
/**
* @author shkstart
* @create 2022-03-03 16:52
*/
public class Main {
public static void main(String[] args) {
Integer[] arr = {4,3,2,10,12,1,5,6};
sort(arr);
}
public static void sort(Comparable[] a){
for (int i = 1; i < a.length; i++) {
for (int j = i; j > 0; j--) {
if (greater(a[j - 1],a[j])){
exch(a,j - 1,j);
}else {
break;
}
}
System.out.println(Arrays.toString(a));
}
}
//判断v比w大
private static boolean greater(Comparable v,Comparable w){
return v.compareTo(w)>0;
}
private static void exch(Comparable[] a,int i,int j){
Comparable temp;
temp = a[i];
a[i] = a[j];
a[j] = temp;
}
}
二、堆排序
1. 1.1 堆的定义
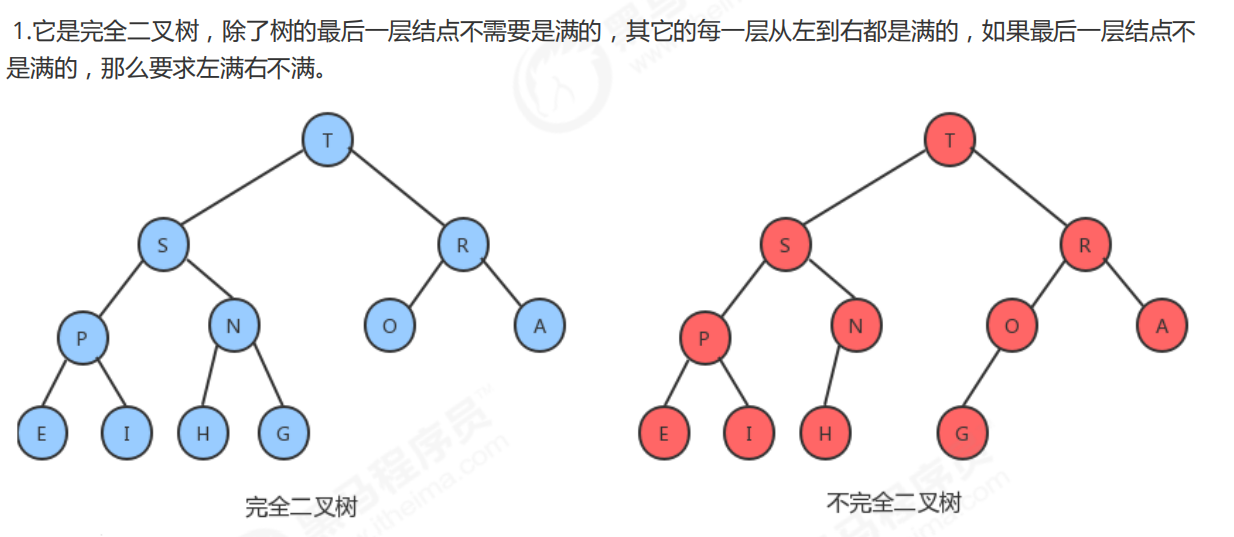
- 堆是计算机科学中一类特殊的数据结构的统称,堆通常可以被看做是一棵完全二叉树的数组对象。
![enter description here enter description here]()
2.它通常用数组来实现。
具体方法就是将二叉树的结点按照层级顺序放入数组中,根结点在位置1,它的子结点在位置2和3,而子结点的子结点则分别在位置4,5,6和7,以此类推。
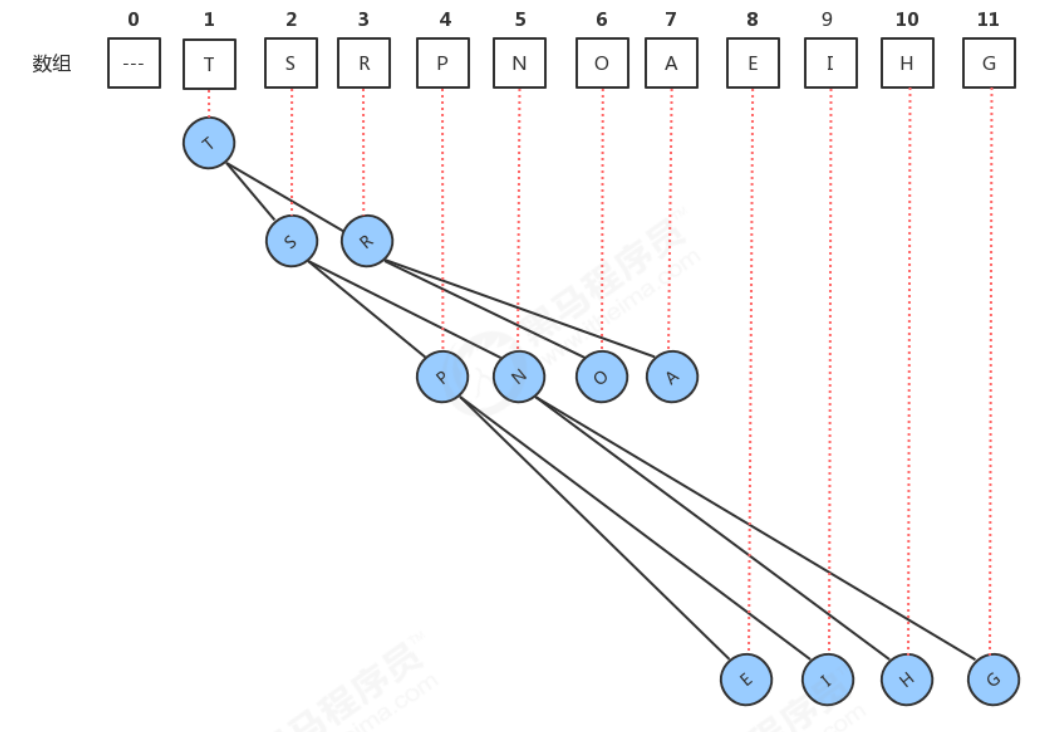
enter description here
- 当前节点为k,他父节点[k/2],两个子结点的位置则分别为[2k]和[2k+1]
- 每个结点都大于等于它的两个子结点。这里要注意堆中仅仅规定了每个结点大于等于它的两个子结点,但这两个子结点的顺序并没有做规定,跟我们之前学习的二叉查找树是有区别的。
2. 堆排序过程
对构造好的堆,我们只需要做类似于堆的删除操作,就可以完成排序。
1.将堆顶元素和堆中最后一个元素交换位置;
2.通过对堆顶元素下沉调整堆,把最大的元素放到堆顶(此时最后一个元素不参与堆的调整,因为最大的数据已经到了数组的最右边)
3.重复1~2步骤,直到堆中剩最后一个元素。
这里我们是最大值在根节点
现在看这个堆的下沉,这是堆排序的核心(不断的和下面的比)
target是我们需要下沉的元素,range是范围
//在heap堆中,对target处的
//元素做下沉,范围是0~range。
private static void sink(Comparable[] heap, int target, int range) {
//没有子结点了
while (2*target<=range){
//寻找最大值
int max;
//我们先判断有没有右子树,如果有右子树则一定会有左子树
//因为2个子树是没有顺序的,所以插入的时候先填写左子树,后填入右子树
if (2*target+1<=range){
if (less(heap,2*target,2*target+1)){
max=2*target+1;
}else {
max=2*target;
}
}else {
max = 2*target;
}
if (!less(heap,target,max)){
break;
}
exch(heap,target,max);
target = max;
}
}解析这段代码:这段代码是在堆创建并排序完成后的
先把首节点也就是最大的节点与尾节点交换,然后N--,此时交换后的节点不参与下沉排序
这样如此循环后,就是一个递增的数组
while (N!=1){
exch(heap,1,N);
N--;
sink(heap,1,N);
}
package 堆;
public class HeapSort {
//对source数组中的数据从小到大排序
public static void sort(Comparable[] source) {
//source.length + 1是因为堆的第一个要为空
Comparable[] heap = new Comparable[source.length + 1];
createHeap(source,heap);
//长度为12,第一个元素为空,所以也得是length-1
int N=heap.length - 1;
while (N!=1){
exch(heap,1,N);
N--;
sink(heap,1,N);
}
System.arraycopy(heap,1,source,0,source.length);
}
//根据原数组 source,构造出堆heap
private static void createHeap(Comparable[] source, Comparable[] heap) {
//拷贝source数组从0开始拷贝到heap从1开始,长度为source的长度
System.arraycopy(source,0,heap,1,source.length);
//从索引的的一半开始下层,索引的一半都是倒数第二层,因为最后一层是N=heap.length,而最后一层的上一层就是N/2
//由于堆的第一个元素为空,length-1就能得到堆的最后一个元素
//由于是下沉,不断的和下面的元素进行比较,所以最后一行不需要比较,只需要从倒数第二层开始下层
for (int i =(heap.length-1)/2; i > 0; i--) {
//复制的时候从1开始到source.length,使得最后一个元素为空
sink(heap,i,heap.length - 1);
}
}
// i<j为ture
private static boolean less(Comparable[] heap, int i, int j) {
return heap[i].compareTo(heap[j]) < 0;
}
private static void exch(Comparable[] heap, int i, int j) {
Comparable temp = heap[i];
heap[i] = heap[j];
heap[j] = temp;
}
}
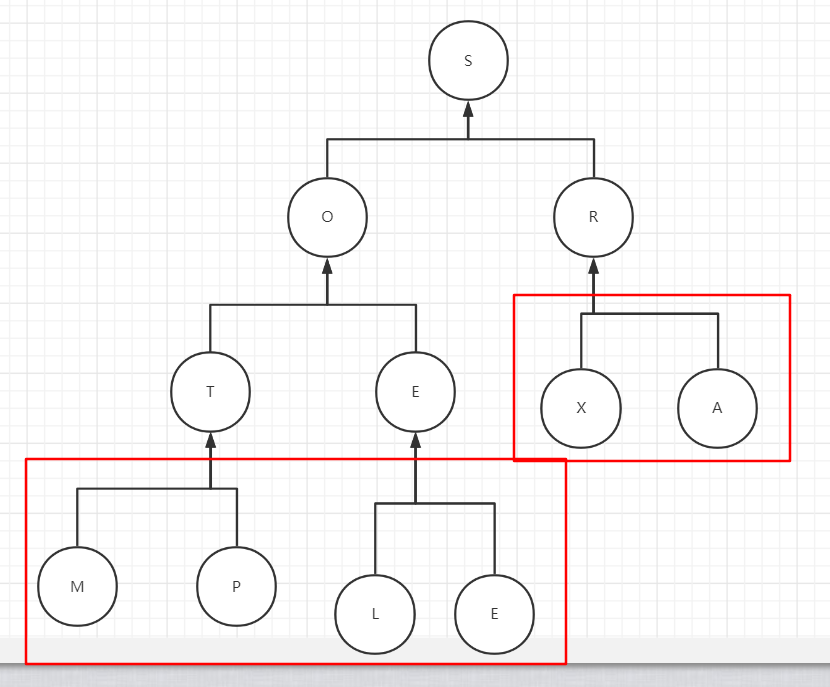
(heap.length-1)/2的解释:根据最后一个元素返回最后一个父节点也就是E
红色框框里面的不参与排序
这个图有11个元素,但是0号下标为空元素,所以这个数组是有12个元素的
而尾元素就是12-1也就是11号下标
三、时间空间复杂度分析
1. 选择排序:
选择排序是给每个位置选择当前元素最小的,例如有数据{5(1),8 ,5(2), 2, 9 },第一遍选择到的最小元素为2,所以5(1)会和2进行交换位置,此时5(1)到了5(2)后面,破坏了稳定性,所以选择排序是一种不稳定的排序算法。

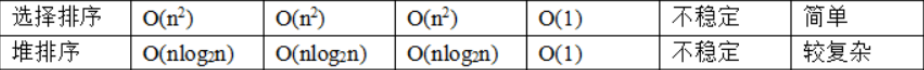



 浙公网安备 33010602011771号
浙公网安备 33010602011771号