背包问题
有 N 件物品和一个容量是 V 的背包。
第 i 件物品的体积是 vi,价值是 wi。
求解将哪些物品装入背包,可使这些物品的总体积不超过背包容量,且总价值最大。
输出最大价值。
01背包问题(每个物品只能拿0或1次)
输入格式
第一行两个整数,N,V,用空格隔开,分别表示物品数量和背包容积。
接下来有 N 行,每行两个整数 vi,wi,用空格隔开,分别表示第 i 件物品的体积和价值。
输出格式
输出一个整数,表示最大价值。
数据范围
0<N,V≤1000
0<vi,wi≤1000
输入样例
4 5
1 2
2 4
3 4
4 5
输出样例:
8
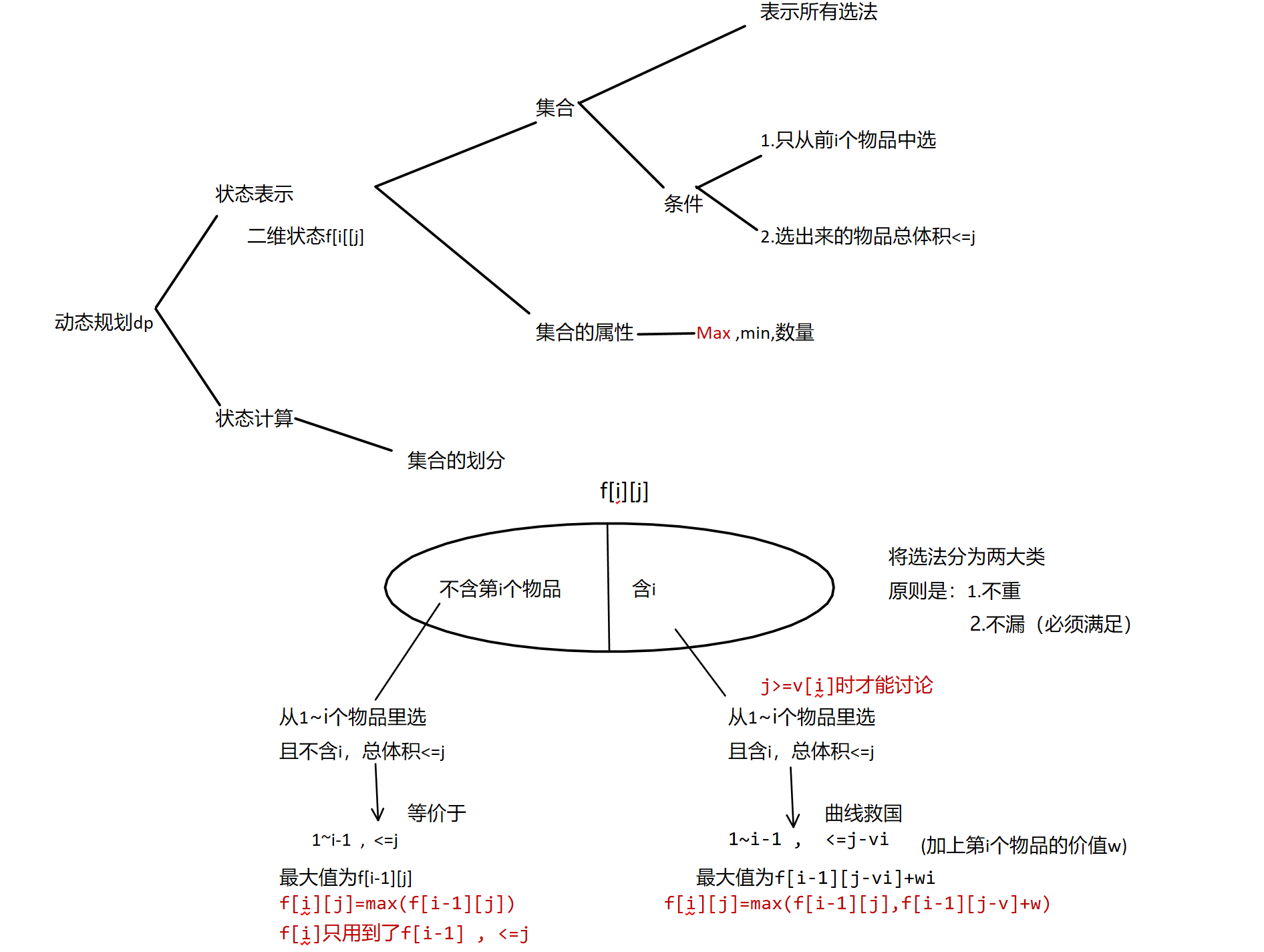
朴素写法
for(int i = 1; i <= n; i++)
for(int j = 1 ; j <= m ; j++)
if(j < v[i]) f[i][j] = f[i-1][j];
else
f[i][j] = max(f[i-1][j], f[i-1][j - v[i]] + w[i]);
如何优化呢?
将状态f[i][j]优化到一维f[j]
1.注意枚举背包容量j必须从m开始。
2.为什么一维情况下枚举背包容量需要逆序?
在二维情况下,状态f[i][j]是由上一轮i - 1的状态得来的,f[i][j]与f[i - 1][j]是独立的。而优化到一维后,如果我们还是正序,则有f[较小体积]更新到f[较大体积],则有可能本应该用第i-1轮的状态却用的是第i轮的状态。
3.简单来说,一维情况正序更新状态f[j]需要用到前面计算的状态已经被「污染」,逆序则不会有这样的问题。
状态转移方程为:f[j] = max(f[j], f[j - v[i]] + w[i] 。
优化(一维)后代码
#include<bits/stdc++.h>
using namespace std;
const int N = 1005;
int v[N]; // 体积
int w[N]; // 价值
int f[N]; // f[i][j], j体积下前i个物品的最大价值
int main()
{
int n, m;
cin >> n >> m;
for(int i = 1; i <= n; i++)
cin >> v[i] >> w[i];
for(int i = 1; i <= n; i++)
for(int j = m; j>=v[i]; j--)
f[j] = max(f[j], f[j - v[i]] + w[i]);
cout << f[m] << endl;
return 0;
}
完全背包问题(每件物品有无限个)
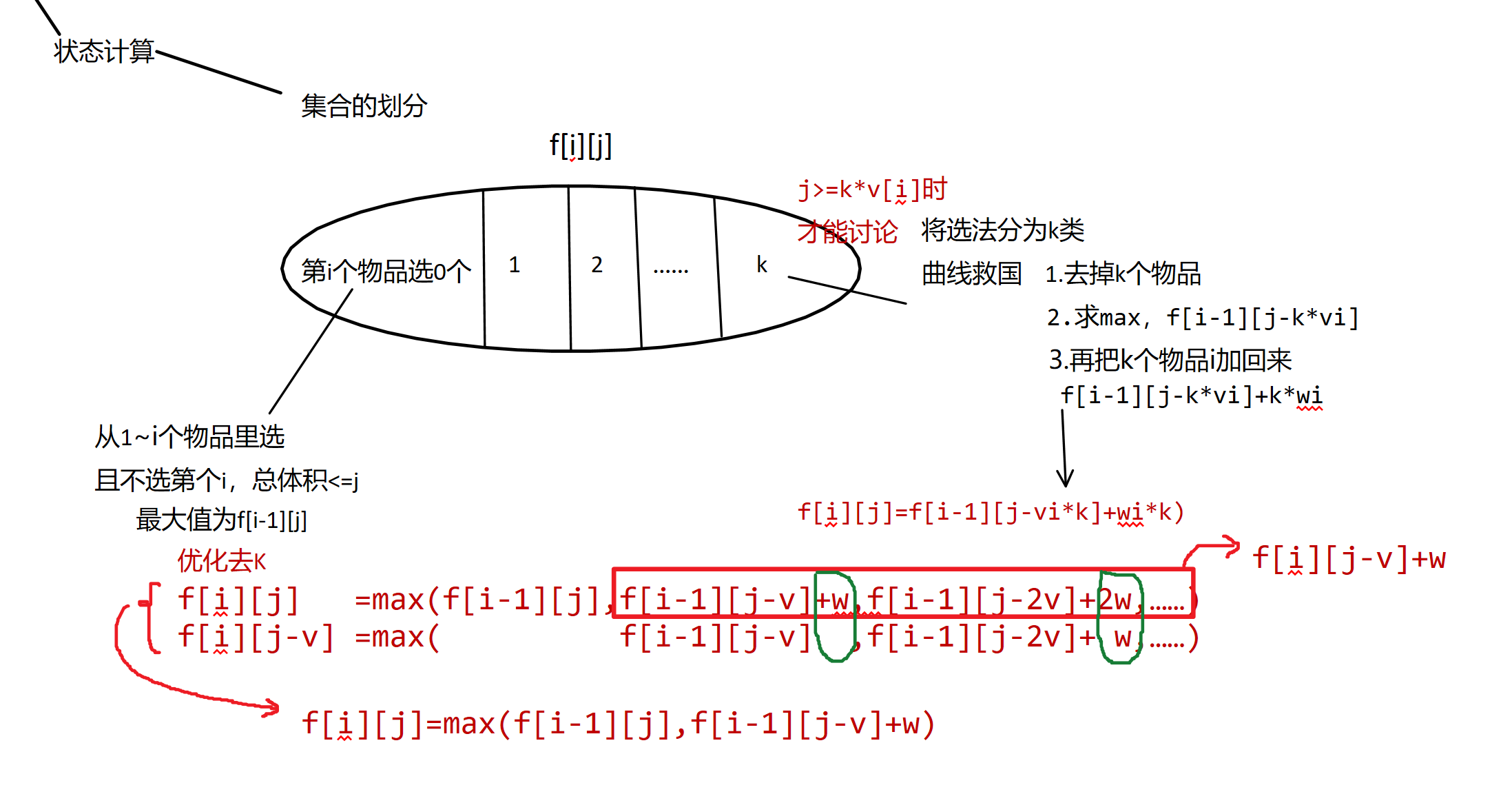
朴素写法
for(int i = 1 ; i <= n ; i++)
for(int j = 0 ; j <= m ; j++)
for(int k = 0 ; k * v[i] <= j ; k++)
f[i][j] = max(f[i-1][j] , f[i-1][j-v[i]*k] + w[i]*k);
优化后(去k,化一维)后代码
#include<bits/stdc++.h>
using namespace std;
const int N = 1005;
int v[N]; // 体积
int w[N]; // 价值
int f[N]; // f[i][j], j体积下前i个物品的最大价值
int main()
{
int n, m;
cin >> n >> m;
for(int i = 1; i <= n; i++)
cin >> v[i] >> w[i];
for(int i = 1; i <= n; i++)
for(int j = v[i]; j<=m; j++)
f[j] = max(f[j], f[j - v[i]] + w[i]);
cout << f[m] << endl;
return 0;
}
多重背包问题(每个物品最多有si个,每个物品对应的si不一样)
输入格式
第一行两个整数,N,V,用空格隔开,分别表示物品种数和背包容积。
接下来有 N 行,每行三个整数 vi,wi,si,用空格隔开,分别表示第 i 种物品的体积、价值和数量。
输出格式
输出一个整数,表示最大价值。
数据范围
0<N,V≤100
0<vi,wi,si≤100
输入样例
4 5
1 2 3
2 4 1
3 4 3
4 5 2
输出样例:
10
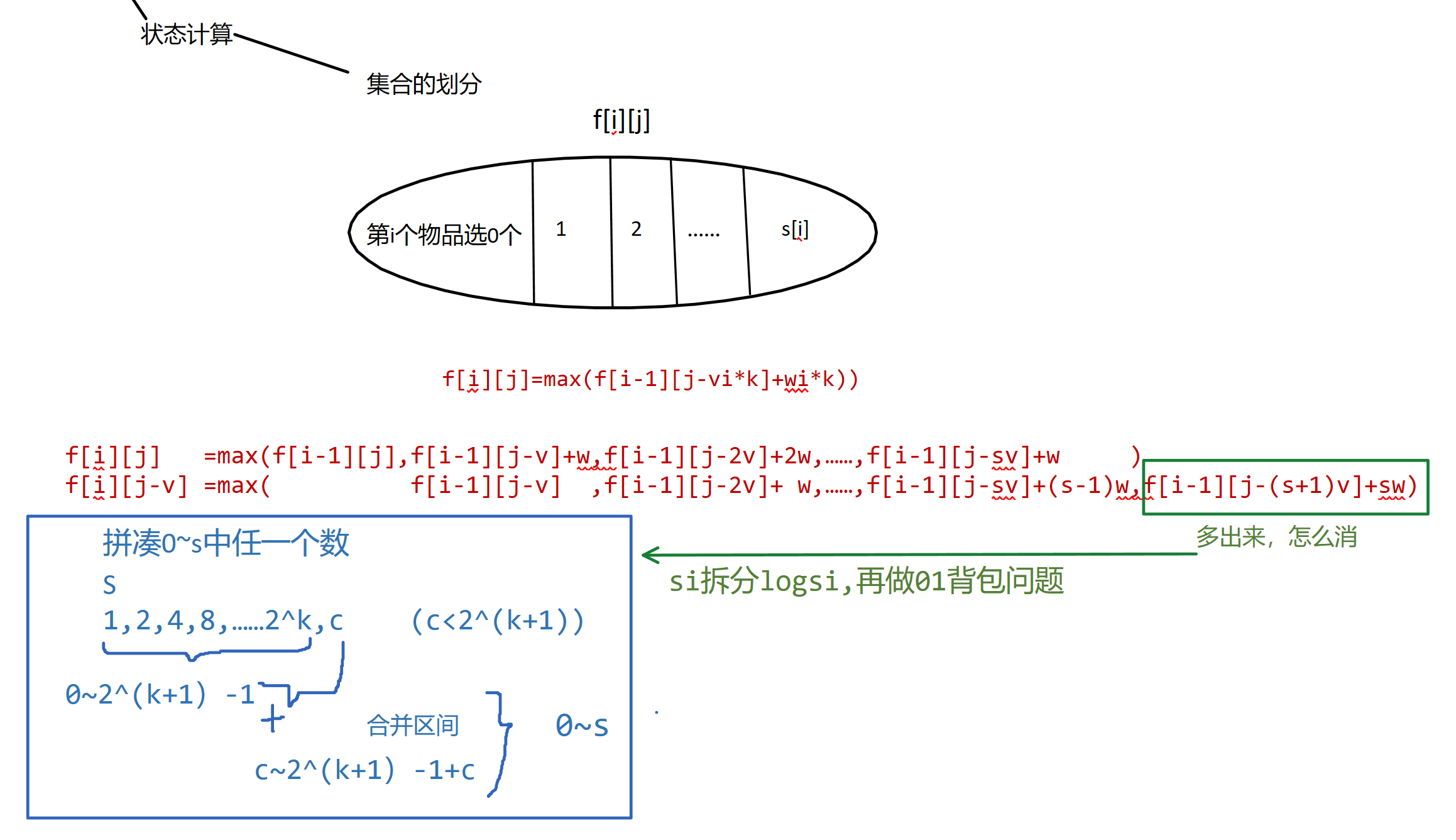
朴素写法
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 110;
int v[N], w[N], s[N];
int f[N][N];
int n, m;
int main(){
cin >> n >> m;
for(int i = 1; i <= n; i ++) cin >> v[i] >> w[i] >> s[i];
for(int i = 1; i <= n; i ++){//枚举背包
for(int j = 1; j <= m; j ++){//枚举体积
for(int k = 0; k <= s[i]&&k*v[i]<=j; k ++){
if(j >= k * v[i]){
f[i][j] = max(f[i][j], f[i - 1][j - k * v[i]] + k * w[i]);
}
}
}
}
cout << f[n][m] << endl;
return 0;
}
优化后代码
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 250000, M = 5000;
int v[N], w[N], s[N];
int f[N];
int n, m, cnt = 0;
int main() {
cin >> n >> m;
for (int i = 1; i <= n; i ++) {
int a, b, s;
cin >> a >> b >> s;
int k = 1;
while (k <= s) {
cnt++;
v[cnt] = a * k;
w[cnt] = b * k;
s -= k;
k *= 2;
}
if (s > 0) {
cnt++;
v[cnt] = a * s;
w[cnt] = b * s;
}
}
n = cnt;
for (int i = 1; i <= n; i ++)
for (int j = m; j >= v[i]; j --)
f[j] = max(f[j], f[j - v[i]] + w[i]);
cout << f[m] << endl;
return 0;
}
分组背包问题(有N组物品,每组有若干个物品,同一组内的物品最多选一种)
有 N 组物品和一个容量是 V 的背包。
每组物品有若干个,同一组内的物品最多只能选一个。
每件物品的体积是 vij,价值是 wij,其中 i 是组号,j 是组内编号。
求解将哪些物品装入背包,可使物品总体积不超过背包容量,且总价值最大。
输出最大价值。
输入格式
第一行有两个整数 N,V,用空格隔开,分别表示物品组数和背包容量。
接下来有 N 组数据:
每组数据第一行有一个整数 Si,表示第 i 个物品组的物品数量;
每组数据接下来有 Si 行,每行有两个整数 vij,wij,用空格隔开,分别表示第 i 个物品组的第 j 个物品的体积和价值;
输出格式
输出一个整数,表示最大价值。
数据范围
0<N,V≤100
0<Si≤100
0<vij,wij≤100
输入样例
3 5
2
1 2
2 4
1
3 4
1
4 5
输出样例:
8
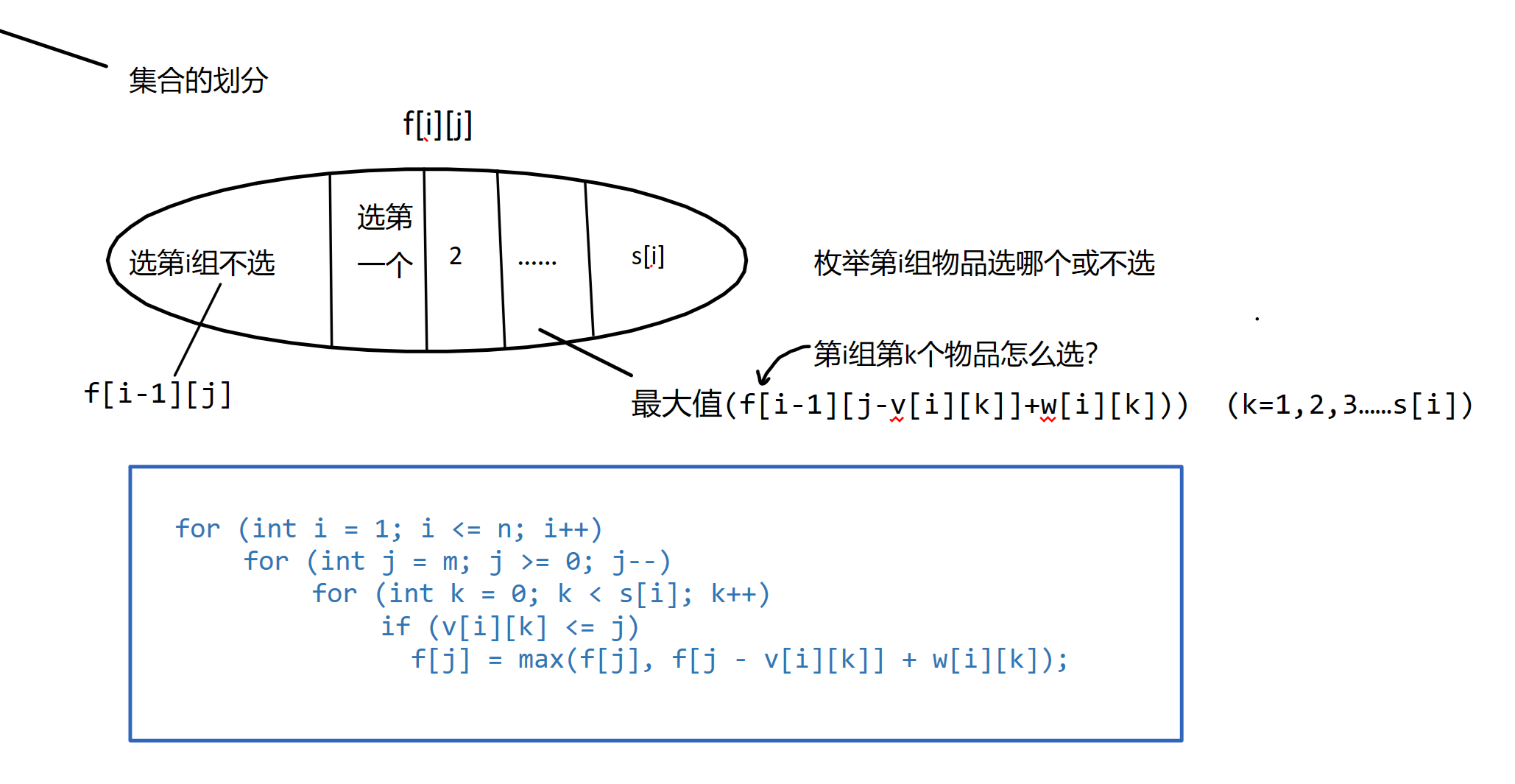
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 110;
int v[N][N], w[N][N], s[N];
int f[N];
int n, m;
int main() {
cin >> n >> m;
for (int i = 1; i <= n; i++) {
cin >> s[i];
for (int k = 0; k < s[i]; k++)
cin >> v[i][k] >> w[i][k];
}
for (int i = 1; i <= n; i++)
for (int j = m; j >= 0; j--)
for (int k = 0; k < s[i]; k++)
if (v[i][k] <= j)
f[j] = max(f[j], f[j - v[i][k]] + w[i][k]);
cout << f[m] << endl;
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号