广搜
概念
广搜,即广度优先搜索(BFS)是连通图的一种遍历策略。它的思想是从一个顶点V0开始,辐射状的优先遍历其周围较广的区域。
连通图示意图
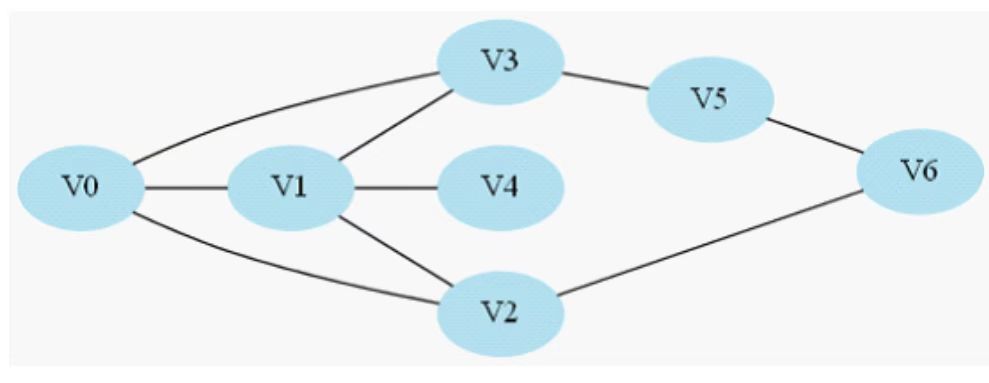
可以看出从V0到V6的最短路径是V0->V2->V6
自己是怎么找到这条最短路径的?
——首先看跟V0直接连接的节点V1,V2,V3.发现没有V6进而再看看刚刚V1,V2,V3的直接连接节点。V1,V2,V3的直接连接节点分别是{V0,V4},{V0,V1,V6},{V0,V1,V5}.这时候我们在V2的直接节点中发现了V6,说明V0->V2->V6就是最短路径。
广搜
算法的基本思路
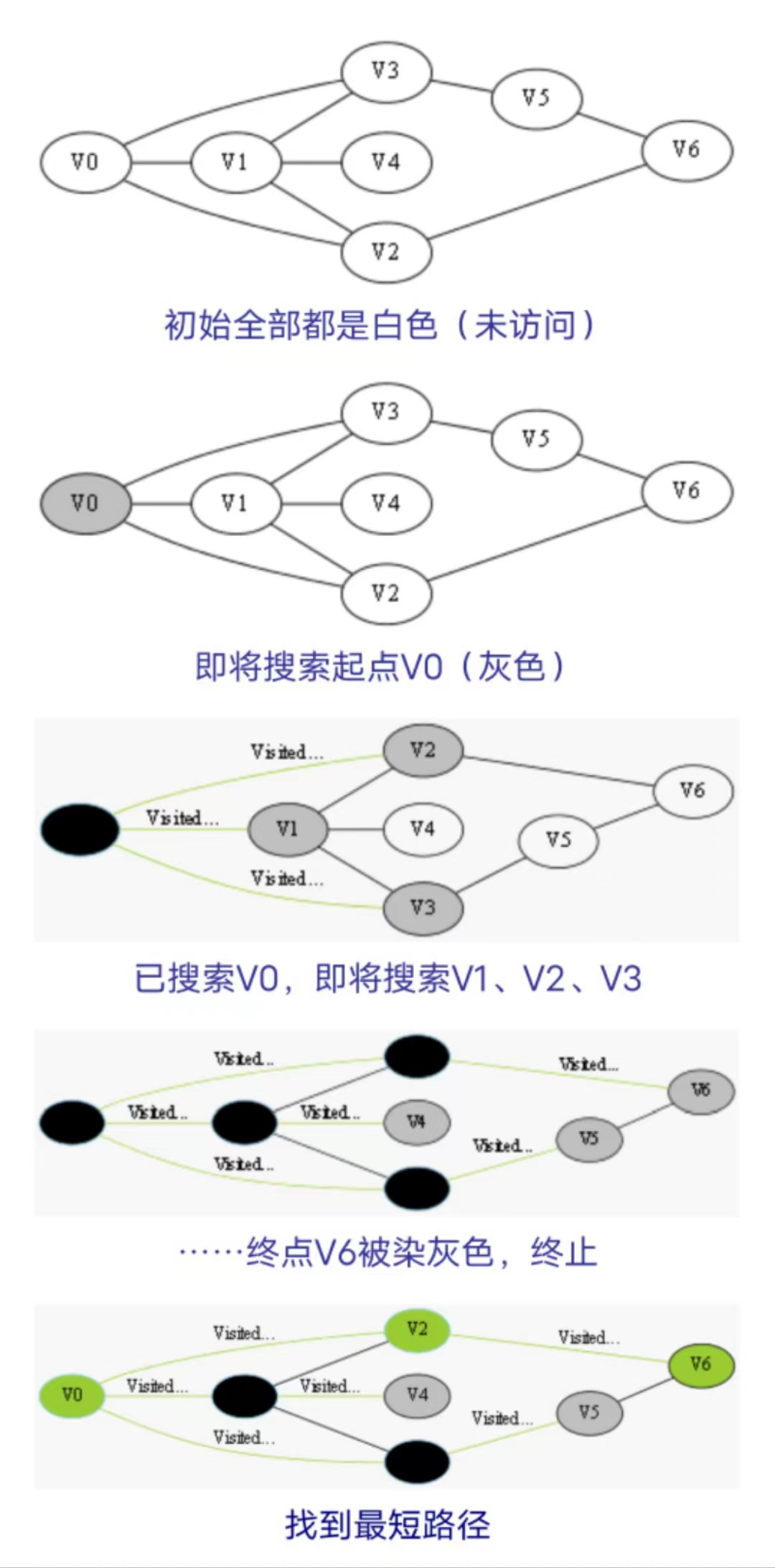
看如下示例图
在搜索的过程中,初始所有节点是白色(表示所有点都还没开始搜索),把起点VO标志成灰色(表示即将辐射V0),下一步搜索的时候,我们把所有的灰色节点访问次,然后将其变成黑色(表示已经被辐射过了),进而再将他们所能到达的节点标志成灰色(因为那些节点是下一步搜索的目标点),但是这里有个判断,就像刚刚的例子,当访问到V1节点的时候,它的下一个节点应该是VO和V4,但是VO已经在前面被染成黑色了,所以不会将它染灰色。这样持续下去,直到目标节点V6被染灰色,说明了下一步就到终点了,没必要再搜索(染色)其他节点了,此时可以结束搜索了,整个搜索就结束了。然后根据搜索过程,反过来把最短路径找出来,图中把最终路径上的节点标志成绿色。
例子:AcWing 844. 走迷宫
给定一个 n×m 的二维整数数组,用来表示一个迷宫,数组中只包含 0 或 1,其中 0 表示可以走的路,1 表示不可通过的墙壁。
最初,有一个人位于左上角 (1,1) 处,已知该人每次可以向上、下、左、右任意一个方向移动一个位置。请问,该人从左上角移动至右下角 (n,m) 处,至少需要移动多少次。
数据保证 (1,1) 处和 (n,m) 处的数字为 0,且一定至少存在一条通路。
输入格式
第一行包含两个整数 n 和 m
接下来 n 行,每行包含 m 个整数(0 或 1),表示完整的二维数组迷宫。
输出格式
输出一个整数,表示从左上角移动至右下角的最少移动次数。
数据范围
1≤n,m≤100
输入样例:
5 5
0 1 0 0 0
0 1 0 1 0
0 0 0 0 0
0 1 1 1 0
0 0 0 1 0
输出样例:
8
思路
从起点开始,往前走第一步,记录下所有第一步能走到的点,然后从所第一步能走到的点开始,往前走第二步,记录下所有第二步能走到的点,重复下去,直到走到终点。输出步数即可。

这就是广度优先遍历的思路。
实现方式:广度优先遍历
1.用 g 存储地图,f 存储起点到其他各个点的距离。
2.从起点开始广度优先遍历地图。
3.当地图遍历完,就求出了起点到各个点的距离,输出f[n][m]即可。
搜索的顺序就是第一层->第二层->第三层->...->第N层 假设终点在第N层,那么搜索到的最短路径一定是N;
void bfs(int a, int b): 广度优遍历函数。输入的是起点坐标。
queue<PII> q;:用来存储每一步走到的点。
while(!q.empty())循环:循环依次取出同一步数能走到的点,再往前走一步。
int dx[4] = {0, 1, 0, -1}, dy[4] = {-1, 0, 1, 0};:一个点往下一步走得时候,可以往上下左右四方向走。
代码
#include <cstring>
#include <iostream>
#include <queue>
using namespace std;
typedef pair<int, int> PII;
const int N = 110;
int g[N][N];//存储地图
int f[N][N];//存储距离
int n, m;
void bfs(int a, int b)//广度优先遍历
{
queue<PII> q;
q.push({a, b});//队尾插入起点值1,1
while(!q.empty())//队列不为空时,继续循环
{
PII start = q.front();//队头的值赋给pair的第一个数据
q.pop();//队头清零
g[start.first][start.second] = 1;//地图起点处为1(墙)
int dx[4] = {0, 1, 0, -1}, dy[4] = {-1, 0, 1, 0};//上右下左四个方向
for(int i = 0; i < 4; i++)//(x,y)往四个方向走
{
int x = start.first + dx[i], y = start.second + dy[i];
if(g[x][y] == 0)//0表示可以走,1表示不能走(墙),g[x][y]为0说明(x,y)没走过这个点
{
g[x][y] = 1;//那么就走,走过的地方就变成墙(1)
f[x][y] = f[start.first][start.second] + 1;//从当前点走过去,距离+1.
q.push({x, y});//队尾插入x,y(更新为下一步走到的点
}
}
}
//走到最后只有终点是0,其他位置全是1,此时队列为空(0),停止循环
cout << f[n][m];//输出最短距离
}
int main()
{
memset(g, 1, sizeof(g));//memset初始化函数,对数组g初始化,设置元素值全为1(写1,存储的不是1,只要不是 0 或 1 这个题就能用)
//写1是为了把迷宫四周初始化为墙(数字1)了,所以不用做越界判断
cin >> n >>m;
for(int i = 1; i <= n; i++)
{
for(int j = 1; j <= m; j++)
{
cin >> g[i][j];
}
}
bfs(1,1);
}
例二:洛谷-马的遍历
题目描述
有一个n*m的棋盘(1<n,m<=400),在某个点上有一个马,要求你计算出马到达棋盘上任意一个点最少要走几步
输入格式
一行四个数据,棋盘的大小和马的坐标
输出格式
一个n*m的矩阵,代表马到达某个点最少要走几步(左对齐,宽5格,不能到达则输出-1)
样例
输入
3 3 1 1
输出
0 3 2
3 -1 1
2 1 4
分析
求最短路就是广搜,到达某个点的步数就是上个点过来的步数加1,然后马的方向就是可以走8个方向,依次判断是否合法,以及是否已经走过(记得去重),然后加入队列
代码
#include<bits/stdc++.h>
using namespace std;
struct node {
int x, y;
node(int xx, int yy) {
x = xx, y = yy;
}
};
int n, m, x, y;
queue<node> q;
int a[408][408];//存储地图
int vis[408][408];
int dx[] = {-2, -2, -1, 1, 2, 2, 1, -1};//八个方向
int dy[] = {-1, 1, 2, 2, 1, -1, -2, -2};
void bfs() {
q.push(node(x, y));//队尾插入
a[x][y] = 0;//起始点,步数为0
vis[x][y] = 1;//vis标记为1表示走过
while (!q.empty()) {
int x = q.front().x;//返回队列第一个元素
int y = q.front().y;
q.pop();//删除队列第一个元素
//马可以向八个方向走
for (int i = 0; i < 8; i++) {//(xx,yy)表示向八个方向走了之后的点
int xx = x + dx[i];
int yy = y + dy[i];
if (xx >= 1 && yy >= 1 && xx <= n && yy <= m && !vis[xx][yy]) {//判断点是否越界
a[xx][yy] = a[x][y] + 1;//没越界则可以走,步数加一
q.push(node(xx, yy));//队尾插入
vis[xx][yy] = 1;//标记走过
}
}
}
}
int main() {
cin >> n >> m >> x >> y;
memset(a, -1, sizeof a);//全部赋值为-1,用于判断点是否越界
bfs();
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
printf("%-5d", a[i][j]);
}
cout << endl;
}
return 0;
}
例三:数独挑战
玩家需要根据9×9 盘面上的已知数字,推理出所有剩余位置的数字,并满足每一行、每一列、每一个粗线九宫格内的数字包含有 1-9 的数字,且不重复。
现在给你一个数独,请你解答出来。每个数独保证有且只有一个解。
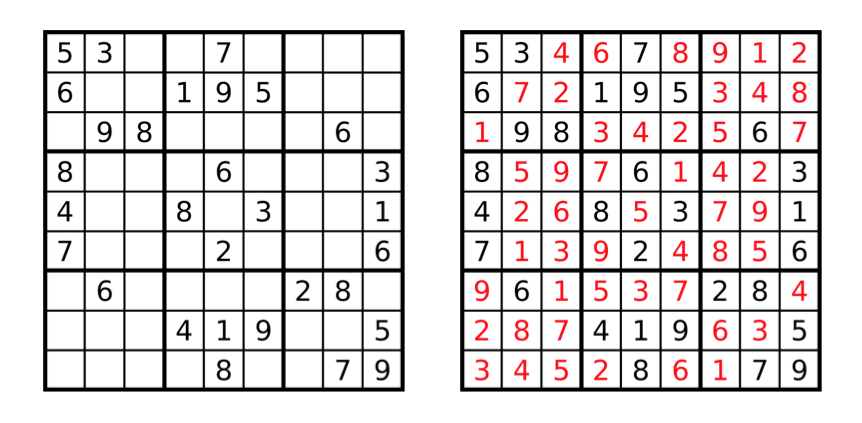
输入描述:
输入仅一组数据,共 9 行 9 列,表示初始数独(其中 0 表示数独中的空位)。
输出描述:
输出共 9 行 9 列,表示数独的解。
注意⾏末没有空格。
输入
5 3 0 0 7 0 0 0 0
6 0 0 1 9 5 0 0 0
0 9 8 0 0 0 0 6 0
8 0 0 0 6 0 0 0 3
4 0 0 8 0 3 0 0 1
7 0 0 0 2 0 0 0 6
0 6 0 0 0 0 2 8 0
0 0 0 4 1 9 0 0 5
0 0 0 0 8 0 0 7 9
输出
5 3 4 6 7 8 9 1 2
6 7 2 1 9 5 3 4 8
1 9 8 3 4 2 5 6 7
8 5 9 7 6 1 4 2 3
4 2 6 8 5 3 7 9 1
7 1 3 9 2 4 8 5 6
9 6 1 5 3 7 2 8 4
2 8 7 4 1 9 6 3 5
3 4 5 2 8 6 1 7 9
代码
#include<bits/stdc++.h>
using namespace std;
int a[20][20];//存储数独
int h[20][20], l[20][20], x[20][20]; //表示行,列,小方块内是否出现过1-9
//打表,通过坐标判断属于哪一个九宫格小方块
const int xiao[10][10] = {{0,0,0,0,0,0,0,0,0,0},
{0,1,1,1,2,2,2,3,3,3},
{0,1,1,1,2,2,2,3,3,3},
{0,1,1,1,2,2,2,3,3,3},
{0,4,4,4,5,5,5,6,6,6},
{0,4,4,4,5,5,5,6,6,6},
{0,4,4,4,5,5,5,6,6,6},
{0,7,7,7,8,8,8,9,9,9},
{0,7,7,7,8,8,8,9,9,9},
{0,7,7,7,8,8,8,9,9,9}};
//为了降低复杂度,只找需要填数的坐标
struct ty{
int x, y;
}kong[90];
int cnt = 0;
void write(){
for(int i = 1; i <= 9; i++){
for(int j = 1; j <= 9; j++){
cout << a[i][j] << " ";
}
cout << endl;
}
}
void dfs(int dep){
if(dep > cnt){
write();
return;
}
int xx = kong[dep].x;
int yy = kong[dep].y;
for(int i = 1; i <= 9; i++){
if(h[xx][i] == 0 && l[yy][i] == 0 && x[xiao[xx][yy]][i] == 0){//判断是否填过数
a[xx][yy] = i;
h[xx][i] = 1;//填过则标记为1
l[yy][i] = 1;
x[xiao[xx][yy]][i] = 1;
dfs(dep+1);
h[xx][i] = 0;//清零
l[yy][i] = 0;
x[xiao[xx][yy]][i] = 0;
}
}
}
int main() {
for(int i = 1; i <= 9; i++){
for(int j = 1; j <= 9; j++){
cin >> a[i][j];
if(a[i][j] == 0){//如果为0,说明需要填数
kong[++cnt].x = i;//用kong存放空(0)的坐标
kong[cnt].y = j;
}else{
h[i][a[i][j]] = 1;//否则标记为1,表示不需要填数
l[j][a[i][j]] = 1;
x[xiao[i][j]][a[i][j]] = 1;
}
}
}
dfs(1);
return 0;
}
例三:幸运数字
题目描述
定义一个数字为幸运数字当且仅当它的所有数位都是4或者7。
比如说,47、744、4都是幸运数字而5、17、467都不是。
定义next(x)为大于等于x的第一个幸运数字。给定l,r,请求出next(l) + next(l + 1) + ... + next(r - 1) + next(r)。
输入描述:
两个整数l和r (1 <= l <= r <= 1000,000,000)。
输出描述:
一个数字表示答案。
示例1
输入
2 7
输出
33
示例2
输入
7 7
输出
7
代码
queue
1.queue初始化
queue<Type, Container> (<数据类型,容器类型>)
初始化时必须要有数据类型,容器可省略,省略时则默认为deque 类型
2.queue常用函数
push() 在队尾插入一个元素
pop() 删除队列第一个元素
size() 返回队列中元素个数
empty() 如果队列空则返回true
front() 返回队列中的第一个元素
back() 返回队列中最后一个元素
memset用法详解
memset是一个初始化函数,作用是将某一块内存中的全部设置为指定的值。
void memset(void*s,int c, size_t n)
·s指向要填充的内存块
·c是要被设置的值
·n是要被设置该值的字符数
·返回类型是一个指向存储区s的指针
注意
1.不能任意赋值
memset函数是按照字节对内存块进行初始化,所以不能用它将int数组初始化为0和-1之外的其他值(除非该值高字节和低字节相同)。
其实被设置的值(即c)的实际范围应该在0~255,因为memset函数只能取c的后八位给所输入范围的每个字节。也就是说无论c多大只有后八位二进制是有效的
2.注意所要赋值的数组的元素类型
例一:对char类型的数组a初始化,设置元素全为'1'
#include <iostream>
#include <string.h>
using namespace std;
int main()
{
char a[4];
memset(a,'1',4);
for(int i=0;i<4;i++)
cout << a[i] << " ";
return 0;
}

例二:对int类型的数组a初始化,设置元素值全为1
#include <iostream>
#include <string.h>
using namespace std;
int main()
{
int a[4];
memset(a,1,sizeof(a));
for(int i=0;i<4;i++)
cout << a[i] << " ";
return 0;
}

首先数组a是int型的,占四个字节,所以在使用memset时
memset(a,1,4);语句是错误的:memset是以字节为单位进行赋值的
所以正确的语句应该是memset(a,1,16);或者memset(a,1,sizeof(a));
但是输出的结果仍然不是全为1,为什么?
——回到上一点:memset是以字节为单位进行赋值的,所以将1(00000001)赋给每一个字节。那么对于a[0]来说,其值为(00000001 00000001 00000001 00000001),即十进制的16843009。
memset函数在初始化处理时非常方便,但也有其局限性,比如要注意初始化数值,要注意字节数等等。当然,直接选择用for循环或while循环来进行初始化也是可以的,只不过memset更快捷一些。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号