P2607 [ZJOI2008] 骑士

原本打算做出来之后在洛谷上面交的，然后一看已经满了，所以就在别的地方发表吧。

\(\tiny \text{打状态转移方程实在太辛苦了！！！}\)

题意：

给定一个无向基环树森林，点带点权，求其独立集的权值最大值。

为什么是无向基环树森林呢？因为一个骑士和他痛恨的骑士无论如何都不会一起被选上了，所以即使设前者也被后者痛恨也是没有影响的。

显然基环树之间是独立的，所以考虑在一棵基环树上面跑最大独立集。

很容易发现这道题的弱化版是 P1352 没有上司的舞会，大家可以先去做一下，这对独立思考此题至关重要。

---

好的，默认大家已经做完了。考虑从树上 dp 扩展到基环树上 dp。一般地，设深搜树上导致有环的那条回边为 \(up \to dn\)，其中 \(up\) 深度更低。

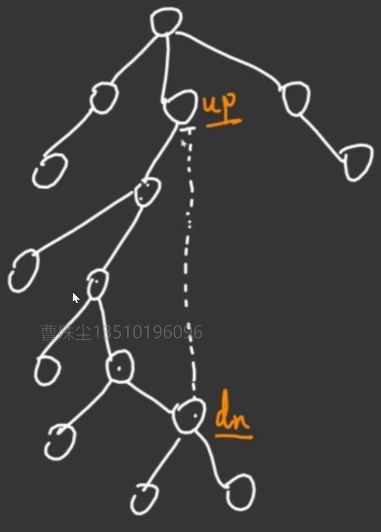
发现基环树只比普通的树上增加了一个额外的限制：\(up\) 和 \(dn\) 不能同时取。所以当我们计算 \(up\) 的 dp 值的时候，还需要考虑 \(dn\) 选了没选。

因为 \(dp\) 的状态制度是一直沿用的（也就是你一开始设了 dp[n][4] 以后也需要考虑其他点的 dp[n][4]），所以所有包含 \(dn\) 的子树需要同时记录 子树的根结点取不取 和 \(dn\) 结点取不取。

于是这个时候就得出来了 \(dp\) 的状态：

设 \(dp_{i,0}\) 和 \(dp_{i,1}\) 表示不取 \(dn\) 的情况下，\(i\) 取 / 不取的最大答案。

设 \(dp_{i,2}\) 和 \(dp_{i,3}\) 表示取 \(dn\) 的情况下，\(i\) 取 / 不取的最大答案。

这个状态的表示已经足够全面：因为基环树的独立集只比树上的独立集多了一个东西。

---

显然，有时候如果 \(i\) 不在环上，也不在 \(up\) 的祖先，即 \(i\) 的子树里面没有 \(dn\)，就需要进行一些初始化的约定（因为这个时候的 \(i\) 完全与多出来的限制无关，只需要求解两个状态就行了）：

这时候就设 \(dp_{i,1} = dp_{i,3}\)，以及 \(dp_{i,2} = dp_{i,0}\) 即可。

另外，还有一个情况，也就是 \(i=dn\) 的情况：显然这个时候 \(dp_{i,1}\) 和 \(dp_{i,2}\) 是完全无意义的，要设为负无穷大。

---

考虑推导转移方程。

显然，在一开始对于所有的 \(i\)，\(dp_{i,0} = dp_{i,2} = 0\)，\(dp_{i,1} = dp_{i,3} = val_i\)。其中 \(val_i\) 表示点权。

对于 \(i=dn\)，\(dp_{i,1} = dp_{i,2} = -\infty\)。

对于 \(i \not = dn,i \not = up\)，枚举其子结点 \(x\)（没有被访问过）：

• 不取环底，\(i\) 也不取：\(dp_{i,0}+\max(dp_{x,0},dp_{x,1}) \to dp_{i,0}\)。（自己都不取了，子结点取不取当然随意）

• 不取环底，\(i\) 取：\(dp_{i,1}+dp_{x,0} \to dp_{i,1}\)。（自己取了，子结点肯定不能取）

• 显然因为这个时候 \(i\) 和 \(dn\) 没有直接的联系，所以取环底和不取环底是一模一样的两种情况，即有：

  • \(dp_{i,2}+\max(dp_{x,2},dp_{x,3}) \to dp_{i,2}\)

  • \(dp_{i,3}+dp_{x,2} \to dp_{i,3}\)

对于 \(i = up\)，同样枚举其子结点 \(x\)（没有被访问过）：

• \(dp_{i,2} = dp_{i,3} = -\infty\)。

• \(dp_{i,0} + \max\{dp_{x,0},dp_{x,1},dp_{x,2},dp_{x,3}\} \to dp_{i,0}\)。

• \(dp_{i,1} + dp_{x,0} \to dp_{i,1}\)。

对于答案，其就是对于每一个基环树的根结点 \(i\)，计算 \(\max\{dp_{i,0},dp_{i,1},dp_{i,2},dp_{i,3}\}\) 即可。

#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N = 1000010;
int n;
int val[N];
vector<int> v[N];
int dp[N][4];
bool stk[N], vis[N];
int up;

void dfs(int u, int pre) {
	vis[u] = stk[u] = 1;
	dp[u][1] = dp[u][3] = val[u], dp[u][0] = dp[u][2] = 0;
	for (auto i : v[u])
		if (!vis[i]) {
			dfs(i, u);
			if (u == up) {
				dp[u][0] += max(max(dp[i][0], dp[i][1]), max(dp[i][2], dp[i][3]));
				dp[u][1] += dp[i][0];
				dp[u][2] = dp[u][3] = -1e16;
			} else {
				dp[u][0] += max(dp[i][0], dp[i][1]);
				dp[u][1] += dp[i][0];
				dp[u][2] += max(dp[i][2], dp[i][3]);
				dp[u][3] += dp[i][2];
			}
		} else if (i != pre && stk[i])
			up = i, dp[u][1] = dp[u][2] = -1e16;
	stk[u] = 0;
}

signed main() {
	cin >> n;
	for (int i = 1; i <= n; i++) {
		int x;
		cin >> val[i] >> x;
		v[i].push_back(x), v[x].push_back(i);
	}
	int ans = 0;
	for (int i = 1; i <= n; i++)
		if (!vis[i])
			up = 0, dfs(i, 0), ans += max(max(dp[i][0], dp[i][1]), max(dp[i][2], dp[i][3]));
	cout << ans << endl;
	return 0;
}

一道蓝题做这么久，身败名裂！！！