进阶 DFS 学习笔记

文章盗的图注明了出处，全部出自 y 总的算法提高课。

不知道为啥这个时候才开始学这个东西，好像是很多同龄人都已经学完了。

进阶 DFS 具体来说好几个东西，所以可能内容有一些些多。

默认 DFS 和 BFS 已经掌握了，且对最短路有了解，而且知道 DFS 该如何剪枝。否则建议出门左转。

直接进入正题。

双向广搜

BFS 显然没有 DFS 那么多变（DFS 可以大力剪枝），但是也是有一些优化方法的。

其中比较常用的，就是双向广搜，和 A-star 算法这两个东西，其中 A-star 也可以被称作 A*。

首先来讲双向广搜。

先剧透一下：双向广搜的名字很好理解，但是使用场景有一个约束：最终需要到达的状态必须不能很多。

双向广搜可以把时间复杂度弄到大约是开根号的一个级别。

双向广搜顾名思义啊，就是从两个方向同时进行广搜，而不是从一个方向搜到另外一个方向。

双向广搜实际上和 Meet-in-the-middle 是两个差不多的东西。只不过前者是双向的 BFS，后者可以是双向的 DFS 也可以是双向的 BFS。

为什么要这么做呢？因为有些 BFS 的状态可能会多到爆炸，连 \(O(n)\) 的算法也无法治疗。

例如经典的八数码问题，一共是 \(9\) 个格子，那么就是 \(9!\) 级别的状态，有一些大，但是还是可以治疗一下。

但是如果扩展到十五数码问题，一共是 \(15\) 个格子，那么就直接废了。

例如 Acwing 190. 字串变换这道题，显然可以想到使用 BFS 来跑，对于每一个状态向可以到达的状态连一条边。但是每一个字符串的长度最多有 \(20\) 个（相对于来讲有些巨多），而规则一共只有 \(6\) 个，而我们只需要搜 \(10\) 步。

显然可以算出来这里的状态数量为 \(6^{10}\) 个，时间和空间都不太吃得消。

所以要优化。

优化的这个时候就有了一个很常用的方式：从起点和终点同时开始搜，这样就可以得出双向广搜。

就有点像走迷宫的时候，有时候采用一边从起点走迷宫，一边从终点逆推的方法会快一些。

考虑到每一层的状态数都是成指数增加的，但是，发现字串变换那道题，最终达到的状态需要考虑的只有一个！

偷一张 y 总的图：

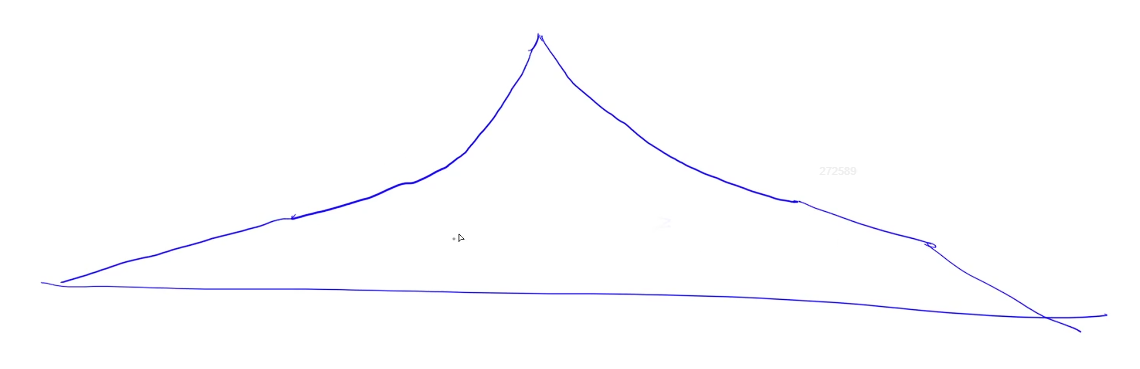
最上面的那个点就是起点，而每一次的状态都在疯狂增加，最终会形成一个宽边帽的形式。

但是，如果从终点同时往回搜，就会成为这个样子：

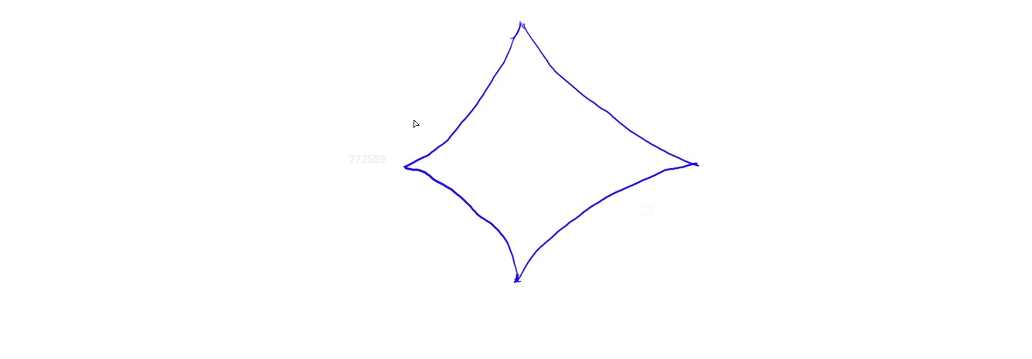
显然，面积小了很多！！对应的，状态数量也小了很多！

而且在搜到中间层的时候，就会相遇了。字串变换的那道题很友好地告诉我们：我们只需要搜 \(10\) 步即可。所以如果从起点和终点共同出发，相遇的地方就是两者都走了 \(5\) 步的时候，也就是对应 \(6^5 \times 2\)，整整把复杂度开了个平方！

但是考虑如何判断相遇的时候，可以直接使用 map 往上莽即可，看一下对于一个状态在对面有没有相同的状态。最终还会多一个 \(\log\) 但是无伤大雅。可见双向广搜的优化效果是很优秀的。

于是这道题就做完了，双向广搜也就同时讲完了。

最终还有一些尾巴，也就是双向广搜的一个小优化。

首先有一个不那么聪明的做法，就是直接先跑完两边的，或者是左边扩展一步，再右边扩展一步。

但是还有一点优化常数的做法。为了节省时间，我们可以在每一次需要扩展的时候看一下是左边的队列元素少还是右边的队列元素少。

可以感性理解，想想为什么。

#include <bits/stdc++.h>
using namespace std;
typedef unordered_map<string, int> um;//使用 typedef 来简化代码
string s, t;
string a[10], b[10];
int n = 1;

int ex(queue<string> &q, um &mp1, um &mp2, string a[], string b[]) {//扩展
	string t = q.front();
	q.pop();
	for (int i = 1; i <= n; i++)
		for (int j = 0; j + a[i].size() <= t.size(); j++)
			if (t.substr(j, a[i].size()) == a[i]) {//找有没有可以替换的地方
				string to = t.substr(0, j) + b[i] + t.substr(j + a[i].size());
				if (mp2.count(to))
					return mp1[t] + mp2[to] + 1;
				if (mp1.count(to))
					continue;
				q.push(to), mp1[to] = mp1[t] + 1;
			}
	return 11;//没有找到
}

int bfs(string s, string t) {
	queue<string> q1, q2;
	um mp1, mp2;
	q1.push(s), q2.push(t);
	mp1[s] = 0, mp2[t] = 0;
	while (!q1.empty() && !q2.empty()) {
		int x;
		if (q1.size() <= q2.size())
			x = ex(q1, mp1, mp2, a, b);
		else
			x = ex(q2, mp2, mp1, b, a);
		if (x <= 10)//找到答案直接返回
			return x;
	}
	return 11;
}

int main() {
	cin >> s >> t;
	while ((cin >> a[n] >> b[n]))
		n++;
	n--;
	if (s == t) {//特判！！
		cout << "0\n";
		return 0;
	}
	int x = bfs(s, t);
	if (x <= 10)
		cout << x << endl;
	else
		cout << "NO ANSWER!";
	return 0;
}

代码跑得飞快，即使在 Acwing 老爷机的情况下也跑了 20ms。可见其优化效果显著。

A-star 算法

我们也将迎来第一个重头戏。

这个名字非常高级，把一个优化 BFS 的名字写得冠冕堂皇，我也不知道为什么，但是这个算法是真的有点用。

这个算法需要改进的 BFS 的不足，和双向 BFS 改进的一样。都是在浩瀚如海的状态下找到一个状态到另一个状态的最短路径。

不过 A-star 算法和双向广搜的处理方法不同，A-star 算法在原有 BFS 的基础下加了一个启发函数（人类智慧）。~~梦回启发式合并~~

那么这个启发函数是干嘛的呢？大家先不用管这个东西是什么，先想想这个东西要有什么作用。

实际上这个东西的作用是这样的：充分发扬人类智慧，得出启发函数，使得起点只需要走很少个点就可以搜到终点。上面这句话也可以说是 A-star 算法的核心思想。

A-star 算法的使用场景：状态很多，而且状态之间的边权可以为负数，但是不能出现负环。

我们来了解一下算法的流程。

首先，我们会将 BFS 中的队列换成优先队列。队列是小根堆。每一个元素包含两个要素：一个是从起点到当前点的真实距离，一个是从当前点到终点的估价距离。

（众所周知，当看到“估价”的字眼的时候，我们就已经猜到这个东西是人类智慧了。）

而且还有一个更加奇怪的点：优先队列按照真实距离和估价距离的和来排序（其实很好理解，就是估计的起点到终点的距离，但是这个不确定性实在是有点无法忍受）。这是什么玩意？

然后就是比较容易理解的部分：对于每一条路径，挑一个和最小的点来扩展。这也是为什么这个东西是小根堆。

注意，A-star 算法不需要在搜索的时候判重。

当发现终点出队的时候，没错，这个和就是答案。

其实我上面讲的 A-star 算法的使用场景的内容还漏掉了一个点：A-star 算法不一定什么时候都是正确的。

实际上有一个结论：只要对于每一个状态状态到终点的估价函数都 \(\le\) 状态到终点的实际距离，而且每一个估价函数都必须要非负数（否则错得更加离谱），A-star 算法就是正确的。

（再插叙一条对下面的内容有帮助的结论：状态到终点估价函数和实际距离越接近越好，显然估价函数可以取 \(0\) 但是这样就退化为 dijkstra 算法了。）

考虑如何证明。考虑使用反证法：如果满足对于每一个状态状态到终点的估价函数都 \(\le\) 状态到终点的实际距离，但是终点第一次出队时得到的答案并不是最优的。

接下来找矛盾点即可。

设终点为 \(T\)，起点为 \(S\)。

记 \(f_x\) 表示状态为 \(x\) 的时候 \(x \to T\) 的估价函数，\(g_x\) 表示状态为 \(x\) 的时候 \(x \to T\) 实际距离，\(d_x\) 表示起点 \(S \to x\) 的实际距离，而 \(ans_x\) 表示 \(d_x + f_x\)。显然 \(f_x \le g_x\)，而且优先队列是按照 \(ans_x\) 来排序的。

设终点 \(T\) 时算出起点到 \(T\) 的距离时 \(ans_T=d_T\)，而应该算出来的答案为 \(d_{最优} = ans_{最优}\)。显然 \(d_T > d_{最优}\)。设这个最优答案属于的点为 \(u\)。

则 \(d_u + f_u \le d_u + g_u = d_{最优}\)，可以得出 \(d_T > d_{最优} \ge d_u + f_u = ans_u\)，于是，观察式子可以发现 \(ans_T > ans_u\)，那么并不应该是 \(T\) 为第一个终点出队的点啊！而是 \(u\)！

找到了矛盾点。所以得证这个结论是正确的。

注意，A-star 算法只能求出全局最小值，并不能求出局部最小值。这点需要特别注意。~~话说这东西思想没啥却咋这么多规矩~~

很容易找到一个反例：

~~欸，我再盗一张图：~~

注意看一下中间的那个交点，其如果是正常跑 A-star 的话它会从上面的一条路走过来，得到局部“最优解”是 \(6\)。但实际上它可以从下面的点走过来，这样的答案原本是 \(<6\) 的。所以这个东西不能求出局部最小值。

这也是《算法竞赛进阶指南》中写错的一个点。

估价函数还是 A-star 算法中比较重要的一个点，但是估价函数的优秀的构造方法一般都很人类智慧，很难自己想到。

所以我们只好借鉴前人的思想，因为 A-star 算法的题目实在不多，所以把每一种题型的估价函数构造方法都弄熟练即可。

当然如果你考试时遇到了你不会的模型，你只能听天由命，或者猜一个了。

这需要你的想象力。

Acwing 179. 八数码

我们来看一道 A-star 算法的练手题。

对于八数码问题有一个快速判断是否无解的充要条件：

如果将输入的序列里面去掉那个叫做 x 的项，如果这个序列的逆序对的数量是偶数则有解，否则无解。

这里就不证了，好像很难证。大约是和哈密顿回路有关系。

考虑找出估价函数。

不妨设估价函数为当前状态中每个数与它的目标位置的曼哈顿距离之和。

这是可能的最优情况（也就是每一轮都有一个数可以向目标位置移一格，显然这是最好的情况），可以证明不管实际情况的答案有多么优秀，一定都不小于这个值。

于是就这么简单地得出来了策略。

#include <bits/stdc++.h>
using namespace std;
const string fin = "12345678x";

int dx[] = {0, 1, 0, -1};

int dy[] = {1, 0, -1, 0};
string op = "rdlu";//操作，便于还原方案

inline int get(string s) {//估价函数
	int x = 0;
	for (int i = 0; i < 9; i++)
		if (s[i] != 'x') {
			int a = s[i] - '1';//注意这里是 1 而不是 0！！！笔者这里卡了好久！！警钟长鸣！
			x += abs(i / 3 - a / 3) + abs(i % 3 - a % 3);
		}
	return x;
}
typedef pair<int, string> pis;//简化一下代码
inline void bfs(string st) {
	unordered_map<string, int> dep;//每一个点的步数
	unordered_map<string, pair<string, char> > pre;//每一个点的前驱，用来还原方案
	priority_queue<pis, vector<pis>, greater<pis> > q;
	q.push({get(st), st});
	dep[st] = 0;
	while (!q.empty()) {//首先队列非空
		string st = q.top().second;
		q.pop();
		int dp = dep[st];
		if (st == fin)//碰到终点直接退出
			break;
		int px, py;
		for (int i = 0; i < 9; i++)
			if (st[i] == 'x')
				px = i / 3, py = i % 3;//找 'x' 的位置
		string nw = st;
		for (int i = 0; i < 4; i++) {//尝试移动 'x'
			int x = px + dx[i], y = py + dy[i];
			if (x < 0 || x > 2 || y < 0 || y > 2)
				continue;//判断是否越界
			swap(st[x * 3 + y], st[px * 3 + py]);//移动
			if (!dep.count(st) || dep[st] > dp + 1) {//首先如果没有被访问到肯定可以加入队列，其次如果被访问到了但是从这里走会更优也可以重新加入队列
				dep[st] = dp + 1;
				pre[st] = {nw, op[i]};//记录前驱
				q.push({dep[st] + get(st), st});//加入队列
			}
			swap(st[x * 3 + y], st[px * 3 + py]);//还原
		}
	}
	string nw = fin, opr;
	while (nw != st) {//找出方案
		opr += pre[nw].second;
		nw = pre[nw].first;
	}
	reverse(opr.begin(), opr.end());//这里需要反转一下，因为是倒着走的
	cout << opr << endl;
}

int main() {
	string s, x;
	char c;
	while (cin >> c) {//cin>>c 是一个友好的东西，可以帮我们过滤掉空格
		s += c;
		if (c != 'x')
			x += c;
	}
	int cnt = 0;
	for (int i = 0; i < 8; i++)
		for (int j = i + 1; j < 8; j++)
			cnt += (x[i] > x[j]);//算逆序对
	if (cnt & 1)//逆序对为奇数的时候则无解
		cout << "unsolvable";
	else
		bfs(s);
	return 0;
}

Acwing 178. 第 K 短路

感谢这篇博客把我一句话点醒了，大家快去点赞！

这句话就是：

我们知道在 BFS 中，第一次搜索到达终点的路径就是到终点的最短路，那么第 \(k\) 次到达终点的路径当然就是到终点的第 \(k\) 短路了。

~~我学了三年的算法竞赛怎么就没想到呢.jpg~~

而这里的 \(k \le 1000\)，允许我们一次一次地到达终点。

但是这里需要注意的是：因为允许多次访问一个点（终点就是一个例子），所以每一个点走相邻地点时，不能再像 dijkstra 一样看相邻的结点走过了就不走了，而是必须要走所有相邻的结点。

所以我们就有了暴力的做法，感觉这种方法的复杂度比较玄学，但是肯定不能过。

但是根据数学直觉发现状态数量会非常庞大（每一个点都会走 \(k\) 次左右），于是考虑 A-star 算法。

这里需要注意一个点，想到了就谈一下：这个时候 A-star 算法依旧不能求出局部最小值，所以也不能求出除了终点之外的点的第 \(k\) 短路径。

A-star 算法就只需要思考两个东西：无解情况 和 估价函数。

首先考虑估价函数。显然有一个可能的构造方法就是：每一个点的估价函数都是这个点到终点的最短路径。这是有一些显然的，这样一定是小于等于实际情况的。

显然可以通过建反边跑最短路来求估价函数。

考虑再把估价函数再放大一点（这样可以节省时间），但是现实已经不允许我们再优化了。例如如果 \(k=1\) 的话，对于某一些结点，它的估价函数就是恰好等于实际情况。所以这样是最大的可能的值。

考虑无解情况，就是当终点不能到达起点的时候显然不可以（路径的数量为 \(0\)）。剩下的无解情况就直接交给 A-star 算法看一下能不能熬到 \(k\) 次到达终点即可。

实际上也可以通过拓扑排序 + DAG 上 DP 来搞，这样就可以完全判断所有的无解情况，但是这样太复杂了。

代码有一点点难写。。

感觉搜索和 dp 在代码复杂度上面很像反义词。搜索是思路不难，但是代码并不好写。而 dp 是思路有些恶心，而代码相比搜索来说算短的（那些十几个转移方程和需要科技来优化的除外）。

但是这道题不需要上一道题一样使用 unordered_map 来记录每一个状态的步数了（这样有点难搞），直接加入状态。具体地，每一个状态记录：起点到这个点的距离和这个点的估价函数的和，起点到这个点的距离和这个点的编号。

这道题有一些些坑，在代码里面会体现出来。

#include <bits/stdc++.h>
#define int long long
using namespace std;
int n, m;
const int N = 1010;
int f[N];
bool vis[N];
int s, t, k;
typedef pair<int, int> pii;
typedef pair<int, pii> piii;
vector<pii> v[N], fv[N];

void dijkstra(int s) {
	for (int i = 1; i <= n; i++)
		f[i] = 1e15;
	f[s] = 0;
	priority_queue<pii, vector<pii>, greater<pii> > q;
	q.push({0, s});
	while (!q.empty()) {
		int u = q.top().second;
		q.pop();
		if (!vis[u])
			vis[u] = 1;
		else
			continue;
		for (auto [to, w] : fv[u])
			if (f[to] > f[u] + w && !vis[to]) {
				f[to] = f[u] + w;
				q.push({f[to], to});
			}
	}
}
int cnt[N];

int bfs() {
	priority_queue<piii, vector<piii>, greater<piii> > q;
	q.push({f[s], {0, s}});
	while (!q.empty()) {
		int u = q.top().second.second, dis = q.top().second.first;
		q.pop();
		cnt[u]++;
		if (cnt[t] == k)
			return dis;
		for (auto [to, w] : v[u])
			if (cnt[to] < k)//坑二，需要判断是否走了 <k 次，要不然就走了也没用
				q.push({dis + w + f[to], {dis + w, to}});
	}
	return -1;
}

signed main() {
	cin >> n >> m;
	for (int i = 1; i <= m; i++) {
		int x, y, w;
		cin >> x >> y >> w;
		v[x].push_back({y, w});
		fv[y].push_back({x, w});
	}
	cin >> s >> t >> k;
	if (s == t)//坑一
		k++;
	dijkstra(t);
	if (f[s] == 1e15) {
		cout << "-1\n";
		return 0;
	}
	cout << bfs() << endl;
	return 0;
}

迭代加深搜索

乍一看这些搜索名字好像都挺高级的，实际上并不难。

迭代加深搜索的英文名是 IDDFS，也就是加上了 Iterative Deepening（迭代加深）的 DFS。

通过名字可以知道这是一种和深度有密切关系的 DFS 优化算法。

在搜索的时候，可能会有这样的情况发生：搜索树太高了，以至于每一次搜索一个分岔，返回都要很长时间。但是你要搜的答案在很浅层的位置。

而你如果按照普通的 DFS 来跑的话，你就需要在很多地方白跑一趟那么长的距离。然后你又发现你的答案不需要你跑那么远，好长的一段时间都白费了，就问你气不气？

但是，我们可以从搜索树的根结点开始，每一次迭代加深搜索树的深度，找这一层的结点里面是否有答案并计算答案。

显然，这样的效率会高很多。因为你找到答案你就直接输出了，没有必要再到所有更深的深度的结点里面里面去搜。

于是 IDDFS 的思想就是那么简单。

显然 IDDFS 不会劣于暴力 DFS，因为 DFS 遍历到的状态 IDDFS 最多也只会遍历到一次，而 DFS 没有遍历到的状态 IDDFS 就更不可能遍历到了。

然后就有人会问了：那这不是和 BFS 一模一样的吗，都是逐渐增加深度？

注意，BFS 的空间复杂度和迭代加深搜索不同。

BFS 的主体结构是一个队列，每一次访问一层也要记录下上一层的结点（这样的复杂度是指数级别的，比较浪费空间）。

而迭代加深搜索只会记录路径上的信息，所以它的时间空间复杂度是 \(O(n)\) 的（也就是和答案所在的深度成正比），比 BFS 更加优秀。

但是于是我们会发现迭代加深搜索有时候可能会比 BFS 更加优秀，但是 BFS 好写啊！

而且，迭代加深搜索相比于 BFS 有一个独门绝技。BFS 有 A-star 的优化算法，而迭代加深搜索有一个 IDA-star 算法，是前面的 A* 的优化版本。

可能有些人还会问：那么这个东西会不会效率太低呢？

等比数列求和公式告诉我们，这样的效率并不是太低的。

在最坏的情况下，设搜索树是二叉树，在第 \(n\) 层的点数为 \(2^n\)，而前 \(n-1\) 层的点数为 \(2^0+2^1 + \cdots + 2^{n-1} = 2^n - 1<2^n\)，发现前 \(n-1\) 层在最坏情况下相对于第 \(n\) 层单单一层的点数可以忽略不计！（算上的话也只是多了一个常数）。如果树的叉数更多，或者是情况不是最坏的，那就更可以忽略不计了！

那有些人就又会问：那么如果这个二叉树不是满二叉树呢？

不妨仔细思考一下。如果第 \(x\) 层相比于前 \(x-1\) 层的结点数并不多的话，那么这棵树就不是爆炸式增长的了，直接暴力也可以，何况 IDDFS 比暴力 DFS 更快呢。

所以这样优化是毋庸置疑的，很高效。想想你搜完前几层的 \(x\) 个点就搜到了答案就退出了，而普通的 DFS 必须要辛辛苦苦地全部搜一遍。

170. 加成序列

不妨来看一道 IDDFS 地练手题。

这道题要求我们构造一个数列满足题面中的要求，还要长度最小，且整个数列的值域 \(\le 100\)。

长度最小，就很容易想到使用 IDDFS 了。

其次，发现最终的答案可以是这样子的：\(1,2,4,8,16,32,64,128\)，可以发现长度为 \(8\) 的数列就已经可以使最后一个数 \(>100\) 了，所以可以证明最终的答案的长度不会大于 \(8\)。

于是就更加 IDDFS 了：答案的长度，也就是答案状态的深度不会超过 \(8\)。

显然可以加几个剪枝来优化一下时间：

剪枝一：优先枚举较大的数

这是显然的。这样可以尽可能地减小答案的长度。

剪枝二：排除等效的冗余

可能会有人不懂这是什么意思，实际上这个东西的含义很简单：就是排除相同的序列。

例如 \(1,2,3,4,\square\)，这个序列。很容易发现 \(\square\) 可以等于 \(1+4=2+3=5\)，所以这两种情况最终都会得出来一个相同的序列。

所以可以使用桶来搞。

剪枝三：使用性质

这个性质就是：每一个数至多是上一个数的两倍。

所以如果一个数即使每一次翻一倍都不能达到目标的话，那就直接 return 得了。

代码比较好写。就是直接枚举答案的长度，并 dfs 判断即可。

#include <bits/stdc++.h>
using namespace std;
const int N = 210;
int p[N];
int n;

bool dfs(int nw, int d) {
	if (nw > d)
		return 0;
	if (p[nw - 1] == n)//找到序列
		return 1;
	if (p[nw - 1] * (1 << (d - nw + 1)) < n)//剪枝三
		return 0;
	bool f[N] = {0};//初始化！！！
	for (int i = 0; i < nw; i++)
		for (int j = 0; j <= i; j++) {
			int sum = p[i] + p[j];
			if (sum > n || sum <= p[nw - 1]/*剪枝二*/ || f[sum])
				continue;
			f[sum] = 1, p[nw] = sum;
			if (dfs(nw + 1, d))
				return 1;
		}
	return 0;
}

int main() {
	p[0] = 1;
	while (1) {
		cin >> n;
		if (!n)
			return 0;
		int d = 1;
		while (!dfs(1, d))//迭代加深搜索
			d++;
		for (int i = 0; i < d; i++)//输出答案
			cout << p[i] << " ";
		cout << endl;
	}
	return 0;
}

IDA-star 算法

根据前面的 IDDFS 和 A-star 算法的启发，世界上诞生了一个叫做 IDA-star 算法，也就是迭代加深 A 星算法。

迭代加深只有在状态呈指数级增长时才有较好的效果，而 A* 就是为了防止状态呈指数级增长的，所以强强联手变成更强的东西。

众所周知 DFS 加上一个 ID 就可以优化很多，所以 A-star 加上一个 ID 也可以优化很多。这里的 ID 是一个很强的优化。

IDA-star 就是比较朴素的 dfs 加上一个估价函数，时间复杂度有些玄学，其他的和 A-star 算法没有啥共同点。

优化就是这个东西：

一开始先指定一个 \(d\)（要迭代加深的深度），然后就是一个非常强的剪枝：

如果一个点到答案的预估函数怎么样都会 \(>d\) 的话，那么就直接不搜这个点了。

这就是 IDA* 的思想。

180. 排书

显然每一次的决策可以有 \(\frac{15 \times 14 + 14\times 13 + 13\times 12 +\cdots + 2\times 1}{2} = 560\) 种，要爆搜的话显然最终的时间复杂度就是 \(O(560^4) = O(爆炸)\)。

但是显然可以使用双向广搜把它变成 \(O(560^2)\) 的，这样就可以过了。

考虑使用 IDA-star 来做这道题。

IDA-star 和 A-star 相同，还是需要思考如何设计估价函数。

显然最终排好序的序列一定是这样子的：\(1,2,3,\cdots,n\)。

考虑相邻两个元素之间的关系。显然，最终排好序的序列，后一个数的值是前一个数的值 \(+ \ 1\)。

考虑将 \([l,r]\) 从序列中删除，并移到另一个位置。再次将眼光放到相邻关系上面。发现最多会改变三个相邻关系。

所以，设要排序的序列是 \(a_1,a_2,a_3,\cdots,a_n\)，设 \(\sum_{i=1}^{n-1} (a_{i+1}-a_i \not = 1) = tot\)（也就是算相邻关系不对的数对数量），而每一次最多会纠正 \(3\) 个相邻关系。

所以最终一个序列的估价函数就是 \(\lceil \frac{tot}{3} \rceil = \lfloor \frac{tot+2}{3} \rfloor\)。可以证明，这是可能达到的最大值。

感觉这个思路太妙了，出题人真是个天才！！！

#include <bits/stdc++.h>
using namespace std;
const int N = 16;
int n;
int b[N], a[5][N];

int f() {//估价函数
	int res = 0;
	for (int i = 0; i < n - 1; i++)
		if (b[i + 1] != b[i] + 1)
			res++;
	return (res + 2) / 3;
}

bool get() {
	for (int i = 0; i < n; i++)
		if (b[i] != i + 1)
			return 0;
	return 1;
}

bool dfs(int d, int mx) {//直接大力 dfs
	if (d + f() > mx)
		return 0;
	if (get())
		return 1;
	for (int l = 0; l < n; l++)
		for (int r = l; r < n; r++)
			for (int k = r + 1; k < n; k++) {
				memcpy(a[d], b, sizeof b);
				int x, y;
				for (x = r + 1, y = l; x <= k; x++, y++)
					b[y] = a[d][x];
				for (x = l; x <= r; x++, y++)
					b[y] = a[d][x];
				if (dfs(d + 1, mx))
					return 1;
				memcpy(b, a[d], sizeof b);
			}
	return 0;
}

int main() {
	int T;
	cin >> T;
	while (T--) {
		cin >> n;
		for (int i = 0; i < n; i++)
			cin >> b[i];
		int d = 0;
		while (d < 5 && !dfs(0, d))
			d++;
		if (d >= 5)
			cout << "5 or more" << endl;
		else
			cout << d << endl;
	}
	return 0;
}

posted @ 2025-05-09 15:27 wusixuan 阅读(46) 评论(0) 收藏举报

刷新页面返回顶部

wusixuan