启发式合并学习笔记
以“启发式”来命名的算法有很多,有进阶搜索——启发式搜索,还有一个东西叫做启发式合并,还有一个是树上启发式合并,这两个东西这篇文章都会讲。
引用一句 OIwiki 上面的话:
启发式算法是基于人类的经验和直观感觉,对一些算法的优化。
简称人类智慧乱搞。
启发式合并
其实启发式合并我们以前就学过:在并查集里面有一个叫做启发式合并的 trick,配合并查集的路径压缩就可以把并查集进一步地优化到单次 \(O(1)\) 的级别。因为我们如果只是写路径压缩,那么这个时候并查集的合并就是无脑的,很慢。于是就有人有了灵感:能不能通过交换把小的集合合并到大的集合呢???于是,这个灵感就变成了“启发式”,加上合并就变成了“启发式合并”。
其实,广义的启发式合并就是同一个数据结构之间的合并。例如并查集合并、线段树合并……
其实他们最终的目标都是一个很简单的东西:set 合并。
我们来看一个引入题目,也是某一次 ABC 的 E 题的弱化版,当时那道 E 题还要维护前 \(k\) 大来着。当时我场切了,但是有很多不会启发式合并这个 trick 的人就做不出来了……
引入:有 \(n\) 个集合,每一个集合一开始只有 \(1\) 个元素,每一次按要求合并两个指定的集合。每一次都会有一个问题,所以你必须要真的维护。\(n \le 10^5,k \le 10\),时限 1s。
显然这里的 \(k\) 可以忽略,因为据笔者所知这道题的最优复杂度为 \(O(n \log^2 n)\),但是一共只会有 \(n-1\) 次合并,每一次可以暴力第 \(k\) 小所以复杂度为 \(O(nk)\)。相比之下显然可以忽略不计。
首先会有 \(O(n^2 \log n)\) 的暴力方式,可以证明这样可以跑满。显然这个时候是不行的。
但是!我们发现当复杂度的时候为 \(O(n \log^2 n)\) 的时候是可以通过的,因为 set 插入一定是需要 \(O(\log n)\) 的,所以我们只能把移动每一个元素的时间复杂度限制在 \(O(n \log n)\) 的范围内。
考虑使用启发式合并。
我们看一下到底是什么样的神仙数据能把暴力算法卡到 \(O(n^2 \log n)\),显然容易地可以构造:对于 \(1\le i \le n-1\),每一次把第 \(i\) 个集合合并到第 \(i+1\) 个集合那边去。每一次合并,\(i\) 的规模都恰好是 \(i\),于是会达到 \(1+2+\cdots+n = O(n^2)\) 个元素移动次数。
我们着眼于每一次第 \(i+1\) 个集合的规模,发现每一次第 \(i+1\) 个集合的规模只有 \(1\)!如果把第 \(i\) 移动到 \(i+1\) 会花费很多开销,那不妨就根据加法交换律,让 \(i+1\) 反主为客,直接把第 \(i+1\) 个集合合并到第 \(i\) 个集合上面去得了!
于是我们可以得到和并查集的启发式合并有着异曲同工之妙的合并方法:每一次把小集合合并到大集合。
那么这个东西的移动元素的复杂度为什么是 \(O(n \log n)\) 呢?
我们考虑在小集合的规模上面找突破口:因为大集合的规模 \(\ge\) 小集合的规模,所以 合并之后的规模 = 大集合的规模 + 小集合的规模 \(\ge\) \(2 \ \times\) 小集合的规模。
所以,小集合每一次合并之后的规模都会至少翻倍,也就是最多 \(\log n\) 次合并。
再着眼于小集合的元素上面,一个集合最多合并到其他集合 \(\log n\) 次,而这个集合的规模又不可能超过 \(n\)。所以如果要算元素合并的时间复杂度就是两个东西相乘,得到 \(O(n \log n)\)。显然这个东西是跑不满的,因为一个集合不一定一直都是“小集合”。
原题:ABC372E。
贴一下代码,引入题的每一个集合其实上就是并查集上面的集合。使用并查集和启发式合并维护即可。
#include <bits/stdc++.h>
using namespace std;
const int N = 200010;
struct number {
int num;
bool operator <(const number &a) const {
return num > a.num;
}
};
set<number> st[N];
int fa[N];
int n, m;
int find(int x) {
if (fa[x] == x)
return x;
return fa[x] = find(fa[x]);
}
void merge(int x, int y) {
x = find(x), y = find(y);
if (x == y)
return ;
if (st[x].size() > st[y].size())
swap(x, y);
fa[x] = y;
for (auto i : st[x])
st[y].insert({i});
st[x].clear();
}
int main() {
cin >> n >> m;
for (int i = 1; i <= n; i++)
fa[i] = i, st[i].insert({i});
while (m--) {
int op, u, v;
cin >> op >> u >> v;
if (op == 1)
merge(u, v);
else {
u = find(u);
if ((int)st[u].size() < v)
cout << "-1\n";
else {
int cnt = 0;
for (auto i : st[u]) {
cnt++;
if (cnt == v) {
cout << i.num << endl;
break;
}
}
}
}
}
return 0;
}
所以启发式合并的这个结论就是每一次把小的合并到大的,这个有点像贪心策略,就是证明有一点点奇怪。这个思想不仅在 set 上面体现了,还在其他数据结构上面有体现。
树上启发式合并(dsu on tree)
我们要迎来我们的重头戏了!!!坐稳了!!!
树上启发式合并,顾名思义,就是在树上进行一种启发式合并。
一般地,我们再来看一个引入题。
给一棵根为 \(1\) 的树,每一个点都有一个颜色,每一次询问子树颜色的种类数。
原题 https://www.luogu.com.cn/problem/U41492 。
显然这个题目我们不会选择在线询问,而是在询问之前先得出来所有的答案,然后再到时候直接查表即可。
先从石教练的板书上面盗一个图:
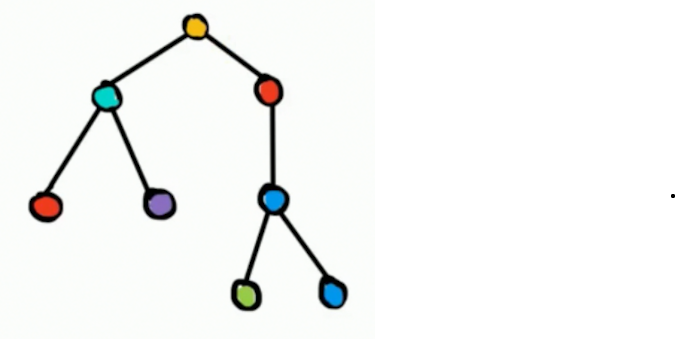
假设我们有这样的一棵树。
首先我们显然可以使用 dfs 暴力。复杂度是 \(O(n^2)\) 的,因为我们可以使用桶来记录。
但是这样还是太慢了,考虑优化。
看到树,你想到了什么???没错,树形 dp。
考虑对于每一个点记录其子树内所有颜色是否出现了。
注意:bitset 是不可行的,因为 \(O(\frac{n^2}{w})\) 的空间复杂度是不可以接受的,如果可以的话当我没说。
于是可以记录每一个点的子树内出现了多少种颜色,存在 set 里面,可以直接合并。
例如这样:
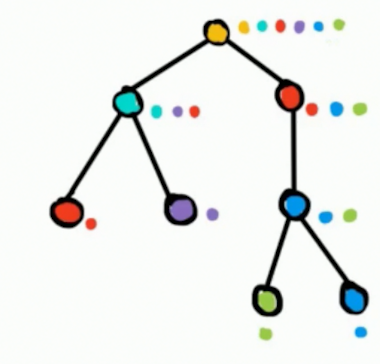
这个时候我们就可以得到一个 \(O(n \log^2 n)\) 的一个东西。但是空间会炸,还是需要优化。
注意,这个东西并不能叫做树上启发式合并。你可以直接叫他启发式合并优化树形 dp 得了,但是树上启发式合并并不是那么的简单(要么为啥还是今天的重头戏呢!)
实际上还有更加优美的做法。叫做 dsu on tree,也就是树上启发式合并,也有地方叫做静态链分治。
这个名字一看起来就很优美了。dsu 是并查集的意思,也象征着启发式合并,on tree 就是树上,合起来就是树上启发式合并。
它的时间复杂度是非常优秀的 \(O(n \log n)\),目前是这道题的最优做法。也是将要讲的重中之重。
看到“链”字你想到了什么?树链剖分好吧这确实有一点太牵强了。实际上,静态链分治和树链剖分确实有着一些共同点,比如都使用了重儿子的概念。
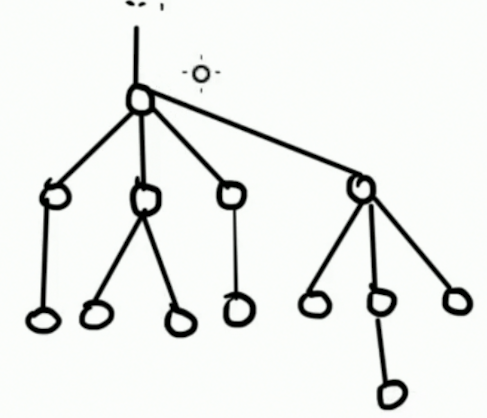
假设我们有这样的一棵树,略显庞大是不是。
这个时候如果要计算最上面的那一个点的答案,暴力做法就是需要遍历子树里面的所有点。这里假设把子树内的每一个点统计入答案的时间花销是 \(O(1)\)。因为某一些题目它真的不一定是 \(O(1)\) 的。因此暴力做法的时间复杂度就是 \(O(n)\) 的,显然不是很优秀。
那么静态链分治的做法是怎样的呢?
首先,最上面的点有 \(4\) 个儿子是不是??于是:
准备工作:在所有的儿子里面找出来一个重儿子,也就是子结点的子树规模最大的儿子,如果有多个最大而且相同的则取任意一个。
这里的重儿子的选择是很有道理的,在以后算法复杂度中会体现出来,和树链剖分选重儿子的原因是差不多的。
是不是就有点树链剖分的味道了?这里的重儿子的定义在《树形数据结构学习笔记》里面也提到过,不过你并不需要事先了解树链剖分是个什么东西。因为教练是先上静态链分治再上树链剖分的。
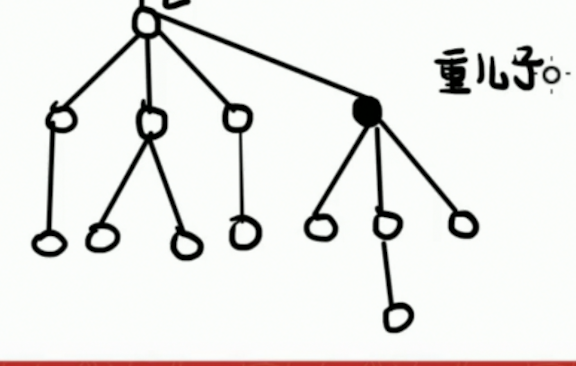
如图,被涂了实心的点就是重儿子。
这里定义不是重儿子的就是轻儿子。
不妨设在这个子树里面,最高点的编号为 \(u\),每一个颜色的出现次数为 \(cnt_x\) 表示第 \(x\) 个颜色的出现次数,\(ans_u\) 表示 \(u\) 这个结点的答案。
算法流程第一步:优先计算轻儿子的答案,对其进行内部统计并回答询问,回溯之后删除对 \(cnt\) 数组的影响,但是更新 \(ans_u\)。
算法流程第二步:然后再计算重儿子的答案,对其进行内部统计并回答询问,要保留重儿子对 \(cnt\) 的影响。
算法流程第三步:重新利用重儿子的信息来一次考虑 \(u\) 和轻儿子们,得到最终的 \(ans_u\)。
这东西乍一看就有点偷懒的感觉了,本质上没有改变多少,但是它的时间复杂度却似乎产生了很大的变化。还以为静态链分治是什么很牛的科技呢呃呃呃。
这实际上就是把轻儿子的子树遍历了两遍,把重儿子的子树遍历了一遍。这时候就有了选用重儿子的一大好处:可以通过偷懒来减少时间。
那凭什么这东西是 \(O(n \log n)\) 呢?
首先,我们需要请出一个 very familiar 的结论:对于每一个结点而言,它到根结点的路径上,轻儿子的数量最多有 \(\log n\) 个。
是不是和树链剖分一模一样的结论???
为了便于不影响不会树链剖分的选手的观感,我还是不厌其烦的口胡证明一下吧。
显然,当轻儿子到父亲结点的时候,子树规模一定 \(\times\) \(2\)。因为任意一个轻儿子的子树规模都一定不大于重儿子的子树规模。
而子树规模最多到 \(n\),而又每一次都 \(\times \ 2\),显然是 \(\log n\) 的量级。
所以这个结论就可以被证明了。
有了这个结论,我们就可以证明整个算法的复杂度是 \(O(n \log n)\)。
因为无论是轻儿子还是重儿子其子树里面所有的结点都至少要被算一次,并不能根据这个看出来轻儿子和重儿子又什么不同,所以是可以忽略的。
考虑着眼于轻儿子的子树被多遍历的那一次。
显然,对于每一个结点和它的某一个轻儿子祖先,这个结点一定会被多算一遍。因为这个结点一定在它祖先的子树里面,而这个祖先又是轻儿子,整个子树都需要多算。
但是根据上面给出的结论,每一个结点都至多有 \(\log n\) 个轻儿子祖先。而又有 \(n\) 个结点。
合起来就可以得到 \(O(n \log n)\) 的复杂度。时间复杂度得证。
静态链分治代码
这个东西确实有点人类智慧了,成功地把轻儿子和重儿子的独特性质发扬光大。
这个时候我们又遇到一个严峻的问题:那么这个东西该怎么写呢???
我们可以使用 dfs 序来维护一个子树里面的所有结点,显然可以证明一个子树内的 dfs 序是连续的。
int n,m,x,y,siz[N],son[N],lpos[N],rpos[N],id[N],val[N],ans[N],cnt,dfn;
vector<int> edge[N];
void dfs1(int u, int pre) {//有一点点像树链剖分的 dfs1
lpos[u] = ++dfn;//记录dfs序
id[dfn] = u;//dfs序上每一个下标对应的结点编号
siz[u] = 1;//子树规模
for (auto v : edge[u])
if (v != pre) {
dfs1(v, u);
siz[u] += siz[v];//更新子树规模
if (siz[v] > siz[son[u]])
son[u] = v;//更新重儿子
}
rpos[u] = dfn;//记录dfs序
}
void add(int x) {/*数据加入,自行设计*/}
void del(int x) {/*数据删除,自行设计*/}
void dfs2(int u, int pre, bool keep) {
for (auto v : edge[u])
if (v != son[u] && v != pre)
dfs2(v, u, false); //求轻儿子
if (son[u] > 0)
dfs2(son[u], u, true); //求重儿子
add(val[u]);
for (auto v : edge[u])
if (v != son[u] && v != pre) //轻儿子
for (int i = lpos[v]; i <= rpos[v]; ++i)
add(val[id[i]]);
//利用重儿子结果 + 轻儿子 + 本身 维护当前子树
ans[u] = ???; //记录答案
if (keep == false)
for (int i = lpos[u]; i <= rpos[u]; ++i)
del(val[id[i]]);//清空
}
void work() {
dfs1(1, 0);
dfs2(1, 0, false);
}
P3201 [HNOI2009] 梦幻布丁
这道题就是启发式合并的简单运用题目了。我也不知道为什么要评紫题。
直接维护即可。代码很短!
#include <bits/stdc++.h>
using namespace std;
int n, m;
const int N = 1000010;
set<int> st[N];
int a[N];
int main() {
cin >> n >> m;
for (int i = 1; i <= n; i++)
cin >> a[i], st[a[i]].insert(i);
int ans = 1;
for (int i = 1; i < n; i++)
ans += (a[i] != a[i + 1]);
while (m--) {
int op;
cin >> op;
if (op == 1) {
int x, y;
cin >> x >> y;
if (x == y)
continue;
if (st[x].size() > st[y].size())
swap(st[x], st[y]);
for (auto i : st[x])
ans -= (st[y].count(i - 1)) + (st[y].count(i + 1));//维护
for (auto i : st[x])
st[y].insert(i);
st[x].clear();
} else
cout << ans << endl;
}
return 0;
}
U41492 树上数颜色
作为静态链分治的引入题,我还是补一下 std 吧。
cnt 使用桶维护即可,其它的就都是板子。
#include <bits/stdc++.h>
using namespace std;
const int N = 100010;
int n;
int siz[N], son[N];
int l[N], r[N], id[N];
int a[N], ans[N], cnt, dfn;
int sum[N];
vector<int> v[N];
void dfs1(int u, int pre) {
l[u] = ++dfn;
id[dfn] = u;
siz[u] = 1;
for (auto i : v[u])
if (i != pre) {
dfs1(i, u);
siz[u] += siz[i];
if (siz[i] > siz[son[u]])
son[u] = i;
}
r[u] = dfn;
}
void add(int x) {
sum[x]++;
if (sum[x] == 1)
cnt++;
}
void del(int x) {
sum[x]--;
if (!sum[x])
cnt--;
}
void dfs2(int u, int pre, bool f) {
for (auto i : v[u])
if (i != son[u] && i != pre)
dfs2(i, u, 0);
if (son[u] > 0)
dfs2(son[u], u, 1);
add(a[u]);
for (auto i : v[u])
if (i != son[u] && i != pre)
for (int x = l[i]; x <= r[i]; x++)
add(a[id[x]]);
ans[u] = cnt;
if (f == 0)
for (int i = l[u]; i <= r[u]; i++)
del(a[id[i]]);
}
int main() {
cin >> n;
for (int i = 1; i < n; i++) {
int x, y;
cin >> x >> y;
v[x].push_back(y);
v[y].push_back(x);
}
for (int i = 1; i <= n; i++)
cin >> a[i];
dfs1(1, 0);
dfs2(1, 0, 0);
int m;
cin >> m;
while (m--) {
int x;
cin >> x;
cout << ans[x] << endl;
}
return 0;
}
CF1899G Unusual Entertainment
这道题叫你回答一个子树里面的某一些信息,很显然就可以想到树上启发式合并。
但是这里的树上启发式合并可能会有一些难写,好像还需要树状数组,一个 log 直接变成了两个 log,和不优化的 set 直接合并一样。所以这里不采用。
直接使用 set 直接合并子树里面的信息。
虽然 \(p\) 的值不是连续的,但是 \(p\) 的下标是连续的!!!所以就考虑把每一个点在 \(p\) 里面的位置当成 set 合并的筹码。
无法在线回答怎么办???那就离线回答:把每一个点的查询到保存下来。
还有一个细节,写在代码注释里面了。
#include <bits/stdc++.h>
using namespace std;
int t;
int n, q;
const int N = 100010;
vector<int> v[N];
set<int> st[N];
struct qry {
int l, r, id;
};
vector<qry> a[N];
bool ans[N];
void dfs(int u, int pre) {
for (auto i : v[u]) {
if (i == pre)
continue;
dfs(i, u);
if (st[i].size() > st[u].size())
swap(st[i], st[u]);
for (auto x : st[i])
st[u].insert(x);
}
for (auto [l, r, id] : a[u])
ans[id] = (st[u].lower_bound(l) != st[u].end()) && ((*st[u].lower_bound(l)) <= r);
//注意,这里不仅需要判断第二个条件,还要判断第一个。因为 *st[u].end() 的值可能是一个很魔怔的数,甚至可能会产生越界之类的问题
}
int main() {
cin >> t;
while (t--) {
cin >> n >> q;
for (int i = 1; i <= n; i++)
v[i].clear(), a[i].clear(), st[i].clear();
for (int i = 1; i < n; i++) {
int x, y;
cin >> x >> y;
v[x].push_back(y);
v[y].push_back(x);
}
for (int i = 1; i <= n; i++) {
int x;
cin >> x;
st[x].insert(i);
}
for (int i = 1; i <= q; i++) {
int l, r, x;
cin >> l >> r >> x;
a[x].push_back({l, r, i});
}
dfs(1, 0);
for (int i = 1; i <= q; i++)
cout << (ans[i] == 1 ? "YES" : "NO") << endl;
cout << endl;
}
return 0;
}
CF600E Lomsat gelral
这道题直接使用线段树合并即可。可以看我前面提到的那篇文章以学习线段树合并的相关内容。
#include <bits/stdc++.h>
#define int long long
#define mid ((l + r) >> 1)
using namespace std;
const int N = 100010;
int n, c[N];
vector<int> edge[N];
struct node {
int sum, cnt;
};
struct SegTree {
int cnt, rt[N], lc[31 * N], rc[31 * N];
node val[31 * N];
node pushup(node x, node y) {
if (x.cnt > y.cnt)
return x;
else if (y.cnt > x.cnt)
return y;
else
return {x.sum + y.sum, x.cnt};
}
int modify(int x, int l, int r, int v) {
if (!x)
x = ++cnt, lc[x] = rc[x] = 0, val[x] = {0, 0};
if (l == r) {
val[x].cnt++, val[x].sum = v;
return x;
}
if (v <= mid)
lc[x] = modify(lc[x], l, mid, v);
else
rc[x] = modify(rc[x], mid + 1, r, v);
val[x] = pushup(val[lc[x]], val[rc[x]]);
return x;
}
int merge(int x, int y, int l, int r) {
if (!x || !y)
return x + y;
if (l == r) {
val[x].cnt += val[y].cnt;
return x;
}
lc[x] = merge(lc[x], lc[y], l, mid);
rc[x] = merge(rc[x], rc[y], mid + 1, r);
val[x] = pushup(val[lc[x]], val[rc[x]]);
return x;
}
} st;
int ans[N];
void dfs(int x, int pre) {
for (auto i : edge[x])
if (i != pre) {
dfs(i, x);
st.merge(st.rt[x], st.rt[i], 1, n);
}
ans[x] = st.val[st.rt[x]].sum;
}
signed main() {
cin >> n;
st.cnt = n;
for (int i = 1; i <= n; i++)
st.rt[i] = i, st.lc[i] = st.rc[i] = 0, st.val[i] = {0, 0};
for (int i = 1; i <= n; i++) {
cin >> c[i];
st.modify(st.rt[i], 1, n, c[i]);
}
for (int i = 1; i < n; i++) {
int x, y;
cin >> x >> y;
edge[x].push_back(y);
edge[y].push_back(x);
}
dfs(1, 0);
for (int i = 1; i <= n; i++)
cout << ans[i] << " ";
return 0;
}
CF375D Tree and Queries
直接使用一个 sum 维护每一个颜色的出现次数,使用 \(cnt_i\) 表示出现次数 \(\ge i\) 的个数即可。
离线处理即可。
#include <bits/stdc++.h>
using namespace std;
const int N = 100010;
int n, m;
int siz[N], son[N];
int l[N], r[N], id[N], dfn;
int a[N], ans[N];
int sum[N], cnt[N];
vector<int> v[N];
vector<pair<int, int> > q[N];
void dfs1(int u, int pre) {
l[u] = ++dfn;
id[dfn] = u, siz[u] = 1;
for (auto i : v[u])
if (i != pre) {
dfs1(i, u);
siz[u] += siz[i];
if (siz[i] > siz[son[u]])
son[u] = i;
}
r[u] = dfn;
}
void add(int x) {
sum[x]++, cnt[sum[x]]++;
}
void del(int x) {
cnt[sum[x]]--, sum[x]--;
}
void dfs2(int u, int pre, bool f) {
for (auto i : v[u])
if (i != son[u] && i != pre)
dfs2(i, u, 0);
if (son[u])
dfs2(son[u], u, 1);
add(a[u]);
for (auto i : v[u])
if (i != son[u] && i != pre)
for (int j = l[i]; j <= r[i]; j++)
add(a[id[j]]);//不要把j写成i了!!!
for (auto [k, id] : q[u])
ans[id] = cnt[k];
if (!f)
for (int i = l[u]; i <= r[u]; i++)
del(a[id[i]]);
}
int main() {
cin >> n >> m;
for (int i = 1; i <= n; i++)
cin >> a[i];
for (int i = 1; i < n; i++) {
int x, y;
cin >> x >> y;
v[x].push_back(y);
v[y].push_back(x);
}
for (int i = 1; i <= m; i++) {
int u, k;
cin >> u >> k;
q[u].push_back({k, i});
}
dfs1(1, 0);
dfs2(1, 0, 0);
for (int i = 1; i <= m; i++)
cout << ans[i] << endl;
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号