2-SAT学习笔记

2-SAT

2-SAT 是一种满足性问题，其中 SAT 代表 satisfiability。

也就是说有一些限制，需要构造出答案使得所有的限制都满足。可能无解。

结合一下生活情景，你是否在逻辑推理的时候遇到这种题：

有 A,B,C,D,E,F,G 七个人，每个人要么去吃饭，要么就不去。请根据一下限制判断每个人去不去：
B 去则 A 不去
C 必须去
D,E 恰好去一个
E,F,G 不能去两个

这是一种非常实用的问题了。

但是 2-SAT 问题在限制上还加了一个限制，就是每一个限制涉及到的对象至多有两个。（这也是 2-SAT 中 2 的来源）

然而，第四个限制涉及到了 \(3\) 个对象，所以第四个限制是不能用 2-SAT 来解决的。实际上，n-SAT（如法炮制）若 n \(\ge\) 3，则是 NP 问题（即没有任何多项式复杂度的解法）。

不妨对这种富有生活趣味的问题抽象化，变成市面上大多的解释：

对于逻辑变量 \(x_1,x_2,x_3,···,x_n\) （取值为 \(0\) false 或 \(1\) true），使得一系列至多二元的运算全为真。
求是否有一组取值，若有，找出一种。

---

问题理解完毕，我们试图着手解决这个问题。

考虑讲所有的限制关系建成一个图。

发现一个变量可以有两种取值（0，1），普通的图是无法解决的。而这时候就有两种方法来处理这种情况：

• 增加边的属性数量：将属性数量变为四个，显然这样无法接受：我们不会允许图增加一些无端的重边。

• 增加点的属性数量：将每一个点分拆成两个，分别记录两种取值。

于是 2-SAT 采用了第二种方法。

所以有了取值的辅助，我们就可以对每一条边都下一个定义：对于建图之后的每一条边 \(A \to B\) 都表示如果 \(A\) 为真，则 \(A\) 为真。

A 和 B 是两个表达式，都有 \(x\) 和 \(-x\) 两种选择。

然而，我们又可以把所有的限制全都转化为 如果 \(A\) 为真，则 \(B\) 为真 的形式。

考虑这个时候 scc 的意义是什么：一个 scc 里面的点要么全为真，要么全为假。

容易发现，根据对称性，如果 \(A\) 和 \(B\) 在同一个 scc 里面，则 \(反A\) 和 \(反B\) 也一定在同一个 scc 里面。

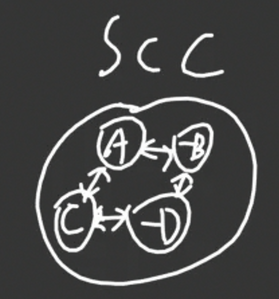
例如这个 scc。可以发现只要有一个结点为真，则一定可以通过传递的关系得到其他结点也是真（同真）。如果没有结点为真，那又变成同假。

所以可以得到无解的情况当且仅当是：如果 \(x\) 和 \(-x\) 在同一个 scc 里面，则一定无解。（因为他们本来就应该是相反关系，而在同一个 scc 里面又不得不同真同假）

再思考这个时候一条路径的意义是什么：

显然，如果 \(A\) 为真，则 \(B\) 为真，\(C\) 也为真。但是，当 \(A\) 为假，我们并不能知道 \(B\) 和 \(C\) 分别是什么。

因此，如果对于一个变量 \(x\)，存在 \(-x \to x\) 的一条路径。显然 \(-x\) 这个表达式不能为真（否则 \(x\) 也为真产生矛盾），所以可以得知 \(x\) 的表达式为真。

同理，如果对于一个变量 \(x\)，存在 \(x \to -x\) 的一条路径。显然 \(x\) 这个表达式不能为真（否则 \(-x\) 也为真产生矛盾），所以可以得知 \(x\) 为假。

如果 \(x \to -x\) 和 \(-x \to x\) 的两条路径同时存在，要不然就是无解了。

如果 \(x \to -x\) 和 \(-x \to x\) 的两条路径都不存在，那么 \(x\) 可以随便取。

---

假设我们已经判完了无解，而且已经将 scc 缩点。

设 \(-x\) 属于强连通分量 \(u\)，\(x\) 属于强连通分量 \(v\)。

那么难点在于确定 \(u \to v\) 和 \(v \to u\) 这两条路径究竟是否存在。

\(DAG\) 你想到了什么？没错拓扑排序。而且根据数学直觉，路径一定和拓扑序有关。

可以发现，如果上述路径存在，则一定可以通过拓扑序看出。

如果上述路径不存在，则也不可以通过拓扑序看出。例如：

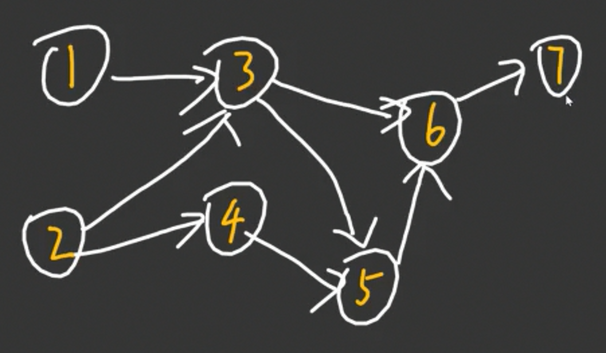
这里 \(1 \to 2\) 的路径不存在，但是不能通过拓扑序看出。但那又有什么关系呢！\(x\) 都随便取了，你说什么就是什么。我可以因为 \(2 > 1\) 说 \(x\) 为假，也可以说是真。

所以，我们只需要获取其拓扑排序编号，然后做比较即可。如果 \(id_v>id_u\)，则可以说 \(-x \to x\) 存在路径，\(x\) 为真。否则可以说 \(x\) 为假。

但是！拓扑排序编号，就是每一个点属于的强连通分量的编号。这里说的是栈的实现方式（使用 scc_cnt 对强连通分量编号），如果采用并查集的实现方式还是较麻烦了。

P4782 【模板】2-SAT

不妨来看一下模板题。

其实 2-SAT 的模板没有什么，前面都已经讲过，一个 tarjan 强连通分量，一个判断就行了。

不同的地方在于连边。

因为题目每一次给出了 "\(A\) 或 \(B\)" 这个约束条件，所以考虑建图。

如果 \(-A\)，则一定 \(B\)。如果 \(-B\)，则一定 \(A\)。于是可以连 \(-A \to B\) 和 \(-B \to A\) 两条边。

#include <bits/stdc++.h>
using namespace std;
const int N = 2000010;
int n, m;
vector<int> v[N];
int low[N], dfn[N], ind;
int color[N], scc_cnt;
stack<int> stk;

void tarjan(int u) {//tarjan 算法
	low[u] = dfn[u] = ++ind;
	stk.push(u);
	for (auto i : v[u]) {
		if (!dfn[i])
			tarjan(i), low[u] = min(low[u], low[i]);
		else if (!color[i])
			low[u] = min(low[u], dfn[i]);
	}
	if (low[u] == dfn[u]) {
		scc_cnt++;
		int x = 0;
		do {
			x = stk.top();
			stk.pop();
			color[x] = scc_cnt;
		} while (x != u);
	}
}

int main() {
	scanf("%d%d", &n, &m);
	while (m--) {
		int a, b, c, d;
		scanf("%d%d%d%d", &a, &b, &c, &d);
		v[a + b * n].push_back(c + (1 - d)*n);
		v[c + d * n].push_back(a + (1 - b)*n);//连边
	}
	for (int i = 1; i <= 2 * n; i++)
		if (!dfn[i])
			tarjan(i);
	for (int i = 1; i <= n; i++) {
		if (color[i] == color[i + n]) {
			printf("IMPOSSIBLE");
			return 0;
		}
	}
	printf("POSSIBLE\n");
	for (int i = 1; i <= n; i++)
		printf("%d ", (int)(color[i] < color[i + n]));
	return 0;
}

P3513 [POI 2011] KON-Conspiracy

给定一个无向图，要求将所有点划分为两个部分（间谍和后勤）。使得间谍的点集中没有边，后勤的点集的子图为完全图。

例如：

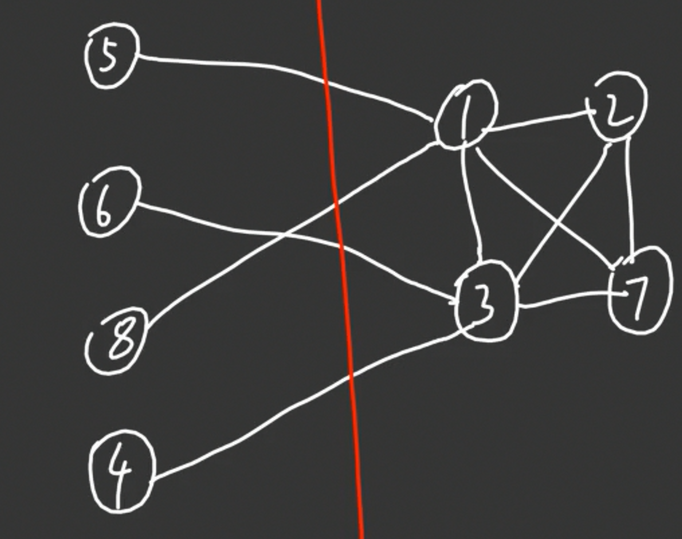
这是一种合理的划分策略。求有多少种合理的划分策略。

---

可以发现，每一个点确实只有两种情况：间谍和后勤二选一。对应着 2-SAT 中 0/1 的取值。不妨设当间谍为 \(1\)，做后勤为 \(0\)。

那么2-SAT 中的二元关系对应的什么呢？没错，可能你猜对了，就是每一条边。

假设 \(A,B\) 认识。

如果 \(A\) 当了间谍，则 \(B\) 不能当间谍。则连边 \(A \to -B\)，同理也可以反向连边 \(B \to -A\)。

但是如果 \(A\) 当了后勤，\(B\) 可以选当后勤也可以当间谍。所以这里是没有影响的。反过来同理。

假设 \(A,B\) 不认识。

如果 \(A\) 当了后勤，则 \(B\) 不能当后勤。则连边 \(-A \to B\)，同理也可以反向连边 \(-B \to A\)。

但是如果 \(A\) 当了间谍，\(B\) 可以选当后勤也可以当间谍。所以这里是没有影响的。反过来同理。

可以证明有且仅有这么多限制，建图跑 2-SAT，就可以得知一组可行解。复杂度 \(O(n^2)\)。

我们设这个通过 2-SAT 得出的可行解是第一组解。

注意，我们这里建图的唯一目的就是为了跑 2-SAT，这道题后面所说的所有有关图的东西都是指的一开始给的人物关系图。

但是目前我们只做了一半，还要求所有的可行解。

---

考虑求所有的可行解。

可以发现，每一个可行解都可以通过原来的可行解进行一些操作得到。而这个操作就是把原来的一部分间谍扔到后勤部，再把一部分后勤扔到间谍，改变人数可以为 \(0\)。这是显然的。

直接统计交换数量似乎是不可做的，于是考虑挖掘性质。

因为所有的后勤部的所有人都互相认识，所！以！一！定！不！可！以！连续扔两个人过去！（因为这两个人显然会互相认识，而间谍那里是不允许一条边出现的）。

也就是说，所有其他可行解的间谍部分，一定只包含第一组解的后勤部的某一个点。

同理，所有其他可行解的后勤部分，一定只包含第一组解的间谍部的某一个点。因为间谍部的人两两不认识。

所以最多只能调整一个间谍，一个后勤。

于是，可以得出最多只有四种情况做出调整：

• 一个人都不调整

就是原来的可行解。

• 只从间谍选一个人去当后勤

显然这个间谍需要要求和后勤都认识。

因为 \(n \le 5000\)，我们可以循环它认识的人，看一下是不是所有后勤人员都覆盖了。可以接受，复杂度为 \(O(n^2)\)。

• 只从后勤选一个人去当间谍

同理，可以枚举它所认识的人，看一下是不是所有间谍都不认识。复杂度为 \(O(n^2)\)。

• 从间谍选一个人去当后勤，再从后勤选一个人去当间谍（同时进行）

设这个间谍去后勤的人是 \(a\)，这个后勤去间谍的人是 \(b\)。可以进行 \(O(n^2)\)。

显然 \(a\) 必须要认识除 \(b\) 以外的其他后勤，\(b\) 必须不认识除 \(a\) 以外的其他后勤。

这个可以预处理（因为可以在前两个选择进行处理）已进行 \(O(1)\) 处理。于是还是可以 \(O(n^2)\) 解决。

---

注意一定要判断两组的人数是否都是 \(\ge 1\)，而且初始解可能就不合法（一开始就可能有一边没人）。

#include <bits/stdc++.h>
using namespace std;
const int N = 5010;
bool f[N][N];
vector<int> v[N * 2];
int low[N * 2], dfn[N * 2], ind;
stack<int> stk;
int color[N * 2], s_cnt;
int val[N];//一开始跑出来的解

void tarjan(int u) {
	low[u] = dfn[u] = ++ind;
	stk.push(u);
	for (auto i : v[u]) {
		if (!dfn[i])
			tarjan(i), low[u] = min(low[u], low[i]);
		else if (!color[i])
			low[u] = min(low[u], dfn[i]);
	}
	if (low[u] == dfn[u]) {
		int x;
		s_cnt++;
		do {
			x = stk.top();
			stk.pop();
			color[x] = s_cnt;
		} while (x != u);
	}
}//tarjan
int n;
int cnt[N];
int sum = 0;

int main() {
	cin >> n;
	for (int i = 1; i <= n; i++) {
		int x;
		cin >> x;
		while (x--) {
			int a;
			cin >> a;
			f[i][a] = 1;//使用邻接矩阵记录
		}
	}
	for (int i = 1; i <= n; i++)
		for (int j = i + 1; j <= n; j++) {
			if (f[i][j])
				v[i].push_back(j + n), v[j].push_back(i + n);
			else
				v[i + n].push_back(j), v[j + n].push_back(i);//按照上述方法建图
		}
	for (int i = 1; i <= 2 * n; i++)
		if (!dfn[i])
			tarjan(i);
	for (int i = 1; i <= n; i++) {
		if (color[i] == color[i + n]) {
			cout << "0";
			return 0;
		}//可能会无解！
		val[i] = (color[i] < color[i + n]);//得解
		sum += val[i];//记录一下各有多少个点
	}
	int ans = 1;
	if (sum == 0 || sum == n)
		ans--;//特判，可能有一边没有点
	for (int i = 1; i <= n; i++) {
		if (!val[i])
			continue;
		for (int j = 1; j <= n; j++)
			if (!val[j] && f[i][j])
				cnt[i]++;
		if (cnt[i] >= n - sum && sum >= 2)
			ans++;
	}//把一个间谍加入后勤
	for (int i = 1; i <= n; i++) {
		if (val[i])
			continue;
		for (int j = 1; j <= n; j++)
			if (val[j] && !f[i][j])
				cnt[i]++;
		if (cnt[i] >= sum && (n - sum) >= 2)
			ans++;
	}//把一个后勤加入间谍
	for (int i = 1; i <= n; i++) {
		if (val[i])
			continue;
		for (int j = 1; j <= n; j++) {//i 是后勤，j 是间谍
			if (!val[j])
				continue;
			if (f[i][j])
				cnt[j]--;
			else
				cnt[i]--;//先减去
			if (cnt[i] >= sum - 1 && cnt[j] >= n - sum - 1 && sum >= 1 && (n - sum) >= 1)//先判断能不能成立，再判断一下是否合法
				ans++;
			if (f[i][j])
				cnt[j]++;
			else
				cnt[i]++;//然后还原
		}
	}
	cout << ans << endl;
	return 0;
}

写了这么多，感觉还是有一些紫题的含量的。

P6378 [PA 2010] Riddle

\(n\) 个点 \(m\) 条边的无向图被分成 \(k\) 个部分。每个部分包含一些点。

请选择一些关键点，使得每个部分恰有一个关键点，且每条边至少有一个端点是关键点。判断是否有解。

---

连边是容易的。

因为每个部分都正好有 \(1\) 个点，所以设点集为 \({a_1,a_2,...,a_n}\)，则连 \(\forall 1 \le i,j(i \not = j) \le n,a_i \to -a_j\) 的边。

对于每一条边 \((x,y)\)，有 \(-x \to y\)、\(-y \to x\)。

然后就可以幸福愉快地跑 2-SAT。复杂度达到了残酷的 \(O(n^2)\)，无法通过。

---

因为只有一个部分中的点连边花销较大，边的数量实际上还是 \(n\) 的量级。所以考虑优化一下同一个部分中的点的连边。

这样是我们最开始的连边方式。

但是这样还是太慢了。

这个时候不能删边也不能删点，考虑类似一开始 2-SAT 的方式加点。

我们考虑再建 \(2 \times n\) 个虚点。

对于上面的点，每一个点连向自己的虚点。

对于下面的点，每一个自己的虚点连向自己。

感觉还更乱了。

然后再对于上面的点，每一条出边的起点再设为它的虚点。

然后再对于下面的点，每一条入边的终点再设为它的虚点。

这样就可以开始幸福愉快地删边了！

经过尝试发现这样是合法的，也是可以的。

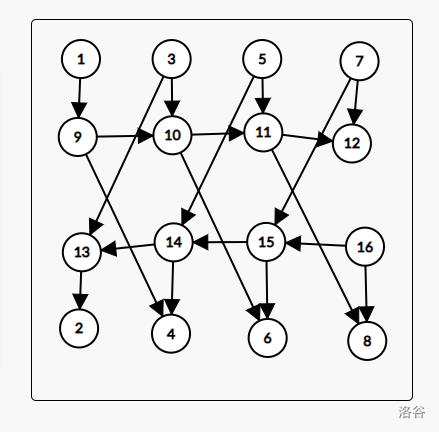
这样，边数又变成了 \(O(n)\)。

注意开 4 倍空间！如果你采用的是链式前向星，也要注意空间（还要开 6 倍）。

#include <bits/stdc++.h>
using namespace std;
const int N = 4000010;
int n, m, k;
vector<int> v[N], p;
int dfn[N], low[N], ind;
stack<int> stk;
int color[N], s_cnt;

void tarjan(int u) {
	dfn[u] = low[u] = ++ind;
	stk.push(u);
	for (auto i : v[u]) {
		if (!dfn[i])
			tarjan(i), low[u] = min(low[u], low[i]);
		else if (!color[i])
			low[u] = min(low[u], dfn[i]);
	}
	if (low[u] == dfn[u]) {
		int x;
		s_cnt++;
		do {
			x = stk.top();
			stk.pop();
			color[x] = s_cnt;
		} while (x != u);
	}
}//tarjan

int main() {
	cin >> n >> m >> k;
	for (int i = 1; i <= m; i++) {
		int x, y;
		cin >> x >> y;
		v[x + n].push_back(y);
		v[y + n].push_back(x);
	}
	for (int i = 1; i <= k; i++) {
		int x;
		cin >> x;
		p.clear();
		while (x--) {
			int a;
			cin >> a;
			p.push_back(a);
		}
		for (auto a : p)
			v[a].push_back(a + 2 * n), v[a + 3 * n].push_back(a + n);
		for (int i = 0; i < (int)p.size(); i++) {
			if (i != 0)
				v[p[i]].push_back(p[i - 1] + 3 * n), v[p[i] + 3 * n].push_back(p[i - 1] + 3 * n);
			if (i != p.size() - 1)
				v[p[i] + 2 * n].push_back(p[i + 1] + n), v[p[i] + 2 * n].push_back(p[i + 1] + 2 * n);
		}//连边，上面讲过。一共有 6 种边，一种都不要忘记
	}
	for (int i = 1; i <= 4 * n; i++)
		if (!dfn[i])
			tarjan(i);
	for (int i = 1; i <= n; i++)
		if (color[i] == color[i + n]) {//直接判断无解即可
			cout << "NIE\n";
			return 0;
		}
	cout << "TAK\n";
	return 0;
}