圆方树学习笔记

首先，圆方树和 Kruskal 重构树差不多，都是将一个无向图转化为了一个特殊性质的树，然后在上面跑各种乱七八糟的算法：LCA、DP、甚至树链剖分……

但是，圆方树和 Kruskal 重构树所基于的东西不同：Kruskal 重构树是基于的最小生成树，而圆方树是基于的点双连通分量。

都是属于一个图重构的知识点。

不会 Kruskal 重构树？不用担心，你以后会学到，这里也不会讲 Kruskal 重构树。

不会点双连通分量？不用担心，你可以见我的其他文章，但是你确实一定得会。

圆方树，顾名思义~~顾名思义吗？~~，包含两种点，一个是圆点，另一个是方点。

圆点代表原图中的点，方点代表原图中的点双连通分量。

圆方树的构建

首先这个图得是一个无向图（因为点双连通分量是在无向图上面的）。

先来看这么一个图：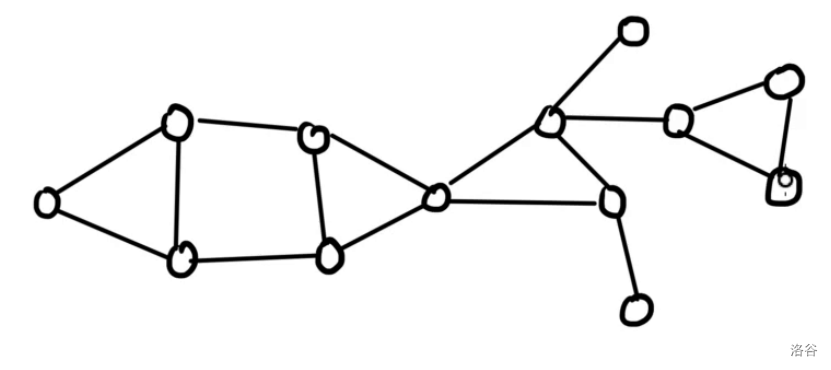

先回忆一下点双连通分量的定义：一个极大连通子图，使得删除任意一个点之后这个子图仍然联通。

先找出所有的点双（使用虚线括出来了），再找出所有的割点（使用蓝色涂色）：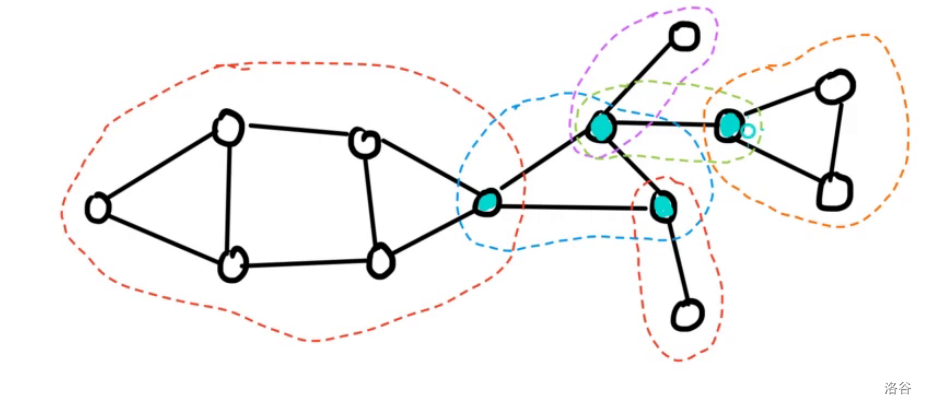

（注：这里有笔误，最下面的一个点属于的点双的颜色重复了，这里从红色改为紫色）

圆方树构建第一步：生成点双的虚拟点（方点）。

我们在点双连通分量中间画出对应颜色的方点：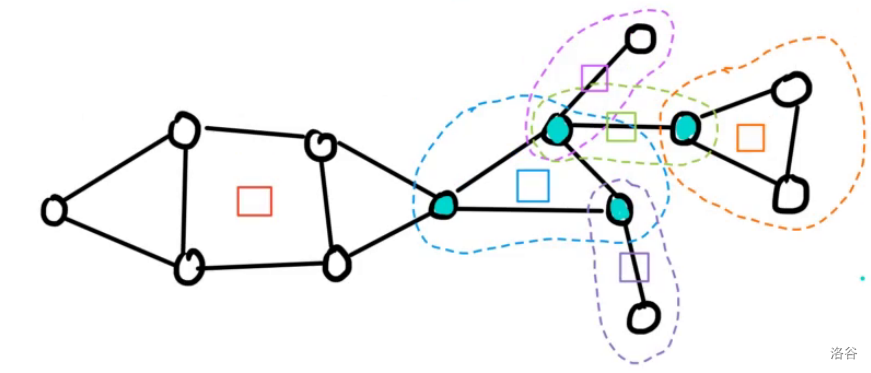

但是这是图重构，所以要把原图中的边全部去掉：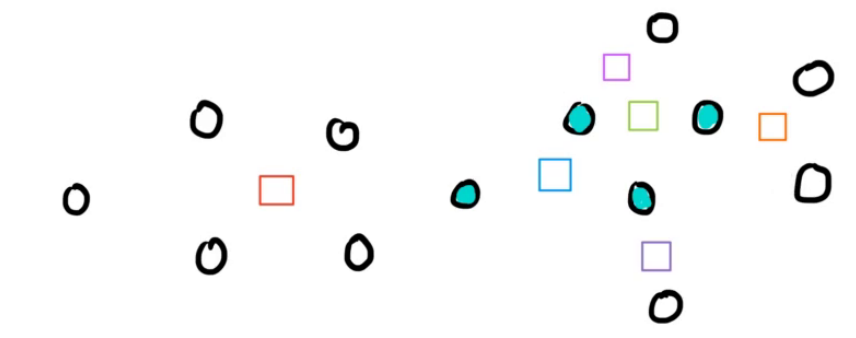

那么怎么将这堆散的点变成一棵树呢？

圆方树构建第二步：点双向内部点连边。

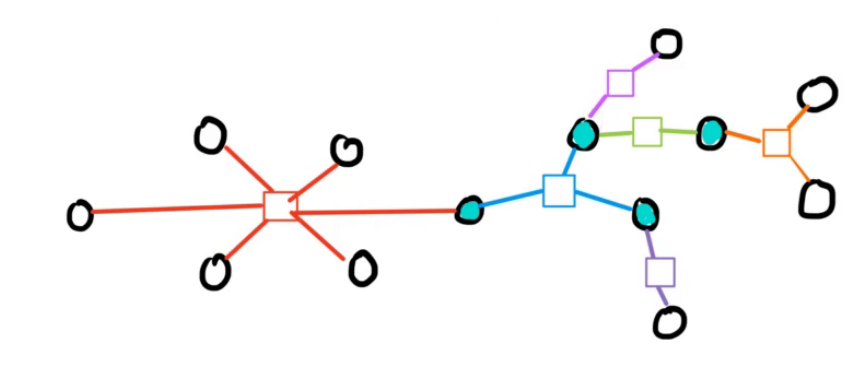
这个东西就是圆方树，无非就是边没有颜色罢了。

圆方树的性质

观察这棵树，你可以发现一些性质吗？

首先，显而易见的性质（~~简称废话~~）：

每一个连通块生成一颗圆方树。（就是圆方树概念的描述）
每一个方点代表一个点双。（同上）
每一个方点连接的圆点就是它点双中的点。（同上）
每一条边必然会连接一个圆点和一个方点（显然的，因为所有的边都是点双（方点）向内部点（圆点）连边）

以上都是显然的结论，不再阐述。

但是经过研究，我们可以发现一些相比较更加好玩的性质：

每一个度大于 \(1\) 的圆点是原图中的割点，每一个度 \(=1\) 的圆点不是割点。

因为我的其他文章里面提到了，相邻点双连通分量所公共的点，一定是割点。

反过来，割点是唯一有可能被相邻点双连通分量共享的点。

被 \(>1\) 个点双连通分量共享，也就是这个点和多个方点相连。

而每一个度 \(=1\) 的圆点，只被自己的唯一一个点双所包含，固然不是割点。

所以就得证了。

圆方树中，两个圆点路径中的圆点，一定是原图中两个点的所有简单路径都必须经过的点。
园方树中，两个圆点的路径中的方点所代表的圆点集合，是原图中两个圆点的所有简单路径可能会经过的点。

这个结论很有用，在之后圆方树大多都是为了使用这个结论。

根据上面几个结论，你能不能猜出圆方树的用法？

圆方树的使用场景：计算两点间必经点与可经点信息或者相关信息，可以考虑圆方树。

圆方树构建模板

#define N 1000100
int n, m, x, y, dfn[N], low[N], tar_index, tar_stack[N], top, cnt;
vector<int> tar_edge[N], rs_edge[N];

void rs_add(int x, int y) {//连边
	rs_edge[x].push_back(y);
	rs_edge[y].push_back(x);
}

void rs_tarjan(int u, int pre) {//点双连通分量，只是做了一些小小的修改
	low[u] = dfn[u] = ++tar_index;
	tar_stack[++top] = u;
	for (auto v : tar_edge[u])
		if (v == pre)
			continue;
		else if (dfn[v] == 0) {
			rs_tarjan(v, u);
			low[u] = min(low[u], low[v]);
			if (low[v] >= dfn[u]) {//找到了点双
				rs_add(u, ++cnt);//当前的割点连入方点
				do {
					rs_add(tar_stack[top], cnt);
				} while (tar_stack[top--] != v);//将其他点双中的点连入方点
			}
		} else
			low[u] = min(low[u], dfn[v]);
}

void get_rs() {
	cnt = n;//cnt为当前点的数量，方便建立新点
	for (int i = 1; i <= n; ++i)
		if (!dfn[i])
			rs_tarjan(i, 0);
}

AT_abc318_g [ABC318G] Typical Path Problem

给你一个无向连通图和三个点 A,B,C，问是否存在一条简单路径，可以从 A 到 B 再到 C。

发现题意可以转化为：问是否存在 A 到 C 的而且经过 B 的一条简单路径。

因为这和“能不能经过”有关，于是考虑圆方树。

建立园方树，dfs A 到 C 的路径，如果在途中发现有 B 的圆点或者是有包含 B 的点双，就是可行的。

否则不可行。

#include <bits/stdc++.h>
using namespace std;
const int N = 400010;//两倍空间，因为圆方树要建虚拟点
int n, m;
int a, b, c;
vector<int> v[N];
int dfn[N], low[N], ind;
int stk[N], top;
int cnt;
vector<int> edge[N];

void add(int x, int y) {
	edge[x].push_back(y);
	edge[y].push_back(x);
}

void tarjan(int u, int pre) {
	low[u] = dfn[u] = ++ind;
	stk[++top] = u;
	for (auto i : v[u]) {
		if (i == pre)
			continue;
		else if (!dfn[i]) {
			tarjan(i, u);
			low[u] = min(low[u], low[i]);
			if (low[i] >= dfn[u]) {
				add(u, ++cnt);
				do {
					add(stk[top], cnt);
				} while (stk[top--] != i);
			}
		} else
			low[u] = min(low[u], dfn[i]);
	}
}

void get() {
	cnt = n;
	for (int i = 1; i <= n; i++)
		if (!dfn[i])
			tarjan(i, 0);
}//前面都是圆方树模板
int r[N], tp;//r是一个栈，为了记录路径

void dfs(int u, int pre) {
	r[++tp] = u;//增加
	if (u == c) {
		for (int i = 1; i <= tp; i++) {
			if (r[i] <= n) {
				if (r[i] == b) {//圆点
					cout << "Yes";
					exit(0);
				}
				continue;
			}
			for (auto j : edge[r[i]])
				if (j == b) {//方点
					cout << "Yes";
					exit(0); 
				}
		}
		cout << "No";
		exit(0);//直接就 exit(0) 了，不用考虑其他的，因为这个时候已经找到了 A 到 C 的唯一路径
	}
	for (auto i : edge[u])
		if (i != pre)
			dfs(i, u);
	tp--;//回溯
}

int main() {
	cin >> n >> m >> a >> b >> c;
	for (int i = 1; i <= m; i++) {
		int x, y;
		cin >> x >> y;
		v[x].push_back(y);
		v[y].push_back(x);
	}
	get();
	dfs(a, 0);
	return 0;
}

P4320 道路相遇

给定一张无向连通图，你需要回答若干次询问：

\(x\) 到 \(y\) 的路径中必经点的数量。

这里就和以前我们讲过的结论对上了，只需要求 \(x \to y\) 的路径中的圆点数量即可。

可以跑 LCA，预处理根结点到这个结点路径上有多少个圆点。

但是这个时候我们需要分类讨论当 lca 是圆点还是方点的答案。

于是这个题就做完了。

另外这个题轻微卡常。

#include <bits/stdc++.h>
using namespace std;
int n, m;
const int N = 2e6+10;
vector<int> v[N];
int dfn[N], low[N], ind;
int stk[N], top;
int cnt;
vector<int> edge[N];

inline void add(int x, int y) {
	edge[x].push_back(y);
	edge[y].push_back(x);
}

inline void tarjan(int u, int pre) {
	low[u] = dfn[u] = ++ind;
	stk[++top] = u;
	for (auto i : v[u]) {
		if (i == pre)
			continue;
		else if (!dfn[i]) {
			tarjan(i, u);
			low[u] = min(low[u], low[i]);
			if (low[i] >= dfn[u]) {
				add(u, ++cnt);
				do {
					add(stk[top], cnt);
				} while (stk[top--] != i);
			}
		} else
			low[u] = min(low[u], dfn[i]);
	}
}

inline void get() {
	cnt = n;
	for (int i = 1; i <= n; i++)
		if (!dfn[i])
			tarjan(i, 0);
}//圆方树板子
int sum[N], f[N][25], dep[N];

inline void dfs(int u, int pre) {
	sum[u] = sum[pre] + (u <= n);//记录一下
	dep[u] = dep[pre] + 1;
	f[u][0] = pre;
	for (int i = 1; i <= 23; i++)
		f[u][i] = f[f[u][i - 1]][i - 1];
	for (auto i : edge[u])
		if (i != pre)
			dfs(i, u);
}

inline int lca(int x, int y) {
	if (dep[x] > dep[y])
		swap(x, y);
	for (int i = 23; i >= 0; i--)
		if (dep[f[y][i]] >= dep[x])
			y = f[y][i];
	if (x == y)
		return x;
	for (int i = 23; i >= 0; i--)
		if (f[x][i] != f[y][i])
			x = f[x][i], y = f[y][i];
	return f[x][0];
}//lca板子

int main() {
	scanf("%d%d", &n, &m);
	for (int i = 1; i <= m; i++) {
		int x, y;
		scanf("%d%d", &x, &y);
		v[x].push_back(y);
		v[y].push_back(x);
	}
	get();
	dfs(1, 0);
	int q;
	scanf("%d", &q);
	while (q--) {
		int x, y;
		scanf("%d%d", &x, &y);
		int l = lca(x, y);
		if (l <= n)
			printf("%d\n", sum[x] + sum[y] - 2 * sum[l] + 1);//分类讨论
		else
			printf("%d\n", sum[x] + sum[y] - 2 * sum[l]);
	}
	return 0;
}

posted @ 2025-04-02 10:46 wusixuan 阅读(38) 评论(0) 收藏举报

刷新页面返回顶部

wusixuan