二分图学习笔记

二分图概念

对于一个图，如果能够把它的点集恰好分成两个部分，使得这第一个部分里面的点两两不连边，第二个部分里面的点也两两不连边，则该图是二分图。或者说每一条边都横跨了两个集合。

举个例子：

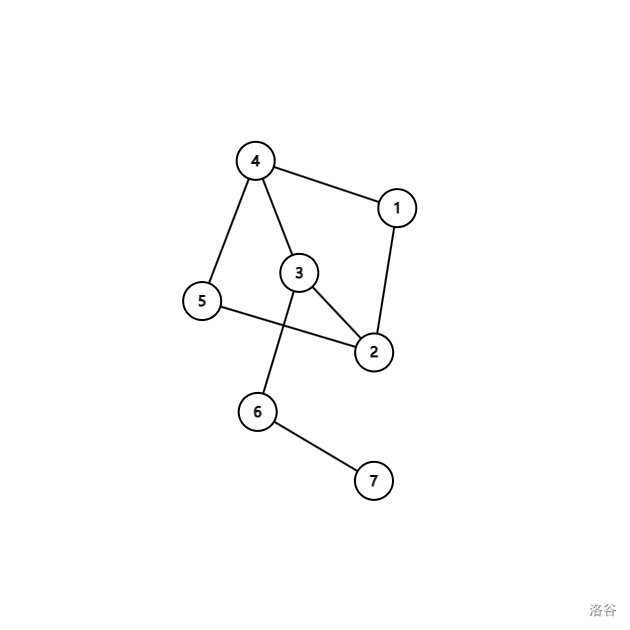
这个图是二分图，因为我们可以将它分成 \(\{1,3,5,7\}\) 和 \(\{2,4,6\}\) 两个点集：

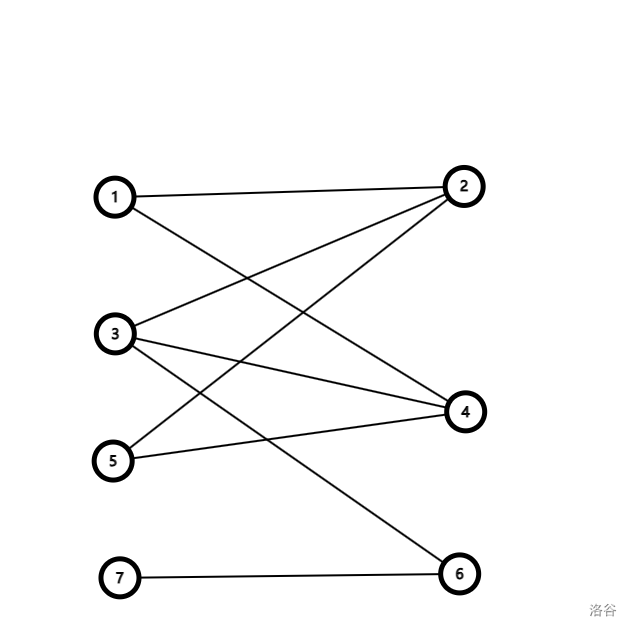
但是这个图：

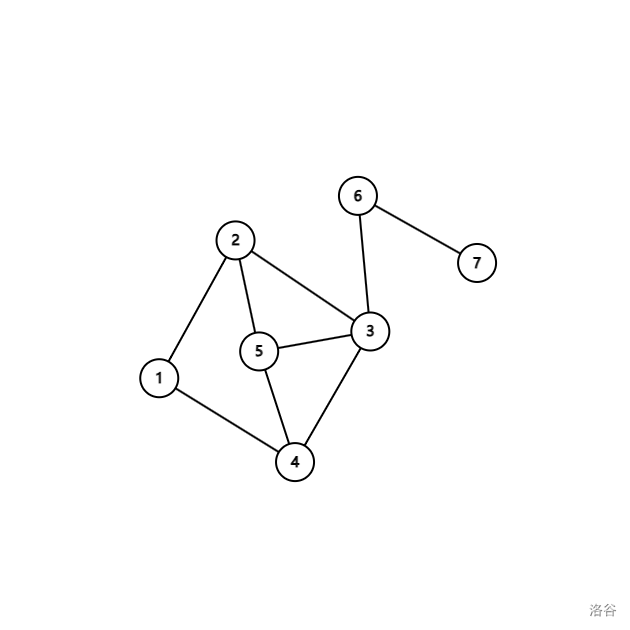
可以发现这个图无论如何也无法划分点集，所以这个图不是二分图。

还是给一下~~不说人话~~的形式化定义：

二分图：如果一张无向图 \((V,E)\) 存在点集 \(A,B\)，满足 \(|A|,|B| \ge 1\)，\(A \cap B = \emptyset\)，\(A \cup B = V\)，且对于任意 \(x,y \in A\) 或 \(x,y \in B\)，\((x,y) \not \in E\)，则称这张无向图为二分图，\(A,B\) 分别称为二分图的左部和右部。

注意，二分图可以不是连通图。

二分图判定

很容易想到一个小学奥数的知识：黑白染色。黑白染色之后若没有冲突的边则就是二分图。

黑白染色就是先任意指定一个点的颜色，然后对于每一条边，都要使两个端点的颜色不同（对应所属于的点集不同），所以每走一条边就变一下颜色。

例如文章自上而下的第一个图黑白染色之后得到：

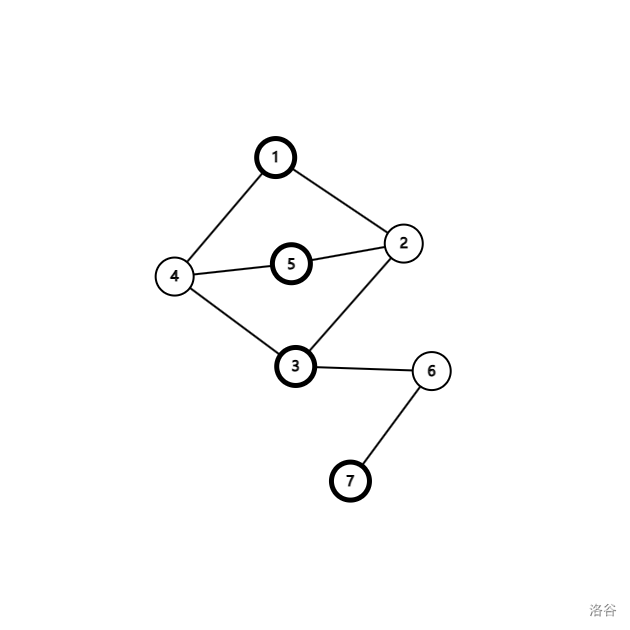
冲突的意思就是一条边的两个端点的颜色相同。因为在同一条边上面，所以这两个点不能在同一个点集。因为这两个点是因为其他边被迫的颜色相同，所以这两个点又不得不在同一个点集里面（如果不在又会发生其他问题）。所以矛盾，所以有冲突的边的图不是二分图。

别急，我们先不立即学二分图匹配，先来看一道题。

CF862B Mahmoud and Ehab and the bipartiteness

题意就是给定一棵树，求至多添加多少条边使得二分图的性质仍然成立。

显然对于这棵树染色，就可以得出无论加多少边二分图的点集一定是什么样子（如果不是这个样子就违背了最基本的树的条件）。

为了最大化边的数量，一定要让左右部尽可能地交叉连边。算出边的数量之后再减去 \(n-1\) 即可。

答案：\(左部点数量 \times 右部点数量 - (n-1)\)。

可以证明，这个值一定不小于 \(0\)。读者可以自己尝试证明一下。

二分图匹配

匹配的定义：在二分图中找到一些边，使得边与边之间没有公共点，那么这组边就是二分图的一种匹配。

最大匹配：边数量最大的匹配。

那么如何求最大匹配呢？这时候就需要请出我们的匈牙利算法（Hungarian Algorithm） 了。

匈牙利算法步骤

假设我们现在已经找出了这样的一组匹配：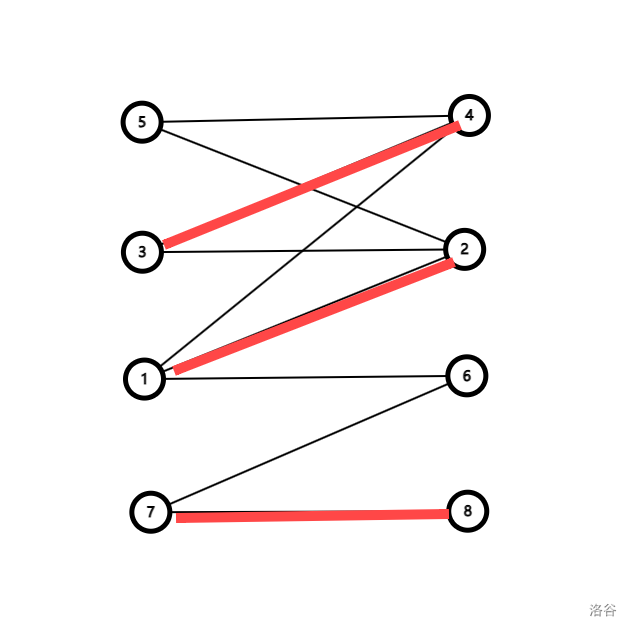

显然，我们还有一个更加优秀的匹配：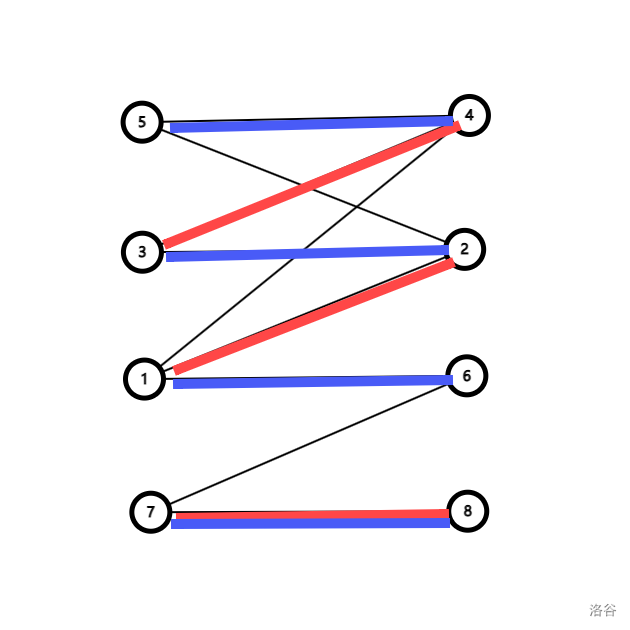

观察上面的三条边，蓝边和红边的关系，我们会发现它们组成了一条路径！

将这个路径弄出来，得到：

黑色边代表还没有被选中的边。而且注意，路径的两头的点一开始都是没有被匹配的，即没有任何一条与其关联的边被选中

是不是可以尝试将选中的边变成没有选中，把没有选中的边变成选中的，从而使答案 \(+1\)。

同时，路径的两头的点也匹配到了。

于是，每找到这样的一条路径，我们的答案就可以增加一个。这个结论在下面会证明。

这条路径的名字名扬四海~~臭名昭著~~，叫做增广路。

所以匈牙利算法本质就是在干找增广路这个过程。

不妨先来看一下它是怎么执行（搜索）的：

还是那张图。

先从 \(5\) 开始，因为 \(5\) 没有对应的点，所以可以选一个。

\(5\) 首先找到了 \(4\)，但是 \(4\) 说它已经有对应点了。

这时候可以放弃，但 \(5\) 就不会有对应点了。
这时候也可以穷追不舍，那得看 \(3\) 的态度：先把 \(3\) 的对应点~~剥夺了~~，然后看 \(3\) 能不能找到其他的对应点。

然后 \(3\) 找到了 \(2\)，还要看 \(1\) 能不能找到对应点。

然后 \(1\) 找到了 \(6\)，这个时候，\(6\) 恰好没有对应点，所以 \(1\) 可以和 \(6\) 对应，找到了一条增广路。

观察以上的步骤，我们可以发现一个规律：每一次搜索都是左部点寻找右部点，然后右部点直接去其对应的左部点。所以在搜索的过程中，还需要同步记录每一个右部点对应的左部点。

匈牙利算法模板

算法的设计是每次都要从一个左部点找增广路，复杂度是 \(O(numA * m + numB)\) 的，其中 \(numA,numB\) 代表左部、右部的点数，\(m\) 表示边数。

因为进行了左部点数量次增广路查找，每次都会搜全图，所以是这个复杂度。

其实我看这个复杂度很不顺眼：这么神秘的一番推导咋推出一个平方级的玩意？

当然你要是得出线性做法，这个算法就不叫匈牙利算法了。

另外有一个结论：答案一定不超过 \(\min(numA,numB)\)。显然。

#include <bits/stdc++.h>
using namespace std;
#define int long long
#define N 1000010

int num, res[N], vis[N];
//res[]:右部点的对应点
vector<int> edge[N];

bool match(int u) {
	if (vis[u] == 1)
		return 0;
	else
		vis[u] = 1;
	for (auto v : edge[u])//注意，为了使点的编号不重复，在主函数采用顺序编号，即将右部点的编号全部加上一个 numA
		if (res[v] == 0 || match(res[v]) == 1) { //对方没有对应点，或者对方的对应点可以去找另外一个右部点
			res[v] = u;//增广路上更新匹配
			return 1;
		}
	return 0;
}//O(n + m)

int hungarian() {
	int cnt = 0;
	for (int i = 1; i <= numA; ++i) {
		memset(vis, 0, sizeof(vis));//清空
		cnt += match(i);//如果找到增广路，答案加一
	}
	return cnt;
}//O(numA * m + numB)

匈牙利算法正确性证明

你别看这个算法模板非常的简单，但是这个算法下面的那个函数怎么说都是不对劲的：为什么每一个左部点找一次增广路，就可以得到答案？

我们分类讨论每一个左部点的情况，有以下三种：

这个点已经被匹配到了，不存在增广路。不需要短期内再跑一次增广路。
这个点还没有被匹配，若找到了增广路变成匹配。也不需要短期内再跑一次增广路。
试过了，没有找到增广路，无法匹配。也不需要再跑一次。

这个时候又会有同学问了：现在匹配不了不代表未来匹配不了。

假设在未来形成的增广路的一头是 \(A\) 点，一头是 \(B\) 点，\(A \to B\) 形成了增广路，且在一开始，\(B\) 没有找到增广路。

这时候就需要分类讨论一下。

1.这条增广路中途的选过的边和没有选过的边在中途没有被改过。

那我为什么不能从一开始就从 \(B \to A\) 走增广路？？？

然后就有一个发现：增广路的两头是等价的啊！我可以从一端搜到另一端找到增广路，我为什么不能从另一端搜到这一端找到增广路？

于是这个子问题就被解决了。

2.这条增广路中途的选过的边和没有选过的边在中途发生了改变。

那么改变这条增广路径的增广路一定也可以和 \(B\) 凑成另一条增广路，也是矛盾的。

可以画图理解一下。

所以每一个点找一次增广路，足矣！

然后因为每一个点都会把增广路找尽，所以在算法执行完毕之后不会存在增广路。

那么得出：

如果一个点找到了增广路，那么一定可以对答案构成 \(1\) 的贡献。
如果一个点没有找到增广路，那么这个点这辈子也不会被答案构成贡献了，不需要在之后考虑。

你说得对，我们解决了一个问题，但是正确性还没有完全解决。

接下来还有一个问题：

question:为什么没有增广路的时候，就一定是最大匹配了？

我们可以证明还有增广路的时候，答案就一定不是最大匹配。

但是我们无法根据这个证明没有增广路的时候，答案就一定是最大匹配。

我们使用反证法来解决这个问题：

反证：如果没有增广路，但还是找到了一个更大的匹配，是什么样子的。

再用一下这张图：

不妨再次分类讨论，蓝色边的情况（这里我们只讨论上面的三个蓝色边和两个红色边）：

1.某一条蓝色边的两边的点都没有被匹配

那这条边本身就是增广路啊！我们可没有规定增广路的长度一定 \(>1\)。

那么就矛盾了。

2.每条边的恰好一个点是匹配点

观察到红边一定比蓝色边少，所以还是相连的形式。

那么又出现了增广路，然后又矛盾了。

3.有些边的两个点是匹配点

这个不需要管。可以意会一下。

于是怎么样都是矛盾的，这个问题也被解答了。

P1129 [ZJOI2007] 矩阵游戏

我们来看一道题。

题面：有一个 \(01\) 的 \(n\times n\) 棋盘，可以随意交换任意行和任意列，问主对角线能否全部变成 \(1\)。

在这种交换来交换去的题目中，我们需要抓住其中的不变量：同行或同列的点无论经过多少次变换仍然同行或同列。

而主对角线上面有 \(n\) 个不同行不同列的点，所以我们只需要在原棋盘中找出 \(n\) 个不同行不同列的 \(1\) 即可。

这时候需要请出经典 trick：把行号作为左半边点，把列号作为右半边点，\(1\) 的位置看成连接行和列的边。

然后可以直接跑最大匹配，看一下是否 \(=n\) 即可（即找出 \(n\) 条连接行列的边也就是 \(1\) 的位置，这些边没有公共点也就是不同行不同列）。

因为 \(numA=numB=n,m=O(n^2)\)，所以匈牙利算法的复杂度就是 \(O(n^3)\)，可以通过。

Koenig（柯尼希）定理

首先，我们需要明确一些定义。

最小点覆盖：在二分图中选最少的点，使得每一条边都至少有一个点选中。

柯尼希定理：二分图的最小点覆盖 = 最大匹配。就这么一句话，没了。

我们来尝试证明一下。

1.最小点覆盖 \(\ge\) 最大匹配

很显然。

因为最大匹配没有公共点，所以必须每一条边至少选一个点。

2.最小点覆盖 \(\le\) 最大匹配

结论：覆盖点的所有边中，至少有一条的另一端不是覆盖点。这个很显然，可以自己画个图。

把每一个覆盖点到非覆盖点的边选一条，那么一定是匹配的。

反例：如果两个覆盖点的边在一个非覆盖点公共邻居，那么去掉它们选邻居结果更优，就矛盾了。

两个东西结合起来，这个就证明完了。

最大独立集

最大独立集：在图中选出最多的点，使得任意两点之间没有边。

最大独立集 = \(n\) - 最小点覆盖。

好像最大独立集和最小点覆盖是一个天然互补的关系？？？好像是真的。

最小路径覆盖

就是对于一个有向图，求最少需要多少条简单路径，使得整个图的结点都被覆盖。

最小路径覆盖 = 整个图的结点数量 - 最大匹配。

拆点 trick

当你面对的不是一个二分图怎么办？？？

如果你这个有向图不是 DAG，老天爷都救不了你。

如果你这个有向图是 DAG，我可以救你！

trick：将每一个点拆成 u,v 两个点，所有连向这个点的边统统改为连向 u，所有从这个点连出来的边统统改为从 v 连出来。

然后这就转化为了一个二分图。

posted @ 2025-03-29 08:57 wusixuan 阅读(5) 评论(0) 收藏举报

刷新页面返回顶部

wusixuan