图论学习笔记2

请先阅读图论学习笔记 1。

在这篇文章里，我们将继续以前 tarjan 求解的强连通分量和双连通分量，讲解其缩点相关内容。

也会讲解一些特殊的图：基环树与仙人掌图、最小树形图。

缩点

我们知道，将强连通分量、双连通分量缩点之后会形成一棵树。

在学术上，我们将边双连通分量缩点之后的树称为 Bridge Tree，点双连通分量缩点之后的树称为 Block-Cut Tree，强连通分量缩点之后的树称为 SCC DAG。

缩点除了写法没什么好讲的，而且有一些已经在 图论学习笔记 1 中涉及到。就是将连通分量变成一个点，在相同连通分量中点之间的边隐藏，只保留连通分量之间的边。

先看题。

CF1000E We Need More Bosses

*2100，好像没多难。

题目大意：给定一个 \(n\) 点 \(m\) 边的连通无向图，需要找到两个点 \(s,t\)，使得 \(s\) 到 \(t\) 必须要经过的边最多，即使 无论怎么走都会经过 的边最多。

我们很容易发现这东西和边双连通分量扯上了关系，因为边双连通分量的定义是：极大的，其中任意两个点之间至少有两条不重合的路径的连通子图。

显然，如果 \(s\) 到 \(t\) 在同一个边双连通分量内，它们必须要经过的边一定为 \(0\) 条。

从而我们可以得出，\(s\) 到 \(t\) 之间必须要经过的边，全部都是桥。

于是不妨想到对边双连通分量缩点。画图可以得到，必须要经过的边一定是 Bridge Tree 上面 \(s\) 和 \(t\) 处于的边双连通分量（假定为 \(x\) 和 \(y\)）之间的路径。

于是问题变成了这样：给定一棵树，需要你求上面的最长路。

这不就是树的直径吗！当然这里可能有一些难写。

也有另一种做法：枚举 \(lca\) 的位置，显然 \(x\) 和 \(y\) 一定是在 \(lca\) 的子结点的不同的子树里面（要不然它们的 lca 就不是 \(lca\) 这个值了），设为 \(T_1\) 和 \(T_2\)。

要使路径长度最长，需要使 \(x\) 在 \(T_1\) 中深度最大的位置，\(y\) 也在 \(T_2\) 中深度最大的位置。

显然一个子树中的深度最大位置可以使用树形 dp来求，是基础中的基础了。

然后要算答案的时候，直接取子结点的子树最大深度 的 最大值和次大值 相加即可。

补充：另外，还有可能是 \(lca\) 和子树中的一个点，直接使用整个子树深度最大更新即可。

这道题就这么做完了，思维含量真的不高，*2100 可能是边双连通分量的加成。

#include <bits/stdc++.h>
using namespace std;
int n, m;
const int N = 300010;
vector<int> v[N];//原图
set<int> edge[N];//缩点之后的图
int p[N], dfn[N];//下面开始跑边双连通分量
int num[N], cnt;

int find(int x) {
	if (p[x] == x)
		return x;
	return p[x] = find(p[x]);
}

void tarjan(int u, int pre) {
	dfn[u] = ++cnt, num[cnt] = u;
	p[dfn[u]] = dfn[u];
	for (auto i : v[u]) {
		if (!dfn[i])
			tarjan(i, u), p[dfn[u]] = min(p[dfn[u]], p[dfn[i]]);
		else if (i != pre)
			p[dfn[u]] = min(p[dfn[u]], dfn[i]);
		else
			pre = 0;
	}
}
//---到上面全是板子
int dp[N], dep[N];//准备树形dp
//dp[u]表示u的子树内的最大深度
int ans = 0;//答案

void dfs(int u, int pre) {
	dep[u] = dep[pre] + 1;//先更新自己的深度
	dp[u] = dep[u];//自己的子树显然包含自己
	int mx = 0, sc = 0;//记录最大值和次大值
	for (auto i : edge[u]) {
		if (i == pre)
			continue;//这里的树是无根树，所以需要判断
		dfs(i, u);//递归
		dp[u] = max(dp[u], dp[i]);//先更新自己的dp值
		if (dp[i] >= mx)//更新最大值和最小值
			sc = mx, mx = dp[i];
		else if (dp[i] >= sc)
			sc = dp[i];
	}
//顺便更新答案
	ans = max(ans, sc + mx - 2 * dep[u]);//情况1：s 和 t 在两个不同的子结点的子树内
//注意还要减去自己深度的两倍
	ans = max(ans, dp[u] - dep[u]);//情况2：s 和 t 有一个是自己，另一个是自己的后代
}

int main() {
	cin >> n >> m;
	for (int i = 1; i <= m; i++) {
		int x, y;
		cin >> x >> y;
		v[x].push_back(y);
		v[y].push_back(x);
	}
	tarjan(1, 0);
	int rt = 0;//随便选一个根
	for (int i = 1; i <= n; i++)
		for (auto j : v[i])
			if (find(dfn[i]) != find(dfn[j])) {//只保留边双连通分量之间的边
				edge[find(dfn[i])].insert(find(dfn[j]));
				edge[find(dfn[j])].insert(find(dfn[i]));
//注意这里的 i 和 j 都要套上一层 dfn[]，因为 find 是使用的深搜树上编号
//find 返回的也是树上编号，但这里无关紧要，所以不需要使用 num 转换。我们关心的是树的结构
				rt = find(dfn[i]);//记录根
			}
	if (rt == 0) {//注意，如果整个图是一个边双连通分量，则这里的 rt 为 0，如果搜索可能会出现问题
		cout << "0";//显然当整个图是边双连通分量的时候没有必须经过的边
		return 0;
	}
	dfs(rt, 0);//树形dp
	cout << ans << endl;
	return 0;
}

CF652E Pursuit For Artifacts

结论题。

不难注意到一件事情：一个环上面如果有一条边权为 \(1\) 的边，则环上面所有的点一定都可以存在有一条 \(1\) 的路径。

环你想到了什么？没错，边双连通分量。

考虑证明更加高级的结论：如果一个边双连通分量里面有至少一条边权为 \(1\) 的边，则边双连通分量里面所有的点一定都可以存在一条 \(1\) 的路径。

取边双内任意一条边权为 \(1\) 的边，设其两端为 \(x,y\)。

我们可以将边双连通分量看成环套环的形式。

先找到同时包含 \(x,y\) 的环。根据边双连通分量任意两个点都有两条无重复的路径，一定存在这个环。

将这个环设为1 级环。

将 1 级环缩点，然后再找到一个更大的环，完全包含这个环：

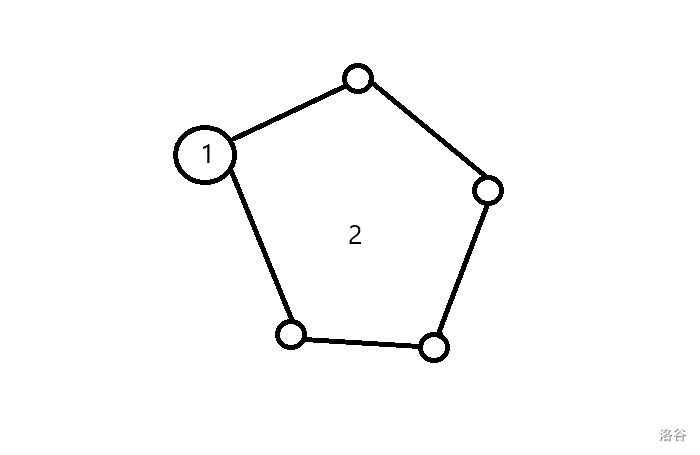
称为二级环。

以此类推。

这样子，任意边双连通分量的点，都可以通过环上穿梭的形式经过这条边权为 \(1\) 的边。结论得证。

---

但是如果两个点不在同一个边双连通分量中呢？

不妨先缩点。

这设两个点所在的边双编号为 \(u,v\)。

则显然可以直接判断 \(u \to v\) 的路径中的所有边双连通分量和桥里面的边有没有边权为 \(1\) 的边即可。

因为只有一次询问，复杂度为 \(O(n)\)。

---

下面开始讲强连通分量缩点。

强连通分量缩点之后会形成 \(SCC DAG\)，也就是一个有向无环图。

有向无环图之后问题就可以变得简单了：可以变成 DAG 上 DP，也可以考其他内容。

提供一个自己总结的，一般性的解题方式：缩点之后，思考此时scc的意义。再思考此时答案有什么意义，怎么求出来。

还是以前讲过了，直接看题吧。

P3627 [APIO2009] 抢掠计划

题面已经讲得足够清楚。

首先这是一个有向图，而且需要注意，他可以经过同一路口或道路任意多次。

所以可以得出：同一个强连通分量的点可以随便走。

于是这个劫匪可以先把自己的强连通分量里面的点全都给抢了，然后再考虑抢其他强连通分量里面的点。

---

可以枚举终点 \(T\)，然后考虑从起点 \(S\) 到终点 \(T\) 最多可以抢多少。

我们发现一个事实：当这个劫匪到达了一个强连通分量的时候，可以把里面所有的东西都给抢了。即使这个强连通分量不是 \(S\) 一开始的强连通分量。

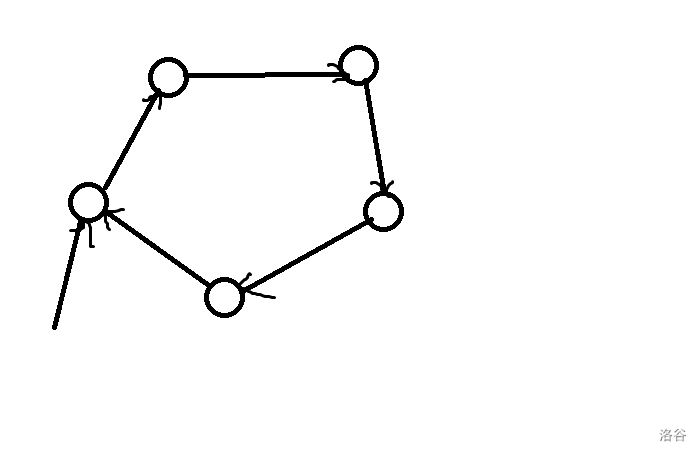
具体地，可以这么走：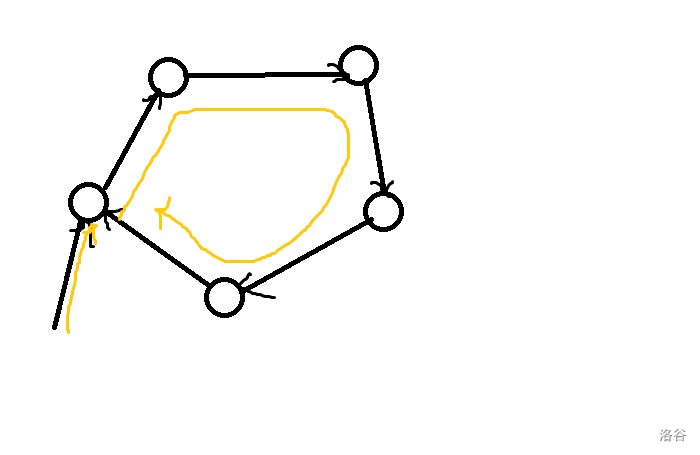

于是得到一个很好玩的事情：这时候就可以使用点权，SCC DAG 上面的点权就是强连通分量里面所有点的点权和。

于是就转变成了喜闻乐见的 DAG DP 经典问题，这样枚举 \(T\) 的时候可以直接查表。

---

P3119 [USACO15JAN] Grass Cownoisseur G

显然如果不走反边，从 \(1\) 开始，最多也只能走完自己强连通分量的点。

于是得到结论：当到达了一个新的强连通分量，这个强连通分量里面所有的点都可以被走到。

所以可以采用赋值点权的做法：每一个强连通分量缩点之后的点权都是其内部的点的数量。

但是如果要走反边的话，这就有一点难办啊……

尝试使用常规套路：直接枚举反边到底是哪一条。

因为这个时候答案只和强连通分量有关，所以设 这条反边的两端 属于的强连通分量 分别是 \(u,v\)，并设 \(1\) 属于的强连通分量是 \(w\)。

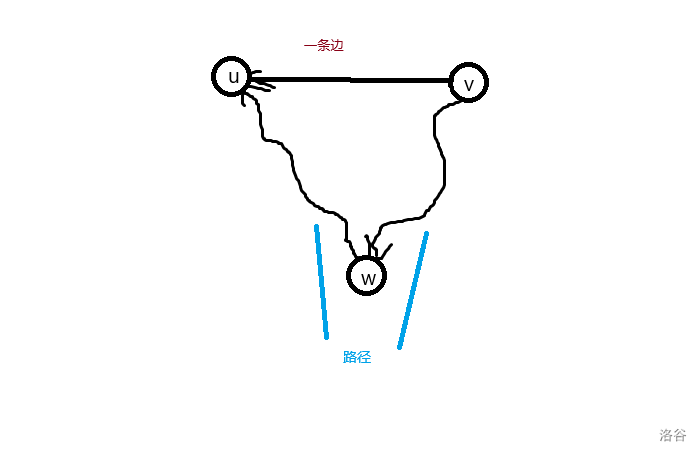
这里就不妨设存在 \(w \to u\) 和 \(v \to w\) 的路径，而 \((u,v)\) 这条边的方向并不重要。

调转过来之后就变成了这样：

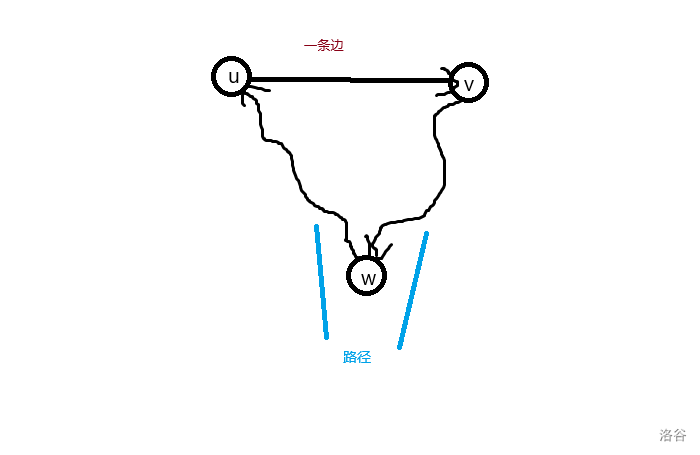
发现，这个时候，可以从 \(w \to u \to v \to w\)！也就是构成了一条合法的路径！

这时候，我们需要计算图中的路径（不包括 \(u \to v\) 的一条边，也就是 \(w \to u\) 和 \(v \to w\) 这两条路径）构成的贡献。

设 \(dp1_i\) 表示从 \(w\) 走到 \(i\) 的一路上途径的最大点权和，不包括 \(w\) 自己。正向跑 dijkstra 或者是拓扑排序都可以。

设 \(dp2_i\) 表示从 \(i\) 走到 \(w\) 的一路上途径的最大点权和，不包括 \(w\) 自己。可以直接建反向图，然后跑 dijkstra 或者是拓扑排序就可以了。

对于 \(u \to v\) 的这一条边，答案就是 \(dp1_u+dp2_v\)。直接预处理出 \(dp1,dp2\) 然后就可以直接获取答案。

---