平衡树学习笔记
平衡树分很多种,有 Treap、FHQ_Treap、Splay、sbt、AVL……在竞赛中,FHQ_Treap 和 Splay 较为常用,其余的了解一下即可,这里不详细讲了。
(当然我还会讲一下 BST 和 Treap)
平衡树是一种数据结构,总体实现相较于线段树比较复杂,而且有一些问题使用平衡树和线段树都可以得到解决。解决这些问题时,推荐使用线段树。
但是平衡树同线段树一样,也有其“专利”,即线段树维护不了但平衡树可以维护的操作。例如区间翻转。
在一些线段树题目中,可以观察题目特有的“区间翻转”操作的性质,从而使用“不正确的解法”解决这个问题。但是平衡树却可以直接适用于这个操作。
另外,平衡树也支持其他的操作。
BST
二叉搜索树(Binary Search Tree,简称 BST)是一个以递归的形式定义的数据结构,其有五个特点:
-
1.是一个二叉树
-
2.每一个结点都带有一个权值
-
3.当前结点的左子树中的任何一个点的权值都严格小于当前结点的权值(如果有),当前结点的右子树中的任何一个点的权值都严格大于当前结点的权值(如果有)。
-
4.不同结点的权值不同,如果操作中出现了相同的结点则可以在每一个结点上面记录一下结点的权值出现次数。
-
5.很重要的性质:在树上面中序遍历得到的数组,从左到右单调递增。
维护操作:
增加一个值
从根结点开始二分即可,如果发现遍历到了叶结点就在叶结点下面加上这个值。
删除一个值
仍然是从根结点开始二分,如果发现这个值存在了就有两种情况:
-
这个值出现次数大于二次:将次数减去 \(1\) 即可。
-
这个值出现次数只剩一次了:
-
如果这个值在叶结点的位置:直接删除叶结点。
-
如果这个值只有一个儿子:直接把自己的儿子挂上去,然后自己删掉。
-
如果其有两个儿子:可以取左子树的最大值或者是右子树的最小值来代替它,然后删除它即可。
-
找前驱/后继
假设我们需要找前驱,找后继的过程和找前驱的原理差不多。
-
存在左子树,显然前驱就是在左子树的位置,然后就是找左子树的最大值,下面会讲。
-
不存在:
- 则一直往父结点遍历,直到发现有一祖先(包括这个点自己)是其父亲的右儿子,这个父亲就是前驱。
找最大值/最小值
最大值就是从根一直往右走。
最小值就是从根一直往左走。
容易发现,上述的 4 种操作,set 里面都是有的。
不过二叉搜索树还有一些 set 不支持的操作。
求某个值的排名
显然,set 里面没有任何支持排名的函数,除了第 \(1\) 名和最后一名。
但是这个 BST 可以轻松维护。
这时候,我们还需要在 BST 的结点上维护一个新值:以这个点为根的子树大小。
这样我们就可以使用二分的方法来求了。
求某个排名对应的某个值也可以这么做。
容易发现,BST 的每次操作复杂度平均是 \(O(\log n)\) 的。但也只是平均,仍然存在各种极端情况。
这里不贴 BST 模板代码,因为 BST 在实际场景中没有很大用处,也是因为其太好卡了。
假设我们一开始加入一个值 \(a_1\),然后加入小于 \(a_1\) 的值 \(a_2\),再然后加入小于 \(a_2\) 的值 \(a_3\)……最后,在加入 \(n\) 个元素之后,BST 的形状就是一条链。
当我们执行上面的操作时,大部分操作都是 \(O(n)\) 的,这会让其的性能大大下降。
我们不妨思考这样一个问题:如果将 BST 的根换一下,换成链的中间位置,就可以使复杂度除以 \(2\);如果再将这两个子树的根换一下,复杂度又可以除以 \(2\)……
没错,这就是 Treap 的想法。为了让时间复杂度尽量的平均,需要使 BST 的形状尽量均衡随机,这样就可以达到一个期望复杂度的效果。
Treap
Treap 是两个单词通过拼接而得到的组合词,这两个单词分别是 Tree 和 Heap。即 树 和 堆。
顾名思义,Treap 的原理和一种树和一种堆有关,这种堆就是大根堆,这种树就是二叉搜索树。
可以理解为 Treap 就是一种特殊的二叉搜索树。
考虑在每个结点上再设立一个随机值。(随机值不是权值)然后我们需要维护这个 Treap,让其永远是一个在随机值基础上的大根堆。这也是 Heap。
因为每一个随机值都是随机得来的,因此以其为基础的大根堆肯定形状比较均摊,几乎不可能是一条链。
但是我们在插入和删除的时候很有可能会使这个大根堆的性质被破坏。(这里解释一下。你插入一个点,随机了一个权值之后,这个大根堆很有可能会不满足要求)所以我们需要采取一些方式来维护这个堆的性质,这个方式就是旋转。
将某一个儿子和其父亲交换位置,即将这个父亲变成其左儿子 / 右儿子的右儿子 / 左儿子,并将左儿子、右儿子设为新的根。旋转的方向还得看赋予的随机值的大小关系。
与左儿子交换的操作称为右旋(zig),与右儿子交换的操作称为左旋(zag)。
以右旋为例子。
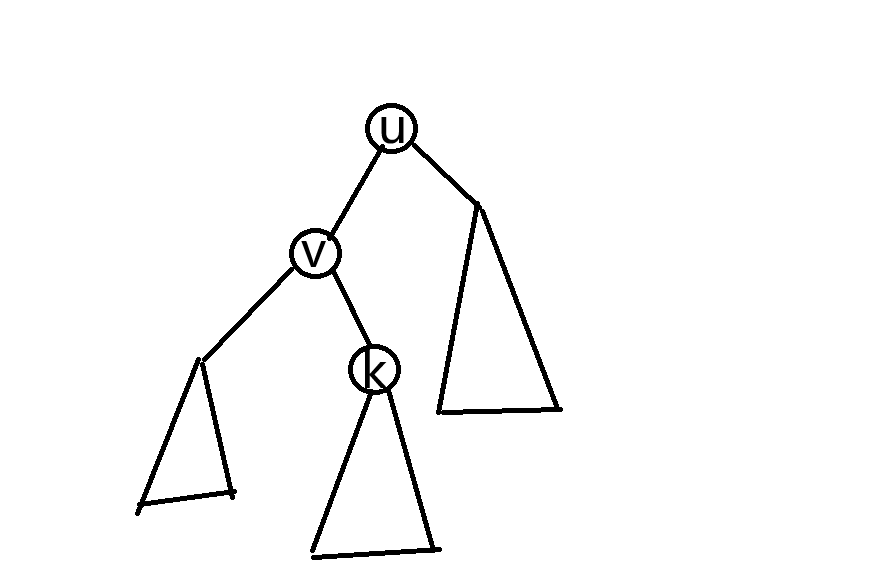
我们现在需要将 \(u\) 的左端点 \(v\) 提到 \(u\) 的父亲的位置。但是会发现如果这时候 \(u\) 直接作为了 \(v\) 的子结点,那么 \(v\) 会可能会有 \(3\) 个子结点,而且 \(u\) 还少了一个左儿子,这样就甚至不是一个二叉搜索树了。
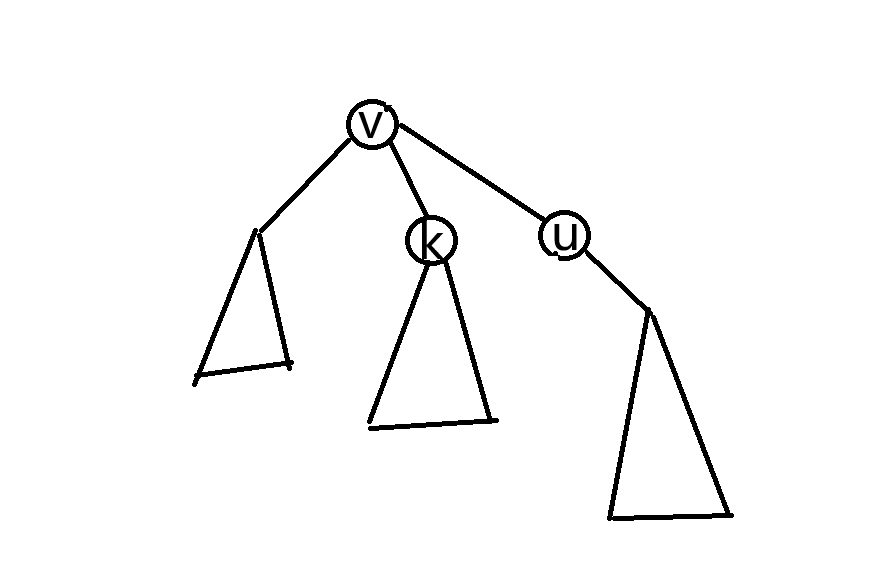
所以我们要在旋转的时候,让 \(u\) 将一个 \(v\) 的子结点据为己有以弥补这个状况。
因为 \(v\) 子树里面的所有东西的权值都小于 \(u\),所以 \(u\) 要将原本 \(v\) 的右子树作为其左儿子。
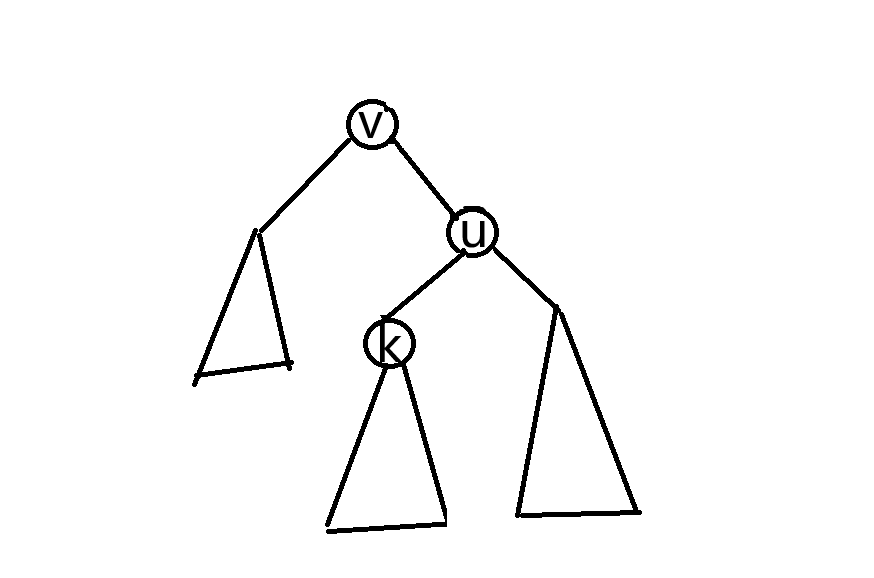
左旋和右旋就差不多的,反过来即可。
观察得知,不管怎么左旋和右旋,Treap 的中序遍历总是不变。
可以证明,在一般情况下,Treap 的时间复杂度是 \(O(\log n)\) 的。因为其用于维护堆的值完全是随机的。
而这里也普及一个小知识点:在一般情况下,随机的树的高度期望为 \(\log n\)。
Treap 模板
模板题目:P3369 【模板】普通平衡树。
struct Node {
int l, r; // 左右子结点索引
int key; // 结点的键值(用于二叉搜索树排序)
int val; // 结点的随机值(用于维护堆性质)
int cnt; // 当前键值的重复次数
int size; // 子树总大小(包括所有重复值)
} tr[N]; // 静态结点池
int root, idx; // 根结点索引和结点计数器
// 更新子树大小
void pushup(int p) {
tr[p].size = tr[tr[p].l].size + tr[tr[p].r].size + tr[p].cnt;
}
// 创建新结点
int new_node(int key) {
tr[++idx].key = key;
tr[idx].val = rand(); // 随机优先级
tr[idx].cnt = 1;
tr[idx].size = 1;
tr[idx].l = tr[idx].r = 0; // 初始无子结点
return idx;
}
// 右旋(提升左子结点为根)
void zig(int &p) {
int q = tr[p].l;
tr[p].l = tr[q].r; // 原左子结点的右子树挂到当前结点左侧
tr[q].r = p; // 当前结点成为新根的右子结点
p = q; // 更新根为原左子结点
pushup(tr[p].r); // 更新原根的子树大小
pushup(p); // 更新新根的子树大小
}
// 左旋(提升右子结点为根)
void zag(int &p) {
int q = tr[p].r;
tr[p].r = tr[q].l; // 原右子结点的左子树挂到当前结点右侧
tr[q].l = p; // 当前结点成为新根的左子结点
p = q; // 更新根为原右子结点
pushup(tr[p].l); // 更新原根的子树大小
pushup(p); // 更新新根的子树大小
}
// 插入操作
void insert(int &p, int key) {
if (!p) {
p = new_node(key); // 空位置直接插入
return;
}
if (tr[p].key == key) {
tr[p].cnt++; // 重复键值,计数增加
} else if (tr[p].key > key) {
insert(tr[p].l, key); // 插入左子树
if (tr[tr[p].l].val > tr[p].val) {
zig(p); // 左子结点优先级更高,右旋调整
}
} else {
insert(tr[p].r, key); // 插入右子树
if (tr[tr[p].r].val > tr[p].val) {
zag(p); // 右子结点优先级更高,左旋调整
}
}
pushup(p); // 更新当前结点子树大小
}
// 删除操作
void remove(int &p, int key) {
if (!p) return; // 结点不存在
if (tr[p].key == key) {
if (tr[p].cnt > 1) {
tr[p].cnt--; // 减少计数即可
} else {
// 若结点有子结点,需旋转至叶子再删除
if (tr[p].l || tr[p].r) {
if (!tr[p].r || (tr[p].l && tr[tr[p].l].val > tr[tr[p].r].val)) {
zig(p); // 右旋
remove(tr[p].r, key); // 递归删除原结点
} else {
zag(p); // 左旋
remove(tr[p].l, key);
}
} else {
p = 0; // 叶子结点直接删除
}
}
} else if (tr[p].key > key) {
remove(tr[p].l, key); // 在左子树中删除
} else {
remove(tr[p].r, key); // 在右子树中删除
}
if (p) pushup(p); // 非空结点需更新大小
}
// 查询 key 的排名(小于 key 的数的数量 + 1)
int get_rank(int p, int key) {
if (!p) return 0;
if (tr[p].key == key) {
return tr[tr[p].l].size + 1;
} else if (tr[p].key > key) {
return get_rank(tr[p].l, key);
} else {
return tr[tr[p].l].size + tr[p].cnt + get_rank(tr[p].r, key);
}
}
// 查询排名为 rank 的数值
int get_key(int p, int rank) {
if (!p) return INF;
if (tr[tr[p].l].size >= rank) {
return get_key(tr[p].l, rank);
} else if (tr[tr[p].l].size + tr[p].cnt >= rank) {
return tr[p].key;
} else {
return get_key(tr[p].r, rank - tr[tr[p].l].size - tr[p].cnt);
}
}
// 查询 key 的前驱(最大的小于 key 的数)
int get_prev(int p, int key) {
if (!p) return -INF;
if (tr[p].key >= key) {
return get_prev(tr[p].l, key);
} else {
return max(tr[p].key, get_prev(tr[p].r, key));
}
}
// 查询 key 的后继(最小的大于 key 的数)
int get_next(int p, int key) {
if (!p) return INF;
if (tr[p].key <= key) {
return get_next(tr[p].r, key);
} else {
return min(tr[p].key, get_next(tr[p].l, key));
}
}
FHQ - Treap
https://www.cnblogs.com/sea-and-sky/p/18414461
mt19937 xxx;//这里的xxx可以自由随意替换
srand(time(NULL));//先用time()给rand()种子
xxx.seed(rand()^time(NULL));//再用rand()给mt19937提供种子,这样生成的随机数质量更高一些
int w=xxx();//xxx()就是生成一个随机数
随机数。内容来自 https://www.cnblogs.com/sea-and-sky/p/18414461。
#include <bits/stdc++.h>
using namespace std;
const int N = 400010;
mt19937 rnd;
struct node {
int l, r;
int key, val;
int sz;
} a[N];
int n;
int rt, id;
int get(int x) {
a[++id] = {0, 0, x, rnd(), 1};
return id;
}
void pushup(int x) {
a[x].sz = a[a[x].l].sz + a[a[x].r].sz + 1;
}
void split(int p, int v, int &x, int &y) {
if (!p) {
x = y = 0;
return ;
}
if (a[p].key <= v)
x = p, split(a[x].r, v, a[x].r, y);
else
y = p, split(a[y].l, v, x, a[y].l);
pushup(p);
}
int merge(int x, int y) {
if (!x || !y)
return x + y;
if (a[x].val < a[y].val) {
a[x].r = merge(a[x].r, y), pushup(x);
return x;
}
a[y].l = merge(x, a[y].l), pushup(y);
return y;
}
void ins(int v) {
int x, y, z;
split(rt, v, x, y), z = get(v), rt = merge(merge(x, z), y);
}
void del(int v) {
int x, y, z;
split(rt, v, x, z), split(x, v - 1, x, y);
y = merge(a[y].l, a[y].r);
rt = merge(merge(x, y), z);
}
int get_k(int x, int k) {
if (k <= a[a[x].l].sz)
return get_k(a[x].l, k);
if (k == a[a[x].l].sz + 1)
return x;
return get_k(a[x].r, k - a[a[x].l].sz - 1);
}
int pre(int v) {
int x, y;
split(rt, v - 1, x, y);
int p = get_k(x, a[x].sz);
rt = merge(x, y);
return p;
}
int suf(int v) {
int x, y;
split(rt, v, x, y);
int p = get_k(y, 1);
rt = merge(x, y);
return p;
}
int get_rk(int v) {
int x, y;
split(rt, v - 1, x, y);
int k = a[x].sz + 1;
rt = merge(x, y);
return k;
}
int get_vl(int x) {
return a[get_k(rt, x)].key;
}
int main() {
srand(time(0));
rnd.seed(rand() ^time(0));
cin >> n;
while (n--) {
int op, x;
cin >> op >> x;
if (op == 1)
ins(x);
else if (op == 2)
del(x);
else if (op == 3)
cout << get_rk(x) << endl;
else if (op == 4)
cout << get_vl(x) << endl;
else if (op == 5)
cout << a[pre(x)].key << endl;
else
cout << a[suf(x)].key << endl;
}
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号