数学基础-概率论02 (连续型分布)
目录:
2.连续型
2.1 连续型均匀分布
一个均匀分布在区间[a,b]上的连续型随机变量X,可给出如下函数:
- $$f(n)= \begin{cases} {\frac{1}{b-a}}, & \text {for a <= x < b } \\ 0, & \text{elsewhere} \end{cases}$$
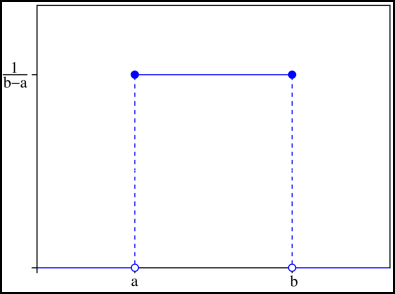
期望:$E[X]=\frac {a+b} 2$
方差:$V[X]=\frac {(b-a)^2} {12} $
特点:
均匀分布具有下属意义的等可能性。若 X ∼ U [a,b],则X落在[a,b]内任一子区间[c,d]上的概率:
$P(c \geq x \leq d) =F(d)-F(c)=\int_c^d \frac 1 {b-a} dx=\frac {d-c} {b-a}$
表示:只与区间[c,d]的长度有关,而与他的位置无关。
2.2 正态分布(高斯分布)
连续随机变量的概率密度函数是如下形式:
- $$f(x)=\frac{1}{σ \sqrt {2\pi} }e^{({-\frac{1}{2} {(\frac{x-μ}{σ}})^2})}$$
期望:$μ$
方差:$σ^2$
注:内容和离散型的正态分布基本一致,不再详细说明。
2.3 指数分布
指数分布是一种连续概率分布。指数分布可以用来表示独立随机事件发生的时间间隔,比如旅客进入机场的时间间隔、打进客服中心电话的时间间隔、中文维基百科新条目出现的时间间隔等等。
指数函数的一个重要特征是无记忆性,这表示如果一个随机变量呈指数分布,当s,t>0时有P(T>t+s|T>t)=P(T>s)。即,如果T是某一元件的寿命,已知元件使用了t小时,它总共使用至少s+t小时的条件概率,与从开始使用时算起它使用至少s小时的概率相等
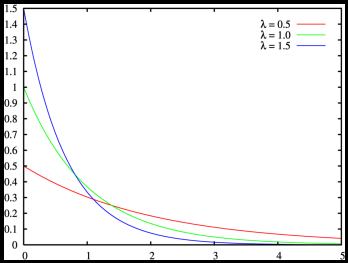
一个指数分布的概率密度函数是:
- $$f(x;\lambda )= \begin{cases} {\lambda e^{- \lambda x}}, & \text {x >= 0} \\ 0, & \text{x<0}\end{cases}$$
其中λ>0是分布的一个参数,常被称为率参数。即每单位时间发生该事件的次数。指数分布的区间是[0,∞)。 如果一个随机变量X 呈指数分布,则可以写作:X ~ Exponential(λ)
期望:$E(X)=\frac 1 {\lambda} $
方差:$V(X)=\frac 1 {\lambda^2}$
2.4 伽马分布
伽玛分布是统计学的一种连续概率函数。伽玛分布中的参数α,称为形状参数,β称为尺度参数。
令$X \sim \Gamma(\alpha,\beta)$;且令$\lambda=\frac 1 \beta$:即$X \sim \Gamma(\alpha,\frac 1 \lambda)$
假设随机变量X为 等到第α件事发生所需之等候时间, 分布函数为:
- $$f(x)=\frac {x^{\alpha - 1} \lambda^\alpha e^(-\lambda x)} \Gamma(a), \text x>0$$
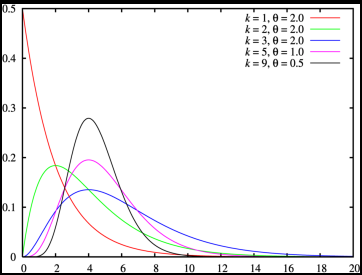
其中伽马(gamma)函数为:
- $$\Gamma(x)=\begin{cases} {(n-1)!} & \text {n为正整数} \\ \int_0^\infty{\frac {t^n-1} {e^t}dt} & \text{实步为正的虚数n} \end{cases}$$
伽马(gamma)函数具有以下性质:
- $$\begin{cases} {\Gamma(\alpha)=(\alpha-1)!}, & \text {if a is Z^+} \\ {\Gamma(\alpha)=(\alpha-1)\Gamma(\alpha-1)}, & \text{if a is }R^+ \\ \Gamma(\frac 1 2)=\sqrt \pi \end{cases}$$
期望:$ \mu=\frac \alpha \lambda$
方差:$V(X)=\frac \alpha {\lambda^2}$
特点:
当两随机变数服从Gamma分配,互相独立,且单位时间内频率相同时,Gamma分布具有加成性
- $$\prod=\begin{cases} {r.v.X \sim \Gamma(\alpha_1,\lambda)}\\ {r.v.X \sim >\Gamma(\alpha_2,\lambda}\end{cases} \implies X+Y \sim \Gamma(\alpha_1+\alpha_2,\lambda)$$
2.5 韦布尔分布
威布尔分布(Weibull distribution)是可靠性分析和寿命检验的理论基础。
例如,可以使用此分布回答以下问题:
- 预计将在老化期间失效的项目所占的百分比是多少?例如,预计将在8小时老化期间失效的保险丝占多大百分比?
- 预计在有效寿命阶段有多少次保修索赔?例如,在该轮胎的 50,000 英里有效寿命期间预计有多少次保修索赔?
- 预计何时会出现快速磨损?例如,应将维护定期安排在何时以防止发动机进入磨损阶段?
概率密度:
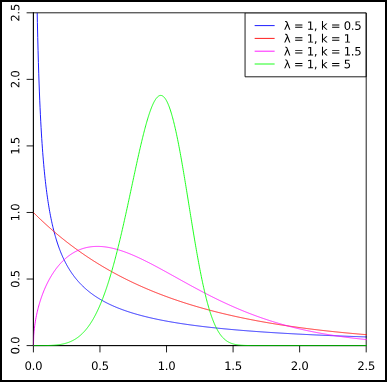
- $$f(x;\lambda,k)=\begin{cases} {\frac k \lambda(\frac x \lambda)^{k-1}e^{-(x/\lambda)^k}} & \text {x}\geq 0 \\ 0 & \text{x}\leq0 \end{cases}$$
其中,x是随机变量,λ>0是比例参数(scale parameter),k>0是形状参数(shape parameter)。显然,它的累积分布函数是扩展的指数分布函数,而且,Weibull distribution与很多分布都有关系。如,当k=1,它是指数分布;k=2时,是Rayleigh distribution(瑞利分布)
期望:$E=\lambda\Gamma(1+\frac 1 k)$
方差:$V=\lambda^2[\Gamma(1+\frac 2 k)-\Gamma(1+\frac 1 k )^2]$
注:$\Gamma$是伽玛函数
2.6 F分布
在概率论和统计学里,F-分布是一种连续概率分布,被广泛应用于似然比率检验.
概率密度函数:
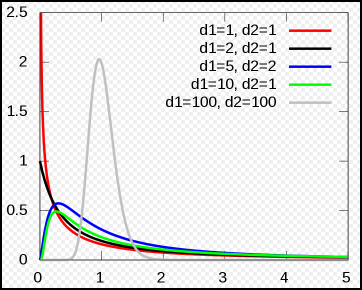
- $$f(x;d_1,d_2)=\frac {\sqrt{\frac {(d_1,x)^{d_1}{d_2}^d_2} {(d_1,x+d_2)^(d_1+d_2)}}} {x B(\frac {d_1} 2,\frac {d_2} 2)}$$
这里 B是B函数。在很多应用中,参数 d1 和 d2 是正整数,但对于这些参数为正实数时也有定义。
期望:$\frac{d_2}{d_2-2}, \text {for }d_2\geq2 $
方差:$\frac{2d_2^2(d_1+d_2-2)}{d_1(d_2-2)^2(d_2-4)}, \text {for }d_2\geq4 $
特点:
一个F-分布的随机变量是两个卡方分布变量除以自由度的比率:
- $$\frac{U_1/d_1}{U_2/d_2}=\frac{U_1/U_2}{d_1/d_2}$$
其中:
U1和U2呈卡方分布,它们的自由度(degree of freedom)分别是d1和d2。
U1和U2是相互独立的。
2.7 T分布
在概率论和统计学中,学生t-分布可简称为t分布,用于根据小样本来估计呈正态分布且方差未知的总体的均值。如果总体方差已知(例如在样本数量足够多时),则应该用正态分布来估计总体均值。它是对两个样本均值差异进行显著性测试的学生t检定的基础。
概率密度函数:
- $$f(t)=\frac{\Gamma(\frac{\nu+1}{2})}{\sqrt{\nu\pi}\Gamma(\frac \nu 2)}(1+\frac{t^2}{\nu})^{-\frac{\nu+1}{2}}$$
$\nu$等于n − 1。 T的分布称为t-分布。参数 $\nu$一般被称为自由度。
$\Gamma$是伽玛函数
期望:$\nu>1$时为0;$\nu=1$时未定义
方差:$\nu>2$时为$\frac \nu {\nu-2}$,否则无穷大
特点:
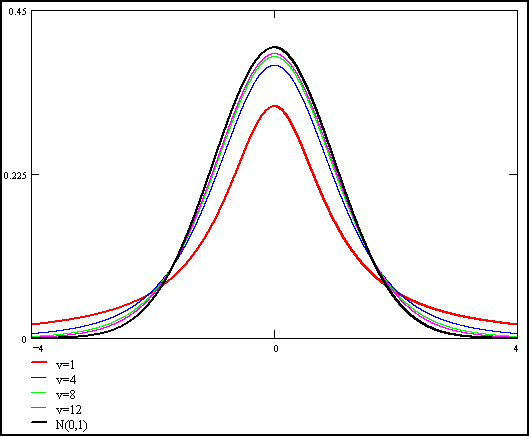
T的概率密度函数的形状类似于均值为0方差为1的正态分布,但更低更宽。随着自由度
$\nu$的增加,则越来越接近均值为0方差为1的正态分布。
2.8 贝塔分布
在概率论中,Β分布也称贝塔分布,是指一组定义在(0,1)区间的连续概率分布,有两个参数 α , β > 0.记为:$X\sim Be(\alpha,\beta)$.
B分布可以看做是分布之上的分布,当你不知道一个东西的具体概率是多少时,它可以给出了所有概率出现的可能性大小。
概率密度函数:
- $$f(x;\alpha,\beta)=\frac {x^{(\alpha-1)}(1-x)^{(\beta-1)}} {\int_0^1u^{\alpha-1}(1-u)^{\beta-1}du} $$
期望:$E=\frac{\alpha}{\alpha+\beta}$
方差:$V=\frac{\alpha\beta}{(\alpha+\beta)^2(\alpha+\beta+1)}$
详细资料参考:https://www.zhihu.com/question/30269898
2.9 卡方分布
卡方分布是概率论与统计学中常用的一种概率分布。k个独立的标准正态分布变量的平方和服从自由度为k的卡方分布,记为:$X\sim \chi^2(k) $
卡方分布是一种特殊的伽玛分布,是统计推断中应用最为广泛的概率分布之一,例如假设检验和置信区间的计算。
概率密度函数:
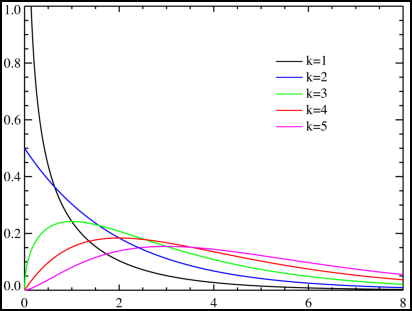
- $$f_k(x)=\frac{{\frac 1 2}^{\frac k 2}}{\Gamma(\frac k 2)}x^{\frac k 2 -1}e^{\frac{-x} 2}$$
其中x≥0,当x≤0时$f_k(x)=0$。这里Γ代表Gamma函数。
期望:k
方差:$\approx k(1-\frac{2}{9k})^3$
由卡方分布延伸出来皮尔森卡方检定常用于:
- 样本某性质的比例分布与总体理论分布的拟合优度(例如某行政机关男女比是否符合该机关所在城镇的男女比);
- 同一总体的两个随机变量是否独立(例如人的身高与交通违规的关联性);
- 二或多个总体同一属性的同素性检定(意大利面店和寿司店的营业额有没有差距)。(详见皮尔森卡方检定)
2.10 拉普拉斯分布
在概率论与统计学中,拉普拉斯分布(Laplace distribution)是以皮埃尔-西蒙·拉普拉斯的名字命名的一种连续概率分布。由于它可以看作是两个不同位置的指数分布背靠背拼接在一起,所以它也叫作双指数分布。
两个相互独立同概率分布指数随机变量之间的差别是按照指数分布的随机时间布朗运动,所以它遵循拉普拉斯分布。
概率密度函数:
- $$f(x|\mu,b)=\frac{1}{2}exp(-\frac{|x-\mu|}{b})=\frac{1}{2b}\begin{cases} exp(-\frac{\mu-x}{b}), & \text{if x<}\mu \\ exp(-\frac{x-}{b}), & \text{if x}\geq\mu \end{cases}$$
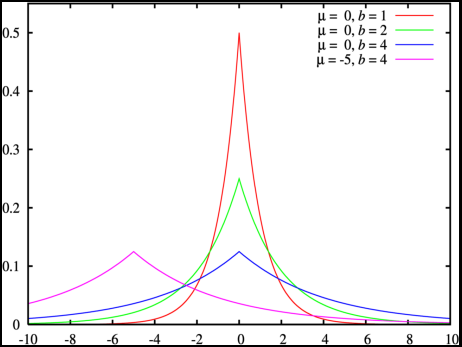
注:μ 是位置参数,b > 0 是尺度参数。如果 μ = 0,那么,正半部分恰好是尺度为 1/2 的指数分布。
期望:$\mu$
方差:$2b^2$
特点:
- 正态分布是用相对于 μ 平均值的差的平方来表示,而拉普拉斯概率密度用相对于平均值的差的绝对值来表示。因此,拉普拉斯分布的尾部比正态分布更加平坦
- 已知区间 (-1/2, 1/2] 中均匀分布上的随机变量 U,随机变量
$X=\mu-bsgn(U)ln(1-2|U|)$为参数 μ 与 b 的拉普拉斯分布


 浙公网安备 33010602011771号
浙公网安备 33010602011771号