PCA和LDA的对比

PCA和LDA都是经典的降维算法。PCA是无监督的，也就是训练样本不需要标签；LDA是有监督的，也就是训练样本需要标签。PCA是去除掉原始数据中冗余的维度，而LDA是寻找一个维度，使得原始数据在该维度上投影后不同类别的数据尽可能分离开来。

PCA

PCA是一种正交投影，它的思想是使得原始数据在投影子空间的各个维度的方差最大。假设我们要将N维的数据投影到M维的空间上（M<N），根据PCA，我们首先求出这N维数据的协方差矩阵，然后求出其前M个最大的特征值所对应的特征向量，那么这M个特征向量即为所求的投影空间的基。

LDA

用一句话来概括LDA的思想就是，投影后类内方差最小，类间方差最大。如下图所示有两种投影方式，左边的投影后红色数据和蓝色数据还有重叠部分，右边的投影后红色数据和蓝色数据则刚好被分开。LDA的投影即类似右边的投影方式，投影后使得不同类别的数据尽可能分开，而相同类别的数据则尽可能紧凑地分布。

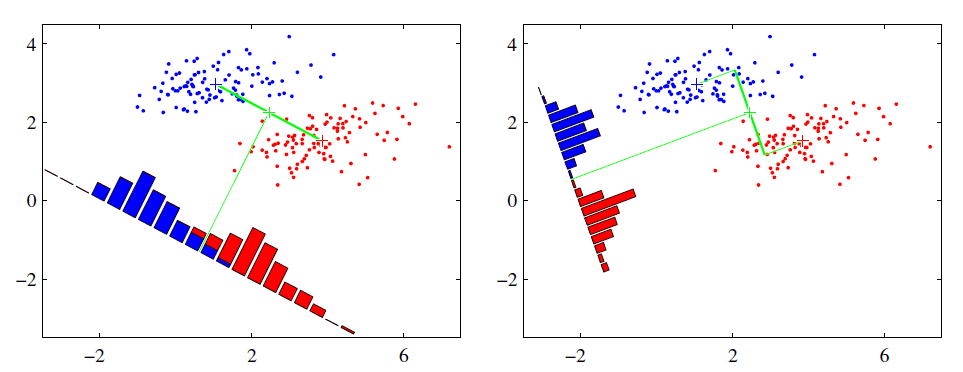
图片来源于网络

LDA的计算步骤：

1. 计算类间散度矩阵\(S_b\)

\[S_b=(\mu_0-\mu_1)(\mu_0-\mu_1)^T \]

其中\(\mu_0\)是第0类样本的均值，\(\mu_1\)是第1类样本的均值。
2. 计算类内散列矩阵\(S_w\)

\[S_w=\sum_{x\in X_0}(x-\mu_0)(x-\mu_1)^T+\sum_{x\in X_1}(x-\mu_1)(x-\mu_1)^T \]

其中\(X_0\)是第0类样本的集合，\(X_1\)是第1类样本的集合。
3. 求出最佳投影方向\(w\)，\(w\)即为\(S_w^{-1}S_b\)的最大特征值所对应的特征向量。

PCA和LDA的相同点

1. PCA和LDA都是经典的降维算法；
2. PCA和LDA都假设数据是符合高斯分布的；
3. PCA和LDA都利用了矩阵特征分解的思想。

PCA和LDA的不同点

1. PCA是无监督（训练样本无标签）的，LDA是有监督（训练样本有标签）的；
2. PCA是去掉原始数据冗余的维度，LDA是选择一个最佳的投影方向，使得投影后相同类别的数据分布紧凑，不同类别的数据尽量相互远离。
3. LDA最多可以降到k-1维（k是训练样本的类别数量，k-1是因为最后一维的均值可以由前面的k-1维的均值表示）；
4. LDA可能会过拟合数据。

Reference:

1. https://blog.csdn.net/yaoqi_isee/article/details/71036320
2. https://www.cnblogs.com/pinard/p/6244265.html