LeetCode 76. 最小覆盖子串

链接：leetcode acwing

暴力做法

问题的思考方式都是从暴力解法开始，然后再看看有没有什么性质可以利用来优化求解过程。这题很容易想到是两个问题的结合：枚举\(t\)的全排列以及匹配子序列。时间复杂度全排列是\(O(n!)\)的，是铁定会超时的。

滑动窗口（双指针）

当答案满足单调性时，就可以使用双指针算法。这题的单调性如下图所示，i右走，j不会左走.

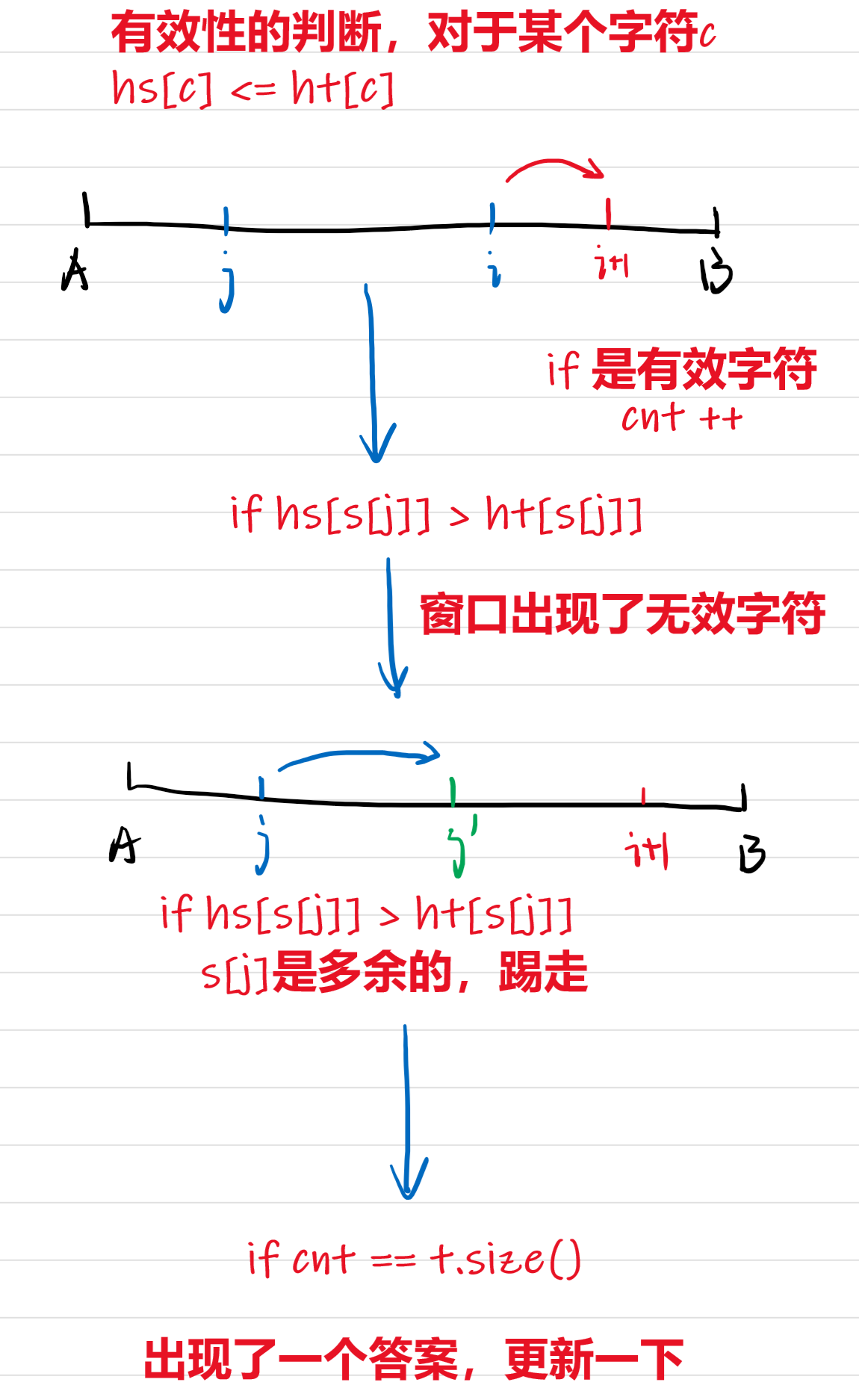
接下来一个问题，就是如何去获取T的某个排列是不是当前窗口的一个子序列。这里用的是哈希表。哈希表使得我们把用作比较的对象，不再是作为一个整体的字符串，而是一个个分散的字符，哈希表存储字符的数目，我们只要也统计当前窗口字符的数目，比较它们的数目即可。

接下来引入有效的概念，在统计的过程中，我们不是要做窗口每动一次就要遍历一遍统计各个字符数目。统计的过程和寻找答案的过程是相伴的。另外，比较两个哈希表之间是否相等，也不用线性遍历一下他们，我们可以使用cnt来统计当前窗口里真正有效的字符数量。窗口的哈希表各个字符的数目随着窗口变化也在变化，在变化的过程中一旦到了满足T的哈希表的时候，接下来的字符就不用再统计了，因为他们都是多余的了，也就是无效的。

保证了窗口哈希表存放的都是有效字符的数目，那么我们可以直接通过哈希表内的字符数目总值和T的长度来比较。

最后再看一下窗口的变化过程，窗口的右端向右移动，当cnt相等于T的长度，说明当前窗口已经能够涵盖T的所有字符。接下来就是再把左边界向右移动，直到把所有的无效字符踢出。我们就获得了一个（待定的）答案。在线性遍历的时候为何一下res就行。

class Solution {
public:
    string minWindow(string s, string t) {
        unordered_map<char, int> hs, ht;
        for (auto x : t) ht[x] ++;

        int cnt = 0;
        string res = "";
        for (int i = 0, j = 0; i < s.size(); i ++)
        {
            hs[s[i]] ++;
            if (hs[s[i]] <= ht[s[i]]) cnt ++;
            
            while(hs[s[j]] > ht[s[j]]) hs[s[j ++]] --;
            if (cnt == t.size())
            {
                if (res.empty() || res.size() > i - j + 1)
                    res = s.substr(j, i - j + 1);
            }
        }
        return res;
    }
};